П.1. Теоремы сложения вероятностей

Теорема 1.Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: Р(А+В)=Р(А)+Р(В).

Доказательство.

Докажем теорему для схемы случаев. Пусть всевозможные исходы опята сводятся к совокупности случаев, которые можно наглядно изобразить в виде n точек, из них m случаев благоприятствуют событию А, и k случаев благоприятствуют событию В. Тогда по определению вероятности 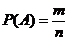, , 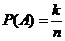так как А и В несовместны, то нет таких случаев, которые благоприятны А и В вместе. Следовательно, событию (А + В) благоприятны (m + k) случаев и 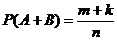. То есть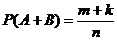 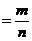+ 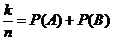, что и треб. доказать.

Теорема1^/(Обобщенная теорема сложения несовместных событий)Вероятность суммы n несовместных событий равна сумме вероятностей этих событий: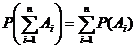

Доказательство (методом математической индукции).

Предположим, что теорема справедлива для (n-1) несовместного события: А₁, А₂,…,А_n-1, т.е. справедливо равенство: Р(А₁+ А₂+…+А_n-1)=Р(А₁)+Р(А₁₎ +…+ Р(А_n-1) . Докажем, что теорема будет справедлива для n несовместных событий.

Обозначим А₁+ А₂+…+А_n-1 =С.

Имеем Р(А₁+ А₂+…+А_n-1+ А_n) = Р(С + А_n) = (по теореме 1) = Р(С)+Р(А_n) = (а для (n-1) несовместного события теорема доказана) = Р(А₁+ А₂+…+А_n-1+ А_n)=Р(А₁)+Р(А₁₎ +…+ Р(А_n-1)+ Р(А_n).

(что и треб. доказать)

Следствие 1.Если событияА₁, А₂,…,А_n-1, А_n образуют полную группу несовместных событий, то сумма их вероятностей равна единице: .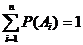

Доказательство.

Т.к. событияА₁, А₂,…,А_n-1, А_n образуют полную группу несовместных событий, то, по определению, появление хотя бы одного из них – достоверное событие:

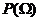= Р(А₁+ А₂+…+А_n-1+ А_n ) = 1.

Т.к. события несовместные, то к ним применима обобщенная теорема сложения:

Р(А₁+ А₂+…+А_n-1+ А_n )=Р(А₁)+Р(А₂) +…+ Р(А_n-1)+ Р(А_n) = 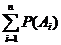=1, (что и треб. доказать).

Следствие 2. Сумма вероятностей противоположных событий равна единице: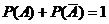

Доказательство.

События 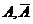– противоположные, т.е. по определению образуют полную группу несовместных событий, тогда по следствию 1, .

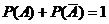Замечание.Следствие 2 – частный случай следствия 1. на практике весьма часто оказывается легче вычислить вероятность противоположного события, чем прямого.

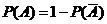
В формулировке таких задач встречаются слова «хотя бы», «не менее», «по крайней мере» и др.

Пример.Из колоды карт (36) наудачу вынимают 3 карты. Найти вероятность того, что среди них окажется хотя бы один туз.

Решение.

1 способ (по теореме ).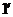

Событие А = {из 3 карт окажется хотя бы один туз}.

Хотя бы один – это либо один, либо два, либо три, т.е. событие А может быть представлено в виде суммы трех событий: А₁ = {из 3 карт окажется один туз}, А₂ = {из 3 карт окажется два туза}, А₃ = {из 3 карт окажется три туза}.

А = А₁+ А₂+А_3.

Т.к. события несовместны, то по теореме 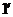: Р(А) = Р(А₁+ А₂+А₃)=Р(А₁)+Р(А₂) +Р(А₃).

Найдем отдельно вероятности событий.

, , .

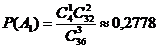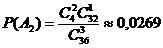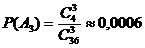Р(А) 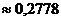+ 0,0269 + 0,0006 = 0,3053.

2 способ (по следствию 2).

Событие 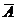= {из 3 вынутых карт не окажется ни одного туза}.

.

.

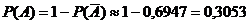Теорема 2.Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их произведения (совместного осуществления): Р(А+В)=Р(А)+Р(В) – Р(АВ)

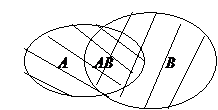Доказательство (геометрическое)

События отождествляют с множествами. Два раза накладываем «лепесток» друг на друга, поэтому и отнимаем его. (что и треб. доказать)

Теорема 2^/( Обобщенная теорема сложения совместных событий).

Вероятность суммы n совместных событий равна 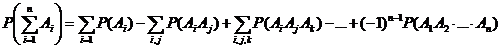, где суммы распространяются на различные значения индексов.

Для трех совместных событий теорема запишется в виде:

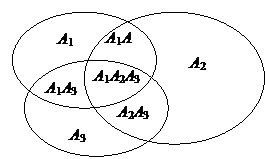Р(А₁+ А₂+А₃)=Р(А₁)+Р(А₂) +Р(А₃) – Р(А₁А₂) – Р(А₁А₃) – Р(А₂А₃) + Р(А₁А₂А₃)

Доказательство для трех событий (геометрическое):

События отождествляют с множествами (см. рис.).

(что и треб. доказать)

Замечание.Аналогичную формулу можно написать для произведения совместных событий:

Р(АВ) = Р(А)+Р(В) –Р(А+В)

Р(А₁А₂А₃) = Р(А₁)+Р(А₂) +Р(А₃) – Р(А₁+А₂) – Р(А₁ +А₃) – Р(А₂ +А₃) + Р(А₁+ А₂+А₃)

Пример.Для поражения самолета необходимо, чтобы были поражены оба двигателя (события А₁ и А₂) или была поражена кабина пилота (событие А₃). Требуется выразить вероятность поражения самолета (событие А) через вероятности событий А₁, А_2, А₃.

Решение.

А = А₁ А₂+А₃. Т.к. события совместны, то по теореме 2 следует, что

Р(А) = Р(А₁ А₂)+Р(А₃) – Р(А₁А₂А₃) = (по замечанию) = Р(А₁)+Р(А₂) – Р(А₁+А₂) – Р(А₁) –Р(А₂) – Р(А₃) + Р(А₁+А₂) + Р(А₁ +А₃) + Р(А₂ +А₃) – Р(А₁+ А₂+А₃) = – Р(А₃) + Р(А₁ +А₃) + Р(А₂ +А₃) – Р(А₁+ А₂+А₃) .