Свойства производной от дельта-функции

ДЕЛЬТА-ФУНКЦИЯ

Определение. Дельта-функция

,

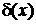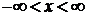
моделирует точечное возмущение и определяется в виде

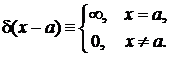(2.1)

Функция равна нулю во всех точках, кроме 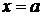, где ее аргумент равен нулю, и где функция бесконечная, как показано на рис. 1,а. Задание 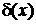значениями в точках аргумента неоднозначно из-за ее обращения в бесконечность, поэтому дельта-функция является обобщенной функцией, и требует доопределения в виде нормировки.

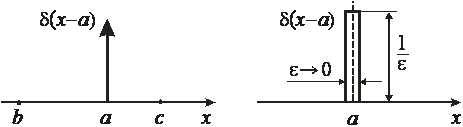
а б

Рис.1. Дельта-функция

Условие нормировки

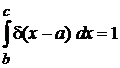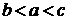, . (2.2)

Площадь под графиком функции равна единице в любом интервале, содержащем точку a, как показано на рис 1,б. Поэтому дельта-функция моделирует точечное возмущение единичной величины.

Четность функции следует из (2.1)

,

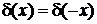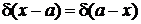. (2.2а)

Из симметрии 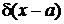относительно точки 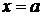получаем

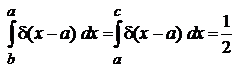, (2.2б)

как следует из рис 1,б.

Ортонормированность. Множество функций

, ,

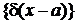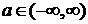образует ортонормированный бесконечномерный базис.

Дельта-функцию применил в оптике Кирхгоф в 1882 г., в электромагнитной теории – Хевисайд в 90-х годах XIX в.

Густав Кирхгоф (1824–1887) Оливер Хевисайд (1850–1925)

Оливер Хевисайд – ученый самоучка, впервые использовал в физике векторы, разработал векторный анализ, ввел понятие оператора и разработал операционное исчисление – операторный метод решения дифференциальных уравнений. Ввел функцию включения, названную позже его именем, использовал точечную импульсную функцию – дельта-функцию. Применил комплексные числа в теории электрических цепей. Впервые записал уравнения Максвелла в виде 4-х равенств вместо 20 уравнений, как было у Максвелла. Ввел термины: проводимость, импеданс, индуктивность, электрет. Разработал теорию телеграфной связи на большие расстояния, предсказал наличие у Земли ионосферы – слой Кеннелли–Хевисайда.

Математическую теорию обобщенных функций разработал Сергей Львович Соболев в 1936 г. Он был одним из основателей Новосибирского Академгородка. Его именем назван Институт математики СО РАН.

Сергей Львович Соболев (1908–1989)

Свойства ДЕЛЬТА-ФУНКЦИИ

Фильтрующее свойство

Для гладкой функции , не имеющей разрывов, из (2.1)

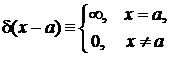
получаем

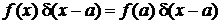. (2.3)

Полагая 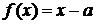, и используя дельта-функцию в виде предела при 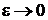, показанного на рис. 1,б, находим

,

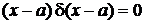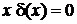. (2.4)

Интегрирование 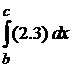дает фильтрующее свойство в интегральной форме

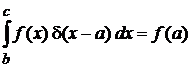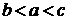, . (2.5)

Ортонормированность базиса

В (2.5) полагаем

, ,

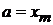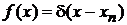и получаем условие ортонормированности базиса с непрерывным спектром

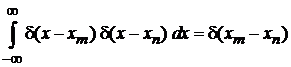. (2.7)

Масштабное преобразование аргумента

Выполняется

,

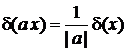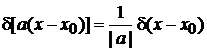, (2.8)

Доказательство

Интегрируем произведение дельта функции с гладкой функцией 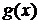по интервалу 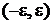, где :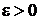

,

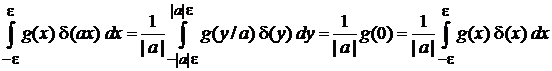где сделана замена переменной 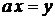и использовано фильтрующее свойство 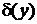. Сравнение начального и конечного выражений дает (2.8).

Упрощение аргумента

Если 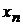– корни функции 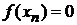, тогда

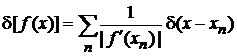. (2.9)

Доказательство

Функция отлична от нуля только вблизи точек 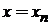, в этих точках она бесконечна.

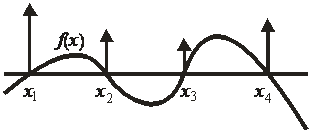
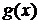Для нахождения веса, с которым входит бесконечность, интегрируем произведение с гладкой функцией по интервалу 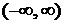. Не равны нулю вклады только в окрестности точек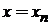

.

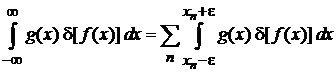В малой окрестности 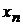разлагаем в ряд Тейлора

,

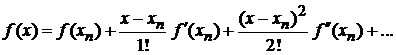и ограничиваемся первыми двумя слагаемыми

.

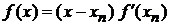Используем (2.8)

,

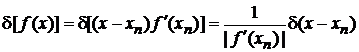тогда

.

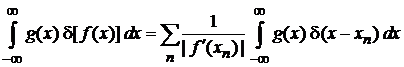Сравниваем подынтегральные функции и получаем (2.9).

Свертка

Из определения свертки (1.22)

,

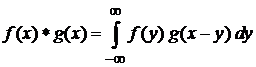при 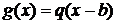получаем

.

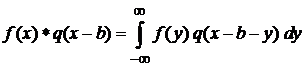Полагаем 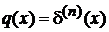, и находим

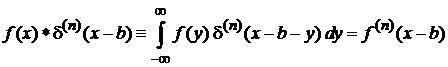, (2.14)

где использовано (2.13).

Интегральное представление

Выполняется

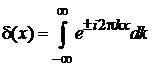. (2.24)

Доказательство

Вычисляем

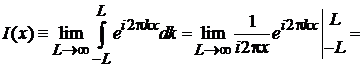
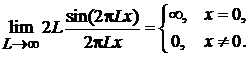
Учтено, что при 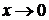и конечном L

.

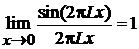При 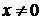функция 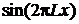с ростом L колеблется около нуля с частотой пропорциональной L, и ее среднее значение равно нулю.

Функция 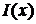удовлетворяет нормировке

,

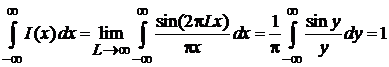где сделана замена 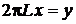. Выполнены условия (2.1) и (2.2), следовательно, .

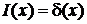Выполняется

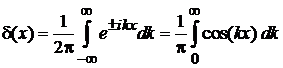. (2.24а)

Доказательство

Используем (2.24)

,

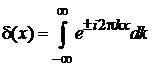заменяем 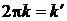и получаем первое равенство (2.24а).

По формуле Эйлера

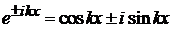
получаем второе равенство (2.24а).

Дифференцируем (2.24)

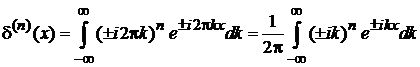. (2.25)

Выражения в виде пределов

При выводе (2.24) получено

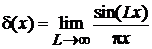. (2.29)

Выполняется

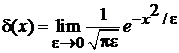, (2.30)

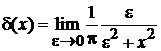. (2.33)

Фурье-образ

Из (1.1)

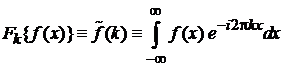
и фильтрующего свойства (2.5)

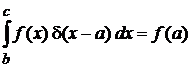
находим

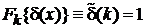. (2.35а)

Теорема Фурье о смещении аргумента

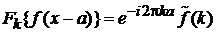
и (2.35а) дают

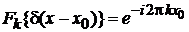. (2.35б)

Из (1.1) и интегрального представления (2.24)

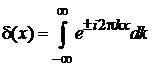
получаем

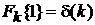. (2.36а)

Теорема Фурье о фазовом сдвиге функции

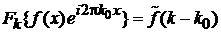
и (2.36а) дают

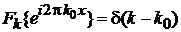. (2.36б)

Из (2.35а) и теоремы Фурье о дифференцировании

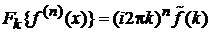
находим

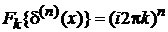. (2.37а)

Из (2.36а) и теоремы Фурье об умножении на аргумент

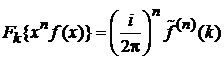
получаем

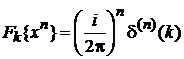. (2.37б)

Гребенчатая функция

(2.53)

Моделирует неограниченную кристаллическую решетку, антенну и другие периодические структуры.

При Фурье-преобразовании гребенчатая функция переходит в гребенчатую функцию.

Из (2.53)

,

с учетом

(2.8)

получаем

. (2.54)

Свойства

Функция четная

,

периодическая

,

период . Фильтрующее свойство дельта-функций дает

. (2.55)

Фурье-образ

Для периодической функции с периодом L Фурье-образ выражается через коэффициенты Фурье

, (1.47)

, (1.49)

Для гребенчатой функции с периодом получаем

,

где учтено фильтрующее свойство дельта-функции. Из (1.47) находим Фурье-образ

. (2.56)

Фурье-образом гребенчатой функции является гребенчатая функция.

Из (2.56) по теореме Фурье о масштабном преобразовании аргумента получаем

. (2.59)

Увеличение периода гребенчатой функции ( ) уменьшает период и увеличивает амплитуду ее спектра.

Ряд Фурье

Используем

, (1.48)

.

Для , получаем

. (2.57)

ДЕЛЬТА-ФУНКЦИЯ

Определение. Дельта-функция

,

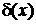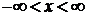
моделирует точечное возмущение и определяется в виде

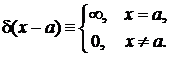(2.1)

Функция равна нулю во всех точках, кроме 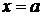, где ее аргумент равен нулю, и где функция бесконечная, как показано на рис. 1,а. Задание 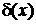значениями в точках аргумента неоднозначно из-за ее обращения в бесконечность, поэтому дельта-функция является обобщенной функцией, и требует доопределения в виде нормировки.

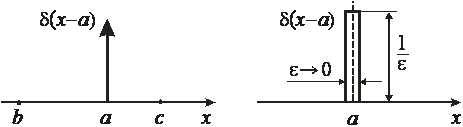
а б

Рис.1. Дельта-функция

Условие нормировки

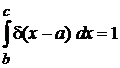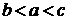, . (2.2)

Площадь под графиком функции равна единице в любом интервале, содержащем точку a, как показано на рис 1,б. Поэтому дельта-функция моделирует точечное возмущение единичной величины.

Четность функции следует из (2.1)

,

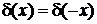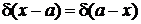. (2.2а)

Из симметрии 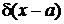относительно точки 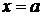получаем

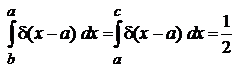, (2.2б)

как следует из рис 1,б.

Ортонормированность. Множество функций

, ,

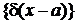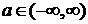образует ортонормированный бесконечномерный базис.

Дельта-функцию применил в оптике Кирхгоф в 1882 г., в электромагнитной теории – Хевисайд в 90-х годах XIX в.

Густав Кирхгоф (1824–1887) Оливер Хевисайд (1850–1925)

Оливер Хевисайд – ученый самоучка, впервые использовал в физике векторы, разработал векторный анализ, ввел понятие оператора и разработал операционное исчисление – операторный метод решения дифференциальных уравнений. Ввел функцию включения, названную позже его именем, использовал точечную импульсную функцию – дельта-функцию. Применил комплексные числа в теории электрических цепей. Впервые записал уравнения Максвелла в виде 4-х равенств вместо 20 уравнений, как было у Максвелла. Ввел термины: проводимость, импеданс, индуктивность, электрет. Разработал теорию телеграфной связи на большие расстояния, предсказал наличие у Земли ионосферы – слой Кеннелли–Хевисайда.

Математическую теорию обобщенных функций разработал Сергей Львович Соболев в 1936 г. Он был одним из основателей Новосибирского Академгородка. Его именем назван Институт математики СО РАН.

Сергей Львович Соболев (1908–1989)

Свойства ДЕЛЬТА-ФУНКЦИИ

Фильтрующее свойство

Для гладкой функции , не имеющей разрывов, из (2.1)

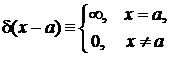
получаем

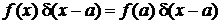. (2.3)

Полагая 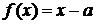, и используя дельта-функцию в виде предела при 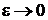, показанного на рис. 1,б, находим

,

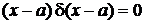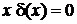. (2.4)

Интегрирование 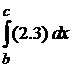дает фильтрующее свойство в интегральной форме

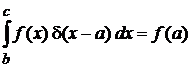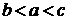, . (2.5)

Ортонормированность базиса

В (2.5) полагаем

, ,

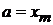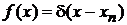и получаем условие ортонормированности базиса с непрерывным спектром

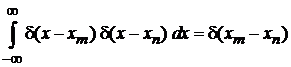. (2.7)

Масштабное преобразование аргумента

Выполняется

,

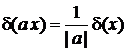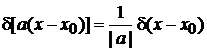, (2.8)

Доказательство

Интегрируем произведение дельта функции с гладкой функцией 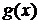по интервалу 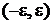, где :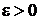

,

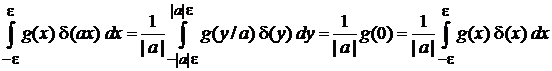где сделана замена переменной 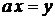и использовано фильтрующее свойство 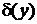. Сравнение начального и конечного выражений дает (2.8).

Упрощение аргумента

Если 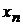– корни функции 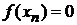, тогда

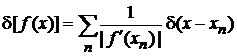. (2.9)

Доказательство

Функция отлична от нуля только вблизи точек 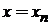, в этих точках она бесконечна.

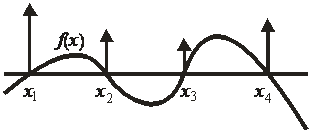
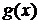Для нахождения веса, с которым входит бесконечность, интегрируем произведение с гладкой функцией по интервалу 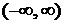. Не равны нулю вклады только в окрестности точек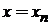

.

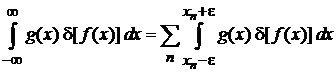В малой окрестности 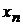разлагаем в ряд Тейлора

,

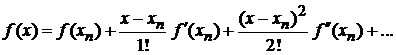и ограничиваемся первыми двумя слагаемыми

.

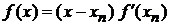Используем (2.8)

,

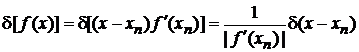тогда

.

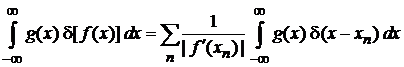Сравниваем подынтегральные функции и получаем (2.9).

Свойства производной от дельта-функции

Четность. Из (2.2а)

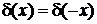
получаем

,

,

,

.

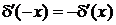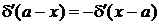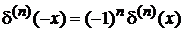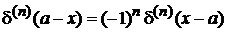Фильтрующее свойство. Выполняется

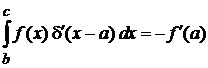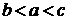, , (2.10)

Доказательство

Интегрируем (2.10) по частям, используя

,

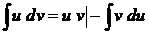где

, ,

, .

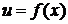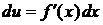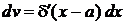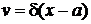Получаем

,

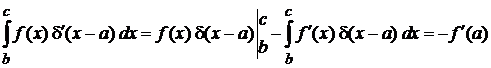где учтено .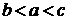

Доказать самостоятельно:

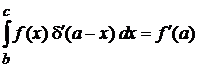, (2.11)

,

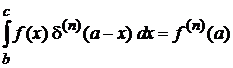. (2.13)

Свертка

Из определения свертки (1.22)

,

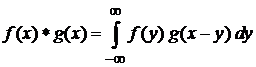при 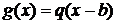получаем

.

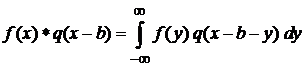Полагаем 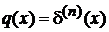, и находим

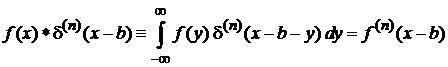, (2.14)

где использовано (2.13).

Интегральное представление

Выполняется

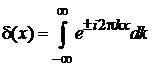. (2.24)

Доказательство

Вычисляем

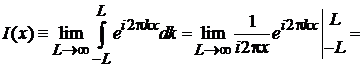
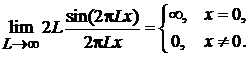
Учтено, что при 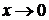и конечном L

.

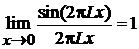При 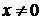функция 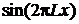с ростом L колеблется около нуля с частотой пропорциональной L, и ее среднее значение равно нулю.

Функция 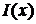удовлетворяет нормировке

,

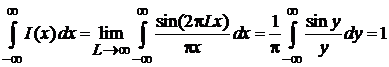где сделана замена 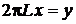. Выполнены условия (2.1) и (2.2), следовательно, .

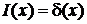Выполняется

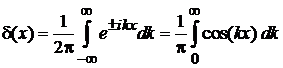. (2.24а)

Доказательство

Используем (2.24)

,

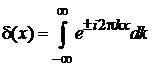заменяем 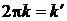и получаем первое равенство (2.24а).

По формуле Эйлера

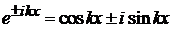
получаем второе равенство (2.24а).

Дифференцируем (2.24)

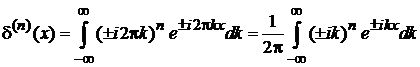. (2.25)

Выражения в виде пределов

При выводе (2.24) получено

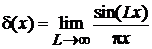. (2.29)

Выполняется

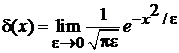, (2.30)

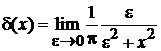. (2.33)

Фурье-образ

Из (1.1)

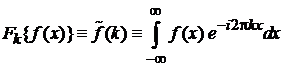
и фильтрующего свойства (2.5)

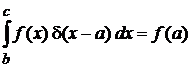
находим

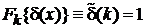. (2.35а)

Теорема Фурье о смещении аргумента

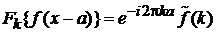
и (2.35а) дают

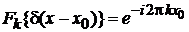. (2.35б)

Из (1.1) и интегрального представления (2.24)

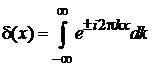
получаем

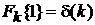. (2.36а)

Теорема Фурье о фазовом сдвиге функции

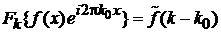
и (2.36а) дают

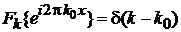. (2.36б)

Из (2.35а) и теоремы Фурье о дифференцировании

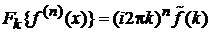
находим

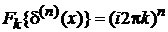. (2.37а)

Из (2.36а) и теоремы Фурье об умножении на аргумент

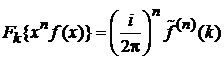
получаем

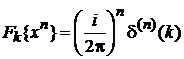. (2.37б)