Дифференцирование неявных функций.

Дифференцирование неявной функции

Функция z = ƒ (х; у) называется неявной, если она задается уравнением

неразрешенным относительно z. Найдем частные производные 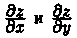неявной функции z, заданной уравнением (44.11). Для этого, подставив в уравнение вместо z функцию ƒ (х; у), получим тождество F(x;у;ƒ (х; у)) = 0. Частные производные по х и по у функции, тождественно равной нулю, также равны нулю:

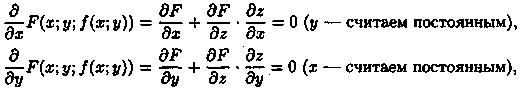
откуда

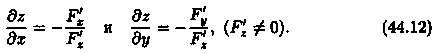
61. Экстремум функции двух переменных

Говорят, что функция 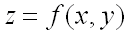имеет максимум в точке 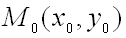, т.е. при 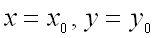, если 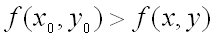для всех точек 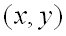, достаточно близких к точке 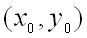и отличных от неё.

Говорят, что функция 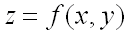имеет минимум в точке 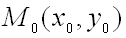, т.е. при 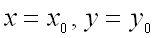, если 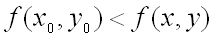для всех точек 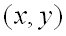, достаточно близких к точке 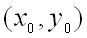и отличных от неё.

Максимум и минимум функции называются экстремумами функции.

Теорема (необходимое условие экстремума функции двух переменных). Если функция 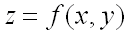достигает экстремума при 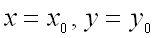, то каждая частная производная первого порядка от 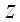или обращается в нуль при этих значениях аргументов, или не существует.

Теорема (достаточное условие экстремума функции двух переменных). Пусть в некоторой области, содержащей точку 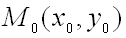функция 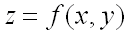имеет непрерывные частные производные до третьего порядка включительно. Пусть, кроме того, точка 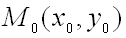является критической точкой функции 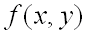, т.е.
,
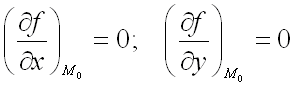тогда при :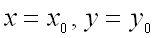
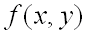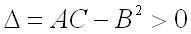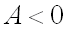1) имеет максимум, если дискриминант и , где ;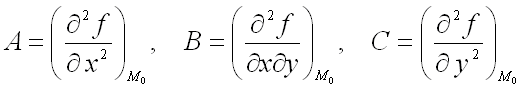
2) 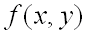имеет минимум, если дискриминант 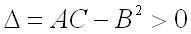и ;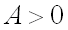
3) 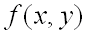не имеет ни минимума, ни максимума, если дискриминант ;
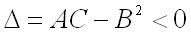4) если 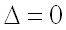, то экстремум может быть, а может и не быть (требуется дополнительное исследование).

Метод наименьших квадратов.

Такая модель в общем виде может быть представлена уравнением (1.2):

y_t = a₀ + a₁ х_1t +...+ a_n х_nt + ε_t .

Исходными данными при оценке параметров a₀ , a₁ ,..., a_n является вектор значений зависимой переменной y = (y₁ , y₂ , ... , y_T)' и матрица значений независимых переменных

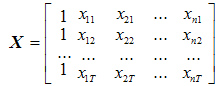
в которой первый столбец, состоящий из единиц, соответствует коэффициенту модели .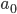

Название свое метод наименьших квадратов получил, исходя из основного принципа, которому должны удовлетворять полученные на его основе оценки параметров: сумма квадратов ошибки модели должна быть минимальной.

63. Производная по направлению.

Производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления.

Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению.

Рассмотрим функцию 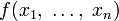от 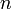аргументов в окрестности точки 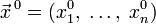. Для любого единичного вектора 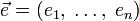определим производную функции 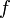в точке 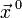по направлению 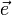следующим образом:

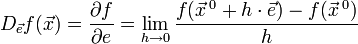
Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора .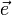

Если направление сонаправленно с координатной осью, то производная по направлению совпадает с частной производной по этой координате.

Градиент.

Градиент — характеристика, показывающая направление наискорейшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой. Например, если взять высоту поверхности Земли над уровнем моря (2-мерное пространство), то её градиент в каждой точке поверхности будет показывать «в горку».

Как видно из объяснения, градиент является векторной функцией, а величина, которую он характеризует — функцией скалярной.Формально, для случая трёхмерного пространства, градиентом называется векторная функция с компонентами 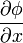, , 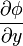, 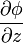где φ — некоторая скалярная функция координат x, y, z.

Если φ — функция n переменных 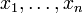, то её градиентом будет n-мерный вектор

,

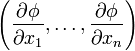компоненты которого равны частным производным φ по всем её аргументам.

Градиент обозначается gradφ или, с использованием оператора набла, .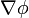

Из определения градиента следует, что:

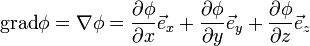
Свойства:

§

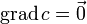
Линейность

§

§

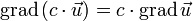
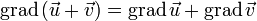
Правило Лейбница

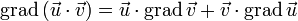§ , где 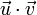— скалярное произведение векторов 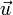и .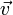

Связь с градиентом:Производную по направлению дифференциируемой по совокупности переменных функции можно рассматривать как проекцию градиента функции на это направление, или иначе, как скалярное произведение градиента на орт направления:

,

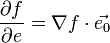где 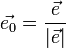— орт направления. Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлением градиента функции в данной точке. Также видно, что значение производной по направлению не зависит от длины вектора .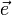