Математическое понятие поля. Градиент

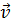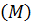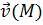2.1. Скалярное поле и градиент. Под математическим полем понимают пространство (неограниченное или только область), каждой точке которого сопоставляется значение некоторой величины: скаляра ψ или вектора ; соответственно различают скалярные и векторные поля. Подчеркивая пространственную зависимость, пишут ψ и , где подразумевается точка наблюдения М, либо 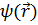и 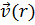, поскольку точка М вполне характерируется своим радиус-вектором 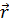. Мы будем часто пользоваться декартовыми координатами и писать ψ(x,у,z) и 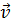(x, у, z), полагая, что эти функции обладают требуемыми аналитическими свойствами (I.5 п. 1).

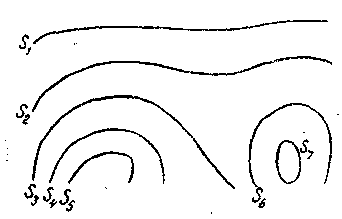
Рис. 2.1

Наглядный образ скалярного поля очень прост. Если, в частности, скалярная функция 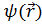положительна, то её можно принять за плотность какого-то условного вещества и мысленно выделить сгустки и разрежения последнего. В общем случае в скалярном поле возможно выделить геометрические места точек, в которых функция 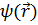принимает те или иные постоянные значения. Это так называемые поверхности уровня; на рис. 2.1 показан пример сечения (плоскостью чертежа) системы поверхностей уровня. Каждая из поверхностей, следы которых видны на рис. 2.1, описывается в декартовых координатах уравнением

ψ(х, у, z) = С_i, (2.1)

где C_i -константа, своя для данной поверхности уровня S_i. Очевидно также, что

dψ = 0 на S_i, (2.1а)

где подразумевается дифференциал функции ψ(х, у, z) при перемещении точки М на S_i.

Рассмотрим две достаточно близкие поверхности уровня и выделим малую область поля, в которой участки этих поверхностей с нужной степенью точности неотличимы от параллельных плоскостей. Пусть разность значений функции 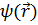, принимаемых ею на выделенных поверхностях уровня, равна Δψ. На рис. 2.2, где следы этих поверхностей показаны в виде двух прямых, построены также два направления: нормаль к поверхностям и некоторое произвольное направление 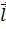. Поскольку расстояние между поверхностями по нормали - кратчайшее и Δn = Δlcos 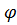, то, составив отношения Δψ/Δν и Δψ/Δl, отмечаем, что

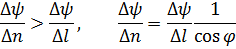
Предельные формы этих соотношений, возникающие при сближении поверхностей уровня, отличаются только тем, что отношения приращений переходят в частные производные. Таким образом (для дифференцируемых ψ):

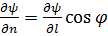(2.2)

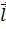Δn

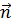φ

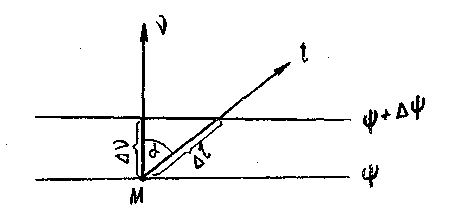
Рис. 2.2

и, следовательно, среди производных функции 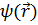, по всевозможным направлениям, производная по нормали к поверхности уровня является максимальной. Вектор, направленный в сторону наибольшего изменения ψ и равный по абсолютному значению его скорости, называется градиентом ψ и обозначается grad ψ. Согласно предыдущему

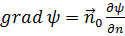, (2.3)

где 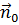- единичный вектор нормали .

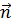2.2. Градиент в декартовых координатах.Желая выразить векторную функцию grad ψ в заданной декартовой системе координат, рассмотрим сначала проекцию этого вектора на произвольно выделенное направление 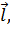обозначаемую grad_lψ. По определению проекции,

,

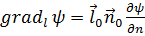где 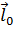- единичный вектор вдоль 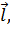а поскольку 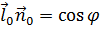(см. рис. 2.2), то согласно (2.2)

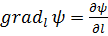. (2.4)

В качестве 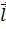можно взять направление х, у или z; частными формами (2.4) являются, таким образом, равенства:

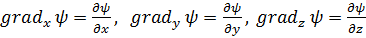. (2.4a)

Отсюда получаем:

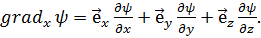(2.5)

где 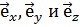- единичные векторы координатных осей.

Итак, исходя из произвольного cкалярного поля, мы получили векторную функцию координат 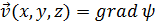, и имеем теперь определённого типа векторное поле.

2.3. Векторное поле и силовые линии. Векторные поля наглядно изображаются при помощи силовых линий. Это такие линии, которые в каждой точке указывают направление векторной функции своей касательной. Отдельная силовая линия не даёт информации об абсолютном значении векторной функции, но картины силовых линий стараются строить так, чтобы об интенсивности поля можно было судить по их густоте.

Введём понятие векторного дифференциала длины вдоль некоторой линии:

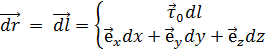(2.6)

В первой строчке он выражен через обычный дифференциал длины и единичный вектор касательной 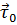, а во второй - через дифференциалы и единичные векторы декартовых координат.

Пусть задана векторная функция 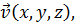и соответствующее векторное поле описывается силовыми линиями. Будем считать, что есть векторный дифференциал силовой линии; тогда он везде параллелен вектору

,

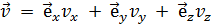т. е. (k - коэффициент пропорциональности). Сравнивая представления 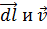в декартовых координатах, получаем пропорцию

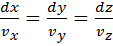, (2.7)

из которой следуют дифференциальные уравнения, характеризующие силовые линии.

2.4. Потенциальные векторные поля. Вернёмся к векторному полю, полученному в п. 2. Если задана векторная функция, которую теперь обозначим 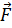, являющаяся градиентом некоторой скалярной функции ψ, то соответствующее векторное поле называется потенциальным, а ψ - потенциалом. Поверхности уровня, на которых ψ = const, являются, следовательно, поверхностями постоянного потенциала, или эквипотенциальными поверхностями. Легко сообразить, что линии вектора 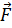= grad ψ должны быть ортогональны эквипотенциальным поверхностям, т. е. пересекать их под прямым углом. Это проверяется, например, следующим образом. Возьмем элементарное смещение в виде дифференциала 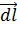, перпендикулярное вектору 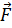. Это значит, что равно нулю скалярное произведение 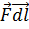, т. е. согласно (2.5) и (2,6)

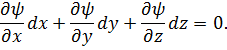
Слева стоит полный дифференциал функции ψ; таким образом, получено равенство dψ = 0,совпадающее с (2.1а) и описывающее эквипотенциальную поверхность. На последней, как видим, и лежит ортогональный градиенту 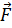элемент .

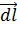Заметим, что для данного 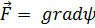потенциал ψ определён лишь с точностью до постоянного слагаемого, поскольку gradψ = grad(ψ + const).

Введём в рассмотрение следующий важный интеграл

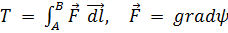. (2.8)

Это криволинейный интеграл, вычисляемый вдоль некоторого пути по кривой l от точки А до точки В. Если 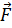- сила, то записанный интеграл выражает совершаемую на данном пути работу. Подынтегральное выражение 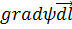можно записать также в форме .

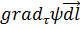Раскрывая скалярное произведение 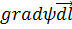на основании (2.5) и (2.6) подобно тому, как это уже делалось, имеем:

,

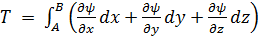или

.

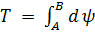Поэтому

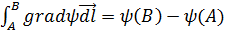, (2.9)

т. е. интеграл Т (2.8) при однозначности ψ не зависит от пути, а определяется только значениями потенциала ψ в начальной и конечной точках пути. Иными словами, каков бы ни был путь интегрирования, ведущий от точки А к точке В, значение Т остается равным разности потенциалов в этих точках.

Далее из (2.9) следует, что интеграл типа (2.8) по замкнутому пути L равен нулю:

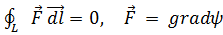, (2.10)

поскольку точки А и В в данном случае совпадают. Интеграл (2.10) называется циркуляциейвектора F по замкнутому пути L. Согласно полученному результату, циркуляция градиента тождественно равна нулю.

2.5. Пример градиента.При изучении различных полей важную роль играет обратная величина расстояния между точками, определяемая согласно (1.16а) как

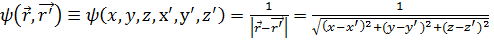. (2.11)

Фиксируя точку Р(х', у', z'), будем рассматривать эту величину как функцию ψ(x, у, z) и вычислим её градиент gradψ. Пользуясь формулами (2.4а), (2.5), находим:

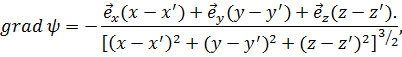
или

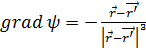(2.12)

В частности, когда точка Р(х' у', z') совпадает с началом координат О(0, 0, 0), т. е. 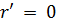, имеем:

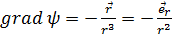(2.12а)

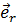( - орт радиального направления ).

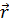Если же фиксирована точка М(х, у, z), то 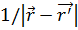есть функция ψ(x', у', z'). Градиент этой функции 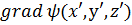,обозначаемый также grad'ψ, вычисляется по формулам (2.4а), (2.5) при замене д/дх на д/дх'и т. д. В результате вместо (2.12)получаем:

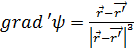(2.13)

В том случае, когда фиксированная точка М(х, у, z)совпадает с началом координат О(0, 0, 0), т. е. r = 0:

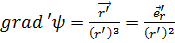,(2.13а)