Понятие о поверхностях 2го порядка.

Алгебраическим ур-ем 2ой степени наз.

ур-е вида Ax²+Bxy+Cy²+Dx+ey+F=0,

где A,B,C,D,e,F - действительные числа

Линии, которые в системе декартовых

координат определяются алгебраическим

ур-ем 2ой степени наз. линиями 2го порядка.

Опред/ пределов последовательности

И ф-ции. Осн. св-ва пределов ф-ции

Ой переменной.

а) Предел последовательности:

y=f(Un), где U₁,U₂,...U_n, а U_n=n/(n²+1)

Предел: число а называется пределом

переменной x_n, если для каждого “+” как

угодно малого числа e(эпсилон) существует

такой номер N,

что при n>N разность |x_n-a|<e

limx_n=a

n®¥

-e<X_n-a<e

a-e<X_n<a+e

б) Предел ф-ции:
y=f(x) число а называется пределом

переменной х, если разность м/ду ними

есть б.м.в. |x-a|®0, |x-a|<e

Число А называется пределом ф-ции f(x)

при х®а, если для каждого, как угодно малого

на период заданного числа e. -e>0, найдется

такое как угодно малое на период заданного

d>0, что будут выполняться неравенства:

Если |x-a|<d, то |f(x)-A|<e

Основные св-ва:
1.Если величина имеет предел, то только 1.

2. limC=C, где С- постоянная величина

3. Если a-б.м.в., то lima=0

4. предела б.б.в. не существует

5. если limy=a, то y=a+a, где a-б.м.в.

Основные теоремы о пределах.

1. Предел суммы = суммы пределов:
limx=a, limy=b, тогда x=a+a, y=b+b, где a и

b - б.м.в. x+y=(a+a)+(b+b)=(a+b)+(a+b),

где a+b=w- б.м.в.

x±y=(a±b)+w, то lim(x±y)=a±b=limx+limy.

2. Теорема о пределе производной: если

сомножители имеют пределы, то и

произведение имеет предел, равный

произведению пределов сомножителей.

limx=a, limy=b, то на основании 5го св-ва

x=a+a

y=b+b, где a и b - б.м.в.

x*y=(a+a)*(b+b)=a*b+(ab+ab+ab), то

­сумма б.м.в. = d(дельта)

xy=ab+d

xy®ab,

limxy=ab=limx*limy

3. Следствие: постоянная величина

выноситься за знак предела.

limCx=limC*limx=C*limx

4. Предел от частного = частному

пределов (кроме limx/limy=0

limx/y=limx/limy, т.к. limx=a, limy=b

x=a+a, y=b+b

x/y=(a+a)/(b+b)

Й, 2й замечательный пределы.

1й: limsinx/x=1, limx/sinx=1.

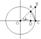x®0

j

lim((Sina)/a)=1

x®0

S_DOAC<S_{сектораOAC}<S_DOCB

S_DOAC=1/2*OC*AD,

OA=OC=1, то

S_DOAC=1/2*OC*OA*Sina=1/2*Sina

S_{сектораOAC}=1/2*OA*OC*a=1/2*a(т.к. OA=OC)

S_DOCB=1/2*OC*BC=1/2*OC*OC*tga=1/2*tga

1/2*Sina<1/2*a<1/2tga //*2

sina<a<tga//:sin

1<a/sina<1/cosa, =>cosa<sina/a<1,

limCosa<lim((Sina)/a)<lim1, по признаку

a®0 a®0 существования

предела ф-ции

lim((Sina)/a)=1

a®0

2ой: lim(1+1/n)ⁿ=e»2.7183

n®¥

Зная, что 1/n=a - б.м.в., то n=1/a и

x®¥ a®0

lim(1+1/n)^1/a=e

a®0

Основные приемы нахождения пределов.

1. Подстановка: при х®х₀ и х₀Îобласти

определения ф-ции f(x), предел ф-ции f(x)= его

частному значению при х=х₀

limf(x)=f(x₀)

x®x₀

2. Сокращение: при х®¥ и х®х₀ f(x)/g(x)=0/0, то

сокращают числитель и знаменатель на

множитель, стремящийся к 0.

3. уничтожение иррациональности

(* числитель и знаменатель на 1 число).

4.деление на наивысшую степень х:

при х®¥ и х®х₀ f(x)/g(x)=0/0, то делим

числитель и знаменатель на наивысшую cтепень.

5. сведение к известным пределам: lim((Sinx)/x)=1

x®¥

lim(1+1/n)^x=e

x®¥

Непрерывность ф-ции в точке

И на интервале.

x=x₀+Dx, Dx=x-x₀

Dy=f(x₀+Dx)-f(x₀)

Ф-ция y=f(x) наз. непрерывной

в точке x₀, если она определена

в окрестности этой точки,

а limDy=0. (б.м. приращению аргумента

соответствует б.м. приращению ф-ции).

limDy=lim[f(x)-f(x₀)]=limf(x)-limf(x₀)=0, то

limf(x)=limf(x₀)

x®x₀

Ф-ция непрерывна в точке х₀, если

ее предел = значению этой ф-ции в точке х₀

Ф-ция явл. непрерывной на интервале,

если она непрерывна в каждой его точке.

Признаки существования а) предела ф-ции и

б) предела последовательности.

а) если все значения ф-ции f(x) заключены

между значениями ф-ции j(x) и g(x), которые

имеют 1 предел при х®а, то и limf(x)=A

j(x)<=f(x)<=g(x), где limj(x)=А, limg(x)=А,

то limf(x)=A. х®а

б) Если последовательность монотонно

возрастает и ограниченна сверху, то она

имеет предел.

Последовательность монотонно возрастает,

если последующий член>предыдущего (x_n+1>x_n)

Последовательность ограничена сверху,

если существует такое М, что x_n<=M.

Бесконечно малые величины и их св-ва:

величина называется б.м.в. в каком-то процессе,

если она в этом процессе бесконечно

уменьщается.

(r=m/V, если V®¥, то r®0)

Св-ва б.м.в.:

-сумма или разность конечного числа б.м.в. есть

б.м.в.

(a и b-б.м.в., то a±b=б.м.в.)

-произведение б.м.в. на величину ограниченную

есть б.м.в. (U<=M, то a*U=б.м.в.)

-произведение б.м.величин=б.м.в.

-произведение б.м.в. на постоянную = б.м.в