Однородные системы линейных уравнений и их решение

МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ

Прямоугольная таблица, составленная из m x n элементов aij (i = 1,m, j -1,n) некоторого множества, называется матрицей и записывается в виде

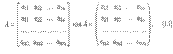
Элементы матрицы нумеруются 2 индексами. Первый индекс i эле­мента aij обозначает номер строки, а второй j — номер столбца, на пе­ресечении которых находится этот элемент в матрице. Матрицы обычно обозначают прописными буквами латинского алфавита: А, В, С,.. . Если у матрицы m строк и n столбцов, то по определению она имеет раз­мерность m x n. В случае необходимости это обозначается следующим образом:

Аm x n. Матрица называется числовой, если ее элементы aij — числа; функциональной, если aij — функции; векторной, если aij — век­торы, и т.д. Матрицы А и В называются равными, если все их соот­ветствующие элементы aij и bij равны, т.е. aij = bij. Следовательно, равными могут быть только матрицы одинаковой размерности. Матри­цы, у которых т = п, называются квадратными. Если i -1, то получаем матрицу-строку; если j =1, имеем матрицу-столбец. Их также называют вектор-строкой и вектор-столбцом соответственно.

Перечислим основные операции над матрицами.

1. Сложение и вычитание матриц. Эти операции определяются только для матриц одинаковой размерности. Суммой (разностью) ма­триц А и В, обозначаемой А + В (А — В), называется матрица С, эле­менты которой Cij == aij =b bij, где aij и bij — соответственно элементы матриц А и В. Например, пусть

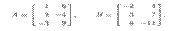
Тогда

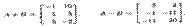
2. Умножение матрицы на число. Произведением матрицы А и числа А, обозначаемым А А, называется матрица В той же размерности, элементы которой bij = Аа^, где aij — элементы матрицы А, т. е. при умножении матрицы на число (числа на матрицу) надо все элементы матрицы умножить на это число. Например, пусть

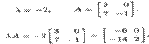
3. Умножение матриц. Произведением матриц Am x n и Bn x p на­зывается матрица

Сm x p = А • В (или проще АВ), элементы которой Cij = ∑ⁿ_k=1 aikbkj, где aik>bkj — элементы матриц А и В. Отсюда следует, что произведение АВ существует только в случае, когда первый
множитель А имеет число столбцов, равное числу строк второго множи­теля В. Далее, число строк матрицы АВ равно числу строк А, а число столбцов — числу столбцов В. Из существования произведения АВ не следует существование произведения ВА. В случае его существования, как правило, ВА≠АВ. Если АВ — В А, то матрицы А и В называются перестановочными (или коммутирующими). Известно, что всегда (АВ)С = А(ВС).

ОПРЕДЕЛИТЕЛИ И ИХ СВОЙСТВА.

ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ

Определителем n-гo порядка называется число ∆n, записываемое в виде квадратной таблицы

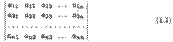
и вычисляемое, согласно указанному ниже правилу, по заданным чис­лам aij (i,j = 1, n), которые называются элементами определителя (всего их n²). Индекс i указывает номер строки, aj — номер столбца квадратной таблицы (1.1), на пересечении которых находится элемент aij. Любую строку или столбец этой таблицы будем называть рядом.

Главной диагональю определителя называется совокупность элемен­тов

a_11, a_{22,… .} Минором Mij элемента aij называется определитель (n — l)-гo по­рядка ∆n-i, полученный из определителя n-гo порядка ∆n вычеркива­нием г-й строки и j-гo столбца.

Алгебраическое дополнение Aij элемента aij определяется равен­ством

Aij = (-l)^i+j Mij

Значение определителя ∆n находится по следующему правилу.

Для n = 2

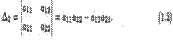
Для n = 3

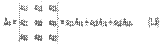
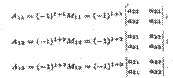
Величины A₁₁,A₁₂,A₁₃ — алгебраические дополнения, а M₁₁,M₁₂, M₃₃ — миноры определителя ∆з, соответствующие его элементам a₁₁, a₂₂,a₃₃. Эти миноры являются определителями второго порядка, полу­чаемыми из определителя ∆з вычеркиванием соответствующих строки и столбца. Например, чтобы найти минор Mi2, следует в определителе ∆з вычеркнуть первую строку и второй столбец. Для произвольного n

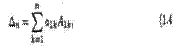
где A_1k = (-l)^1+M_1k а миноры M_1k, являющиеся определителями (n - l)-гo порядка, получаются из ∆n вычеркиванием первой строки и k−го столбца. Например,

Замечание. Если элементами определителя являются некоторые функции, то данный определитель, вообще говоря, тоже функция (но может быть и числом). Например,

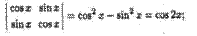
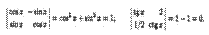
Правило вычисления определителя ∆з равносильно правилу тре­угольников (правилу Cappюca):

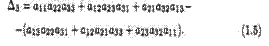
Схематическая запись этого правила приведена ниже:

Например,

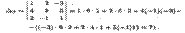
Перечислим основные свойства определителей:

1) сумма произведений элементов любого ряда определителя и их алгебраических дополнений не зависит от номера ряда и равна этому определителю:

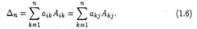
Эти равенства можно было бы (как и формулу (1.4)) принять за правило

вычисления определителя. Первое из них называется разложением ∆∏ по элементам %-й строки, а второе — разложением ∆n по элементам j-гo столбца;

2) значение определителя не меняется после замены всех его строк соответствующими столбцами, и наоборот;

3) если поменять местами два параллельных ряда определителя, то он изменит знак на противоположный;

4) определитель с двумя одинаковыми параллельными рядами равен нулю;

5) если все элементы некоторого ряда определителя имеют общий множитель, то последний можно вынести за знак

определителя. Отсюда следует, что если элементы какого-либо ряда умножить на число λ, то определитель ∆n умножится на это же число λ;

6) если все элементы какого-либо ряда определителя равны нулю, то определитель также равен нулю;

7) определитель, у которого элементы двух параллельных рядов со­ответственно пропорциональны, равен нулю;

8) сумма всех произведений элементов какого-либо ряда определи­теля и алгебраических дополнений соответствующих элементов другого параллельного ряда равна нулю, т. е. верны равенства:

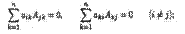
9) если каждый элемент какого-либо ряда определителя представля­ет собой сумму двух слагаемых, то такой определитель равен сумме двух определителей, в первом из которых соответствующий ряд состоит из первых слагаемых, а во втором — из вторых слагаемых:

Например,

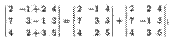
10) определитель не изменится, если ко всем элементам какого-либо его ряда прибавить соответствующие элементы другого параллельного ряда, умноженные на одно и то же произвольное число Л. Например, для столбцов определителя это свойство выражается равенством

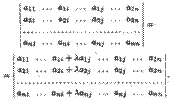
Рассмотрим основные методы вычисления определителей.

1. Метод эффективного понижения порядка. В соответствии со свойством 4 вычисление определителя n-гo порядка сводится к вычисле­нию n определителей (n - l)-гo порядка. Этот метод понижения порядка не эффективен. Используя основные свойства определителей, вычисле­ние ∆n ≠ 0 всегда можно свести к вычислению одного определителя (n — l)-гo порядка, сделав в каком-либо ряду ∆n все элементы, кроме одного, равными нулю, покажем это на примере. Пример 1. Вычислить определитель

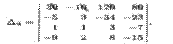
► ∏о свойству 5 определителей из первой строки вынесем множитель 10, а затем будем последовательно умножать полученную строку на 3, 1, 2 и складывать соответственно со второй, третьей и четвертой строками. Тогда, согласно свойству 10, имеем:

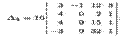
∏о свойству 1 определителей (см. второе из равенств (1.6)) полу­ченный определитель молено разложить по элементам второго столбца. Тогда

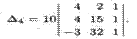
Получили определитель третьего порядка, который молено вычис­лить по правилу Cappюca или подобным же приемом свести к вычисле­нию одного определителя второго порядка. Действительно, вычитая из второй и третьей строк данного определителя первую строку, получаем:

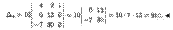
2. Приведение определителя к треугольному виду. Определитель, у которого все элементы, находящиеся выше или ниже главной диагонали, равны нулю, называется определителем треугольного вида. Очевидно, что в этом случае определитель равен произведению элементов его глав­ной диагонали. Приведение любого определителя ∆n к треугольному виду всегда возможно.

Пример 2. Вычислить определитель

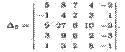
► Выполним следующие операции. Пятый столбец определителя сло­жим с первым, этот же столбец, умноженный на 3, — со вторым, на 2 — с третьим, на 8 — с четвертым столбцом. В итоге получим определитель треугольного вида, который равен исходному:

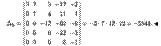
Приведение определителей к треугольному виду будет использовать­ся в дальнейшем при решении систем линейных уравнений методом Жopдaнa — Гаусса (его называют также методом Гаусса).

Метод Гаусса

2-этапа

1 Прямой ход Гаусса: последовательное исключение неизвестных из систем испозуются 3 преобразования оставляющие систему эквивалентнай

-перестановка местами уравнений

-умножение обеих частей урав. На произвольное число не=0

-прибавление к уравнению другого уравн. Умноженного на произвольное число

2 Обратный ход : находим неизвестные системы.

Если к системе прибавить свободный член то матрица называется расшыренной

Прямой ход Гаусса удобно проводить с расшыренной матрицей, работая только со строками.

Матрица приводится к трапецевидному виду в результате Прямого хода Гаусса

следующие вариант

в последнем ходе уравнения остается одна неизвестная – система имеет одно решение.

в последнем ходе уравнения остается две или более неизвестных – система имеет бесконечное множество решений.

Кривизна

,

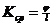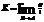
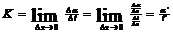
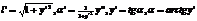
Получаем:

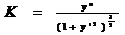
Радиус кривизны- величина обратная кривизне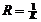

Геометрическое место центра кривизны есть кривая наз. эволютой.

№ 21 Расстояние точки до пл-ти.

y-y₀=k(x-x₀)- уравненіе прямой проходяўей через точку x_0,y₀

№22 Виды прямой в пространстве. Угол между прямыми, усл. параллельности и перпендикулярности.

tgφ/k2-k1/1+k1k2

k1=k2- условие параллельности

k1k2= -1 условие перпендикулярности

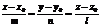- каноническое уравнение прямой

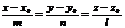- параметрические уравнение

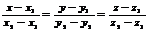- Ур-ние прямой проход. через 2 заданные точки

Линии второго порядка

Линией (кривой) второго порядка наз множество М точек плоскости, координаты х,у которых удовлетворяют алгебраическому уравнению второй степени.

(1)Ах²+Ву²+Сху+Дх+Еу+F=0 Для того, чтобы определить тип линий второго порядка, ее параметры и построить график необходимо уравнение (1) привести к каноническому виду. Если в уравнении (1) отсутствует слагаемое Сху, то оно приводится к кананическому виду выделением полного квадрата.

Частные случаи уравнения:

1. эллипс- множество точек в плоскости, каждая из которых удовлетворяет следующему условию: сумма расстояния от точки эллипса до двух данных точек наз фокусами есть величина постоянно большая чем расстояние между фокусами. Уравнение эллипса предполагает, что его фокусы лежат на оси.

х²/а²+у²/в²=1 – каноническое уравнение эллипса.

а,в- полуоси эллипса , в- меньшая полуось, а- большая

в= √а² -с²

эксцентриситет:

Е= 2с/2а=с/а, Е<1

Если центр эллипса нах в произвольной точке М(х,у,), то тогда уравнение эллипса имеет след вид (х-х´²)/а²+(у-у´²)/в²=1

2. Гипербола- множество точек в плоскости для каждой из которой выполняется условие: разность параллельных расстояний от точки гиперболы до 2 данных точек наз фокусами, есть величина постоянная < чем расстояние между фокусами.

х²/а²-у²/в²=1 – каноническое уравнение гиперболы с фокусами на ОХ

а- действительная полуось, в- мнимая в=√с²-а²

асимптотами гиперболы явл 2 симметричные ей прямые

у= ±(в/а)х

эксцентриситет:

Е= 2с/2а=с/а, Е>1

Если фокусы лежат на оси ОУ: х²/а²-у²/в²=-1

Соотношение между осями: в=√с²-а²

Если центр симметрии гиперболы нах в начале координат а,в произвольной точке М (х,у) то: (х-х´²)/а²+(у-у´²)/в²=±1

3. парабола – множество точек в плоскости каждая из которых равно удалена от заданной точки наз фокусами данной прямой наз директрисой.

у²= 2рх кананическое уравнение параболы с фокусами на ОХ, р- параметр параболы

х=-р/2- директриса

F(р/2;0)

Фокус на оси ОУ х²= 2ру

F(0;р/2) у= -р/2

Если вершина параболы находится в точке М(х,у) то уравнение параболы записывается:

(у-у´)²= 2р(х-х´)

(х-х´)²= 2р(у-у´)

Алгебра производных

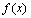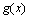Выведем важнейшие формулы, касающиеся вычисления производных. В дальнейшем и - некоторые функции, у которых существуют 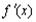и 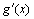, а C - некоторая константа (число).

1.

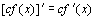
Доказательство

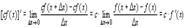
2.

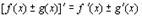
Доказательство

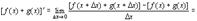
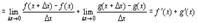
Аналогично выводится формула для .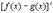

3.

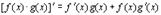
Доказательство

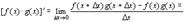
В числителе дроби прибавим и вычтем комбинацию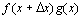

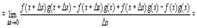
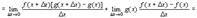
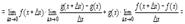
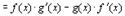
4.

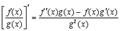
Доказательство

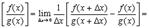
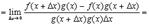
прибавляем и вычитаем в числителе комбинацию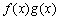

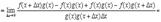
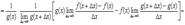
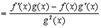
5.

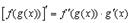
В выражении 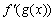подразумевается, что производная от функции 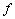берется так, как будто 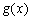является единым целым (аргументом).

Доказательство

Пусть аргумент 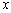получил приращение 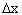. Тогда функция > 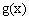получила приращение 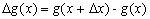так что 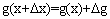. Поэтому

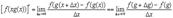
делим и умножаем дробь на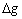

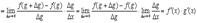
6.

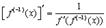
Доказательство

Пусть 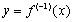так что 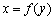. Если аргументу x дать приращение 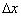то величина 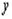получит приращение 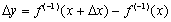. Поэтому

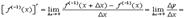
Однако в данной формуле есть одна неувязка. Слева стоит функция от 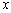, а справа получилась функция от 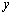. Чтобы устранить это несоответствие надо в правой части заменить 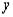на 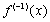. Тогда получим окончательно

.

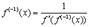7.

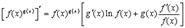
Вывод этой формулы следует разбирать после прочтения следующего параграфа.

Доказательство

Обозначим 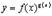. Тогда 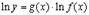. Вычисляя производную от обеих частей этого равенства, получим

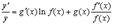
Отсюда

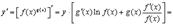
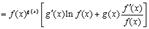
Вместо того чтобы запоминать эту формулу лучше запомнить правило: для того чтобы вычислить производную от 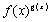, надо это выражение сначала прологарифмировать.

Все эти формулы сведены в следующую таблицу, которую следует запомнить (кроме последней формулы).

Функция	Производная

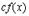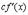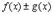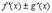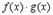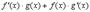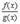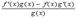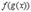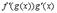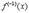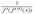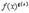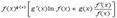Таблица производных

Выведем теперь таблицу производных от элементарных функций

1.

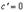
Действительно, если 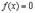, то

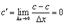
2.

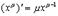
Имеем

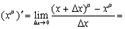
вынесем вверху 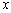за скобки

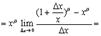
Сделаем “замену переменных” 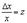. Тогда 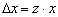и

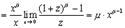
Так как мы получили один из замечательных пределов. Рекомендуется запомнить некоторые частные случаи этой функции этой формулы

а)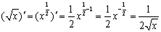

б)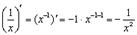

3.

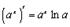
Имеем

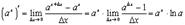
так как мы снова имеем один из замечательных пределов.

Особенно простой результат получается при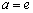

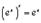
4.

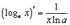
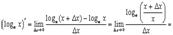
сделаем “замену переменных” 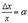. Тогда 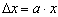и

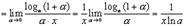
Особенно простой результат получается при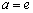

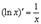
5.

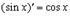
Имеем

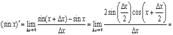
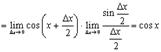
где так же использован замечательный предел.

6.

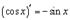
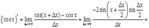
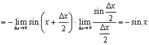
7.

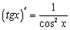
Так как 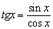, то

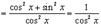
8.

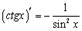
Вывод аналогичен

9.

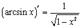
В данном случае 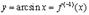и 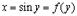, т.е. 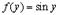. Поэтому

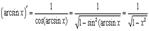
10.

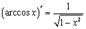
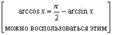
Вывод аналогичен

11.

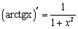
В данном случае 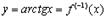и 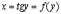, т.е. 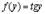. Поэтому

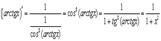
12.

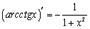
Вывод аналогичен

13.

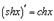
Действительно

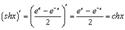
14. 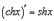15.

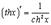
Вывод аналогичен

Особые случаи

То, что в точке 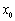функция 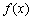непрерывна не означает, разумеется, что в этой точке у нее обязательно существует производная. Функция может быть непрерывной, а производной может и не существовать. Что же там может быть?

1. А. Односторонние производные

Назовем

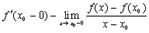
производной от функции 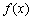в точке 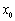слева, а

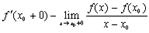
производной в той же точке справа. Разумеется, если 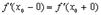, то это означает, что в точке 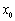существует 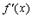. Но могут быть случаи, когда 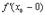и 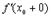существуют, но не равны друг другу. В этом случае не существует и 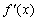. График функции 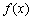имеет в точке 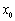в этом случае “излом”, и в этой точке к графику можно провести две касательные .

2. Б. Бесконечная производная

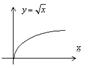
Рассмотрим функцию 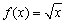определенную для 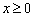и потребуем найти 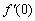. Имеем

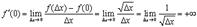
и производная равна .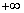

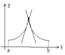
Рассматривая график функции 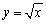легко увидеть, что это означает просто то, что в точке 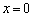касательная к графику параллельна оси OY.

3. В. Несуществование производной

Наконец, может быть ситуация, когда , фигурирующий в определении производной, не существует.

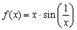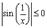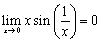Рассмотрим для примера, . Так как , то . Поэтому полагая 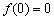получим

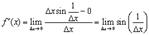
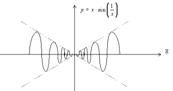
и этот предел просто не существует.

Из графика функции 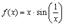видно, что с приближением к точке 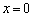касательная колеблется, не стремясь ни к какому определенному положению.

В математике построены даже примеры функций, которые являются непрерывными, но ни в одной точке не имеют производной.

Теоремы Ферма и Ролля

Теорема Ферма. Пусть функция 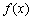определена и непрерывна на промежутке 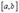и в некоторой внутренней точке 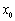этого промежутка достигает своего наибольшего или наименьшего значения, если в этой точке существует производная, то она равна нулю: .

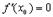Доказательство

Пусть, для определенности, в точке 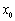функция 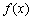достигает своего наибольшего.

По условию теоремы эта точка внутренняя, т.е. 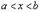, и поэтому к этой точке можно подойти и слева и справа.

Пусть мы подходим к 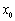слева. Тогда

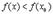(т.к. 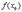- наибольшее значение)

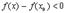
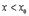(т.к. мы подходим слева)

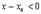
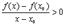
Делая предельный переход 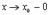получим

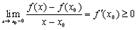
Пусть мы подходим к точке 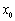справа. Тогда

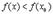(т.к. 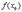- наибольшее значение)

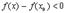
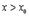(т.к. мы подходим слева)

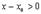
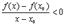
Делая предельный переход 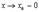получим

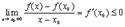
Совместить два полученных неравенства можно только в одном случае: 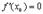. ч.т.д.

Геометрический смысл доказанной теоремы ясен из рисунка: в точке наибольшего или наименьшего значения функции касательная к графику функции параллельна оси OX.

1. Существование ограничений

В теореме Ферма по сути дела два ограничения: а) точка 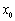расположена внутри отрезка 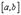и б) 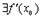. Покажем, что оба ограничения являются существенными, т.е. отказ от любого из них приводит к тому, что утверждение теоремы становится неверным.

а) “внутренность” точки x₀

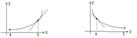
Если максимум или минимум функции 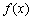достигается на границе отрезка, то утверждение теоремы Ферма неверно. При доказательстве это проявляется в том, что мы сможем подойти к точке 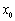только с одной стороны и поэтому не получится второго, противоположного неравенства.

б) существование производной.

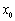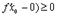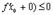Пусть в точке существуют только односторонние производные. Тогда, как это видно из рисунка, теорема Ферма неверна. При доказательстве это проявиться в том, что получаться неравенства и , которые нельзя будет объединить в одно равенство, т.к. теперь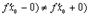

Теорема Ролля. Пусть функция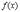

а) определена и непрерывна на [a,b]

б) ;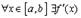

в)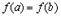

Тогда существует точка 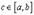в которой .

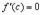Доказательство этой теоремы следует из такой логической цепочки рассуждений:

1. Так как 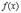определена и непрерывна на 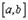, то, по первой теореме Вейерштрасса, она ограничена на 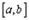, т.е. существуют конечные 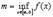и .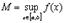

2. Если 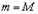, то 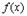есть константа, т.е. 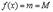и поэтому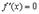 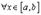. В качестве точки c можно взять любую точку из .

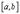3. Если 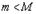, то, в силу условия 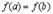и второй теоремы Вейерштрасса, хотя бы одно из значени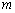й или 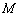достигается во внутренней точке промежутка 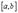,по теореме Ферма, в этой точке (их может быть и две) производная равна нулю.

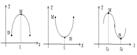
ч.т.д.

Формулы Коши и Лагранжа

Теорема. Пусть функци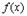и и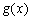

а) определены и непрерывны на ;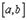

б) 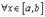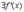и ;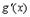

в)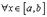

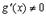
Тогда существует точка 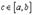такая, что

.

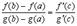Эта формула носит название формулы Коши.

Доказательство. Прежде всего отметим, что 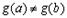, иначе, по Теореме Ролля, существовала бы точка 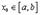, где 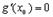, что противоречит ограничению “в”.

Рассмотрим функцию

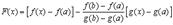
Она

а) определена и непрерывна на 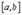, т.к. 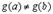и функци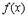и и 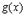непрерывны на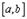

б)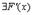

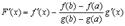
в)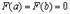

Таким образом, для 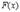выполнены все условия Теоремы Ролля. Поэтому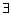 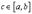такая, что

,

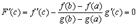но тогда в этой точке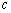

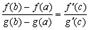
что и дает формулу Коши.

1. Формула Лагранжа

Рассмотри частный случай, когда 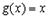. Тогда формула Коши приобретает вид

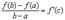
или

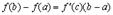
где 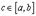. Эта формула и называется формулой Лагранжа. В дальнейшем мы будем на нее часто ссылаться.

Заметим, что точка c не обязательно единственная: может быть несколько точек c, удовлетворяющих формулам Коши или Лагранжа.

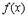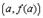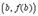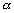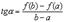Рассмотрим еще вопрос о геометрическом смысле формулы Лагранжа. Пусть мы имеем график . Проведем через точки и секущую. Она образует с осью OX угол и . Но 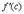есть тангенс угла, который касательная к кривой в точке 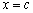образует с осью OX. Поэтому формулу Лагранжа можно трактовать так: существует точка 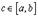, касательная в которой параллельна секущей, соединяющей точк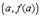и и .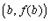

Дифференциал

Рассмотрим важное для дальнейшего понятие дифференциала.

Напомним, что величина 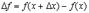называется приращением функции.

Определение 1. Функция 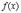называется дифференцируемой в точке 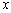, если ее приращение можно представить в виде

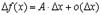
Определение 2. Линейная часть приращения функции, т.е. 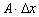называется дифференциалом функции 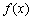и обозначается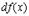

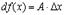
Чтобы точно уяснить эти определения функции рассмотрим пример. Пусть 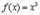. Тогда

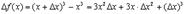
Заметим, что 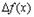содержит слагаемое, линейное по 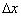, слагаемые с 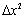и