Теорема 4 (второй признак экстремума функции).

Пусть 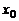– критическая точка функции 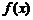, дважды дифференцируемой в окрестности точки 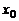. Тогда 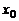является точкой локального минимума функции 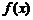, если 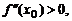и точкой локального максимума, если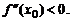

Теорема 5 (Вейерштрасса). Если функция 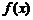непрерывна на отрезке 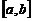, то она достигает на нем своих наименьшего и наибольшего значений

Непрерывная на отрезке 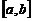достигает наименьшего (наибольшего) значений либо на концах отрезка, либо в точках ее локального экстремума.

Для отыскания глобальных экстремумов функции 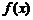на отрезке 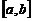необходимо:

1) найти производную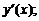

2) найти критические точки функции;

3) найти значения функции на концах отрезка, т. е. 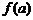и 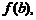а также в критических точках, принадлежащих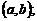

4) из всех полученных значений функции определить наибольшее и наименьшее ее значения.

Теорема о выпуклости графиков.Если функция f(x) дважды дифференцируема в окрестности точки x0 и вторая производная строго меньше нуля, то график функции выпуклый, а если больше нуля, то – вогнутый.

Точка графика функции, в которой выпуклость сменяется вогнутостью (и наоборот) называется точкой перегиба.

Асимптотойк графику функции y = f(x) называется прямая линия, расстояние от которой до графика стремится к нулю при неограниченном удалении точки графика от начала координат.

План исследования функции и построения графика

1. Найти область определения 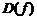функции .

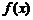2. Найти область значений 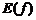(если это возможно вначале, часто 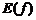можно указать только по результатам исследования).

3. Исследовать функцию на четность.

4. исследовать на периодичность.

5. Найти точки пересечения с осями Ox (нули функции) и Oy.

6. Найти промежутки знакопостоянства функции.

7. Исследовать на непрерывность, дать классификацию разрывов.

8. Найти асимптоты графика функции (горизонтальную, вертикальную, наклонную).

9. Исследовать на монотонность и экстремум.

10. Исследовать на выпуклость, вогнутость, перегиб.

11. Построить график функции.

На множестве X задана структура метрического пространства, если задана функция двух переменных, называемая метрикой, удовлетворяющая следующим аксиомам: r(x; y) = r(y; x); r(x; y) = 0 Û y = x; " x, y, z r(x; z) £ r(x; y) + r(y; z).

Множество D на плоскости назовем открытым, если оно содержит каждую свою точку вместе с некоторой окрестностью.

Назовем точку z Î D предельной, если в каждой ее окрестности есть точки из множества D.

Если множествоD содержит все свои предельные точки, то оно называется замкнутым.

Предел функции нескольких переменных.Число A называется lim (x®x0,y®y0) Û " e > 0 $ d-окрестность точки (x0; y0) " (x; y) Î d- окрестности (x ¹ x0 и y ¹ y0) ïf(x, y) - Aï < e.

Непрерывность функции нескольких переменных. Функция z = f(x, y) называется непрерывной в точке (x0; y0), если она определена в окрестности этой точки и lim (x®x0, y®y0) f(x, y) = f(x0, y0) (по любому пути).

Частные производные.Назовем частным приращением по xследующее выражение Dxf = f(x + Dx, y) – f(x, y) и частным приращением по y следующее выражение Dyf = f(x, y + Dy) – f(x, y).

Частной производной по xназывается lim (Dx®0) Dxf/Dx = ¶f/¶x (x, y) = f’x.

Частной производной по yназывается lim (Dy®0) Dyf/Dy = ¶f/¶y (x, y) = f’y.

Если дифференцируемая функция принимает выражение Df = f’yDy +f’xDx + a(x, y) + b(x, y), где a/ÖDx²+Dy² ® 0 и b/ÖDx²+Dy² ® 0, то выражение f’xdx + f’ydy называется полным дифференциалом функции f и обозначается df.

Касательная плоскость.Касательная плоскость, проходящая через точку M0 некоторой поверхности имеет следующее свойство: угол между этой плоскостью и любой секущей MM0 (M Î плоскости) ® 0, при M ® M0.

Уравнение нормали в каноническом виде: (x –x0)/ (¶f/¶x) = (y – y0)/ (¶f/¶y) = (z – z0)/ (¶f/¶z)

Функцияz = f(x, y) имеет локальный максимумв точке (x0, y0), если в окрестности этой точки значение f’(x – x0) > f(x, y) " (x, y).