Как составить уравнение прямой с угловым коэффициентом?

Если известна точка 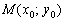, принадлежащая некоторой прямой, и угловой коэффициент 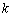этой прямой, то уравнение данной прямой выражается формулой:

Общее уравнение прямой имеет вид: 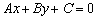, где – некоторые числа. При этом коэффициенты одновременно не равны нулю, так как уравнение теряет смысл.

Как найти направляющий вектор по общему уравнению прямой?

Очень просто:

Если прямая задана общим уравнением 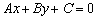в прямоугольной системе координат, то вектор является направляющим вектором данной прямой.

Примеры нахождения направляющих векторов прямых:

Если прямая задана общим уравнением 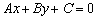в прямоугольной системе координат, то вектор является вектором нормали данной прямой.

Как составить уравнение прямой по точке и вектору нормали?

Если известна некоторая точка 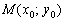, принадлежащая прямой, и вектор нормали этой прямой, то уравнение данной прямой выражается формулой:

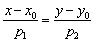
Билет 13.Плоскость в пространстве.

Билет 14. Эллипс. Эллипс – это множество всех точек плоскости, сумма расстояний до каждой из которых от двух данных точек , называемыхфокусамиэллипса, – есть величина постоянная, численно равная длине большой оси этого эллипса: .Каноническое уравнение эллипса имеет вид

, где – положительные действительные числа, причём . Если эллипс задан каноническим уравнением , то его фокусы имеют координаты , где – это расстояние от каждого из фокусов до центра симметрии эллипса.

Эксцентриситетом эллипса называют отношение , которое может принимать значения в пределах .

Вопрос 15 Гипербола. Каноническое уравнение гиперболы имеет вид

, где – положительные действительные числа. У гиперболы две симметричные ветви.

У гиперболы две асимптоты.

Вопрос 16, Парабола

Параболой называется множество всех точек плоскости, равноудалённых от данной точки и данной прямой , не проходящей через точку .

Точка называется фокусом параболы, прямая – директрисой (пишется с одной «эс») параболы. Константа «пэ» канонического уравнения называется фокальным параметром, который равен расстоянию от фокуса до директрисы. . При этом фокус имеет координаты , а директриса задаётся уравнением .

Вопрос 17.Числовая последовательность и ее предел. Числовой последовательностью называется бесконечное множество чисел

(1)

следующих одно за другим в определенном порядке и построенных по определенному закону, с помощью которого задается как функция целочисленного аргумента, т.е. .

Число А называется пределом последовательности (1), если для любого существует число , такое, что при выполняется неравенство . Если число А есть предел последовательности (1), то пишут

Числовая последовательность не может иметь более одного предела. Последовательность, имеющая предел, называется сходящейся.

Для сходящихся последовательностей имеют место теоремы:

если .

Вопрос 1 8.Предел функции в точке. Число А называется пределом функции в точке х_о (или при х→х_о), если для любого положительного ε найдется такое положительное число δ, что для все х¹х_о, удовлетворяющих неравенству |х-х_о|<δ, выполняется неравенство |ƒ(х)-А|<ε.

Вопрос 19.Свойства пределов..

.

Теорема 6. предел произведения равен произведению пределов.

.

Следствие. Постоянный множитель можно выносить за знак предела.

.

Теорема 7. Если функции f(x) и g(x) имеют предел при ,

причем , то и их частное имеет предел при , причем предел частного равен частному пределов.

, .

Вопрос 20.Неопределенности в пределах.

Неопределенности - выраженийя значение которых не определено. основные виды неопределенностей: ноль делить на ноль (0 на 0), бесконечность делить на бесконечность , ноль умножить на бесконечность , бесконечность минус бесконечность , единица в степени бесконечность , ноль в степени ноль , бесконечность в степени ноль .

Вопрос 21. Бесконечно большая величина. Не существует такого понятия как «просто бесконечно малая функция» или «просто бесконечно большая функция». Функция может быть бесконечно малой или бесконечно большой только в конкретной точке. Начертим линию :

Данная функция бесконечно малА в единственной точке:
В точках «плюс бесконечность» и «минус бесконечность» эта же функция будет уже бесконечно большой: . Или в более компактной записи: