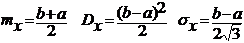Характеристики положения случайной величины.
Модой (Мо)случайной величины х называется наиболее вероятное ее значение. Это определение строго относится к дискретным случайным величинам.
Для непрерывной величины модой называется такое ее значение для которого ф-ция плотности распределения имеет максимальную величину.
Медианой (Ме)случайной величины называется такое ее значение для которого окажется ли случайная величина меньше этого значения.
Для непрерывной случайной величины медиана это абсцисса точки в которой площадь под кривой распределяется пополам.
Для дискретной случайной величины значение медианы зависит от того четное или нечетное значение случайной величины
n=2k+1, то Ме=хк+1 (среднее по порядку значение)
Если значение случайных величин четное, т.е n=2k, то 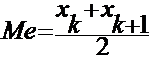
Математическое ожидание случайной величины.
Математическим ожиданием случайной величины х (M[x])называется средне взвешенно значение случайной величины причем в качестве весов выступают вероятности появления тех или иных значений.
Для дискретной случайной величины
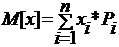
Для непрерывной
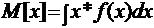
С механической точки зрения мат. Ожидание это абсцисса центра тяжести системы точек расположенных по одноименной оси. Размерность мат. Ожидания совпадает с размерностью самой случайной величины.
Математическое ожидание случайной величины всегда больше наименьшего значения и меньше наибольшего.
Характеристики рассеяния.
Дисперсия
Дисперсия (D[x]) характеризует рассеивание или разряженность случайной величины около ее математического ожидания.
Для дискретных 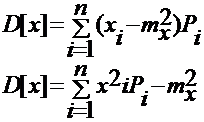
Для непрерывных
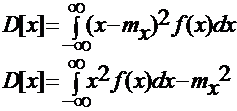
Дисперсия случайной величины всегда величина положительная
Размерность дисперсии равна квадрату разности случайной величины
Среднеквадратическое (стандартное) отклонение.
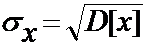
Некоторые законы распределения случайных величин.
Для дискретных случайных величин - биномиальное распределение и распределение Пуассона
Для непрерывных - равномерное показательное, экспоненциальное и нормальное распределение.
Биномиальное распределение.
Биномиальным называют законы распределения случайной величины Х числа появления некоторого события в n опытах если вероятность р появления события в каждом опыте постоянна
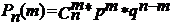
Сумма вероятностей представляют собой бином Ньютона
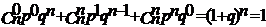
Для определения числовых характеристик в биномиальное распределение подставить вероятность которая определяется по формуле Бернули.
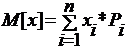
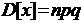
При биномиальном распределении дисперсия равна мат. Ожиданию умноженному на вероятность появления события в отдельном опыте.
Распределение Пуассона
Когда требуется спрогнозировать ожидаемую очередь и разумно сбалансировать число и производительность точек обслуживания и время ожидания в очереди. Пуассоновским называют закон распределения дискретной случайной величины Х числа появления некоторого события в n-независимых опытах если вероятность того, что событие появится ровно m раз определяется по формуле.
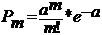 a=np
a=np
n-число проведенных опытов
р-вероятность появления события в каждом опыте
В теории массового обслуживания параметр пуассоновского распределения определяется по формуле
а=λt , где λ - интенсивность потока сообщений t-время
Необходимо отметить, что пуассоновское распределение является предельным случаем биномиального, когда испытаний стремится к бесконечности, а вероятность появления события в каждом опыте стремится к 0.
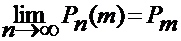
Пуассоновское распределение является единичным распределением для которого такие характеристики как мат. Ожидание и дисперсия совпадают и они равны параметру этого закона распределения а.
Закон равномерной плотности
Равномерным называется распределение непрерывной случайной величины Х все значения которой лежат на отрезке [a;b] и имеют при этом постоянную плотность распределения
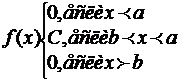
площадь под кривой распределения равна 1 и поэтому с(в-а)=1
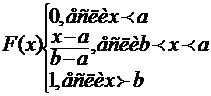
вероятность попадания случайной величины Х на интервал от (α;β)
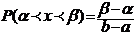
α=а, если α<а
β=в, если β>в
основные числовые характеристики закона распределения плотности вычисляются по общим формулам и они равны