Скалярное и векторное умножение тензора на вектор и тензор. Единичный тензор.

Скалярное произведение – самая распространенная операция. Пусть

.

По определению, умножение справа: ) = ,

умножение слева: =

В обоих случаях вектор скалярно умножается на ближайший в каждой диаде вектор, и в результате получается новый вектор; отсюда, по-видимому, следует принятое в математике определение тензора как « линейного оператора, преобразующего векторное пространство само в себя». Впрочем, и это крайне узкое определение имеет смысл. Пусть тензор – одна диада 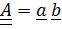. Тогда при умножении его, например, справа на любой вектор получается – вектор, коллинеарный вектору - отсюда и его название «линейный тензор». Если – сумма двух диад, то при умножении его (например) справа на любой вектор получится вектор , лежащий в плоскости векторов и – отсюда и название «плоский тензор»: все векторы «ложатся» на одну плоскость.

Аналогично умножению на вектор вводится скалярное умножение тензора на тензор. Пусть 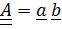, . Тогда

( ) - новый тензор.

Правило осталось тем же: скалярно перемножаются ближайшие векторы в диадах.

1.Показать, что и, следовательно, для симметричного тензора а для кососимметричного ( )

2. Показать, что

Пусть тензоры записаны в координатном виде , .

Тогда

, откуда из получаем правило перемножения матриц , которое в линейной алгебре вводится «по определению».

Единичным тензором называется тензор, в результате скалярного произведения на который слева или справа вектора ( или тензора) получается тот же самый вектор (или тензор.)

Разложение вектора по базису имеет вид = ( , где, согласно определению, - единичный тензор.

Обратным к тензору. называется тензор ,являющийся решением уравнения . 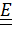или, что равносильно, .

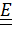Векторное умножение тензора на вектор достаточно показать на одной диаде

- получается новый тензор.

Упражнение. Доказать тождество (1.7)

и, умножив его скалярно на , получить формулу (1.6) двойного векторного произведения.

4.След, векторный инвариант, определитель тензора. Теорема о представлении кососимметричного тензора.

След (trace) тензора - число, получаемое заменой диадного умножения на скалярное:

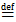
. (1.8)

Если тензор записан в координатном виде ,

то - сумма элементов главной диагонали матрицы. В силу своего определения при любой замене базиса след тензора не изменяется (скалярные произведения от базиса не зависят), поэтому его называют первым инвариантом тензора.

Векторным инвариантом тензора называется вектор, полученный заменой диадного произведения векторным:

или (1.9)

Векторный инвариант симметричного тензора, у которого равен нулю; . что же касается кососимметричного тензора, то можно доказать теорему:

Теорема. Произвольный кососимметричный тензор 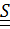может быть единственным образом представлен в виде , (1.10)

где называется сопутствующим вектором тензора .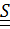

Доказательство. Поскольку , то и 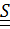можем записать в виде

Найдем вектор и обозначим его : .

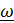Поскольку координаты 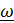содержат по одной лишь компоненте тензора 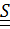, а не их комбинации, то сопутствующий вектор определяется через 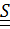единственным образом. Обратно, умножив , убедимся, что .

Определителем (детерминантом) тензора называется число:

, (1.11)

Очевидно, что определение (1.11) не зависит от системы координат и, более того, можно доказать, что оно не зависит и от выбора тройки некомпланарных векторов . Запишем тензор в виде и обозначим для простоты .Тогда

и с помощью (1.5) выражение (1.11) принимает вид определителя матрицы координат тензора в ортонормированном базисе:

(1.12)

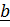Определитель тензора имеет простой геометрический смысл. Обозначим , , . Тогда, вспомнив, что смешанное произведение – объем построенного на перемножаемых векторах параллелепипеда, получим: -отношение «деформированного и повернутого» объема к исходному.