Евклидово и унитарное пространства.

Ортогональные и ортонормированные базисы. Умножения векторов: скалярное, векторное, смешанное. Преобразование базисов. Норма вектора

Аксиоматика евклидова и унитарного пространства.

Вещественным евклидовым пространством называется линейное пространство на множестве вещественных чисел и задано отображение пары элементов в вещественное число, т.е. и задано отображение, которое называется скалярным отображением, удовлетворяющим следующим условиям: 1). ; 2). ; 3). ; 4). .

Унитарным евклидовым пространством называется линейное пространство, определенное над множеством комплексных чисел. На этом пространстве определено отображение пары элементов на комплексное число, которое называется скалярным отображением и удовлетворяет условиям: 1).антикоммутативность ; 2).дистрибутивность ; 3). ; 4). .

Свойства унитарного пространства, отличающие от вещественного евклидового пространства: 1). ; 2). ; 3). ; 4).в ортонорм.базисе ; 5). .

В унитарном пространстве применим метод ортоганизацииГраммыШмидта, но при этом надо помнить, что сомножители в скалярном произведении менять нельзя.

Ортогональность.

Векторы , вещественного евклидового пространства ортогональны, если их скалярное произведение равно 0.

Пусть задано векторное евклидово или унитарное пространство. Пусть - подпространство заданного пространства. Вектор ортогонален подпространству , если он ортогонален каждому вектору этого подпространства.

ТЕОРЕМА: Вектор ортогонален подпространству тогда и только тогда, когда ортогонален базисным векторам, принадлежащим

Неравенство Коши-Буняковского.

ТЕОРЕМА: Для произвольных элементов выполняется неравенство: ДОКАЗАТЕЛЬСТВО: Рассмотрим …. , т.к.заданное неравенство выполняется при всех значениях , то в качестве можно принять . Тогда подставим в полученное выражение, Получим ч.т.д.

Ортонормированные базисы, их построение.

Базис – упорядоченная система из n векторов, удовлетворяющая условиям: 1). Система линейно независимая; 2).Система максимальна.

Базис называется ортогональным, если все векторы базиса попарно перпендикулярны.

Базис называется ортонормированным, если он ортоганальный и все базисные векторы имеют длину равную 1.

В евклидовом пространстве ортонормированным базисом называется линейно независимая система векторов, которые попарно ортогональны и длины векторов равны 1.

ТЕОРЕМА: в евклидовом пространстве любую линейно независимую систему можно ортонормировать и привести к ортонормированному базису (метод органализации Граммы Шмидта).

Скалярное произведение в ортонормированных базисах.

Скалярным произведением векторов и называется число, которое обозначается .

Физический смысл: Пусть задана материальная точка , на которую действует сила и перемещает эту точку на вектор , тогда работа, совершенная силой по перемещению точки на вектор , будет равна их скалярному произведению . Т.е. .

В ортонормированном базисе ( ) заданы вектора и , тогда

Доказательство: на основании свойства (если , значит ) . Из определения скалярного произведения: . Учитывая, что , . Получаем .

ТЕОРЕМА: Скалярное произведение двух векторов евклидового пространства равно .

Преобразование ортонормированных базисов.

Рассмотрим старый базис и новый базис . Тогда переход из старого базиса в новый , C – матрица перехода (преобразования базисов).

Выразим координаты вектора в старом базисе через координаты вектора в новом базисе. , - матрица перехода.

Т.О.: ;

Структура матрицы перехода.

Норма векторов.

Нормой вектора евклидова пространства называется арифметический квадратный корень из скалярного квадрата вектора. Обозначается ||a||.

Теорема: Если a, b – векторы евклидова пространства и λϵR, то: 1).||a||≥0, причем ||a||=0 тогда и только тогда, когда a=0; 2). ||λ·a||=|λ|·||a||; 3). |a·b|≤||a||·||b|| (неравенство Коши-Буняковского); 4). |a+b|≤||a||+||b|| (неравенство треугольника);

Векторное трехмерное пространство направленных отрезков.

Векторным пространством называется множество векторов, каждый из которых может быть представлен линейной комбинацией в базисе , который называется базисом этого пространства. И для всех векторов выполняются операции сложения и умножения на число и все их свойства.

Число 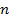векторов базиса называется размерностью векторного пространства .

Векторное произведение его свойства и вычисление в ортонормированном базисе.

Векторным произведением векторов и называется вектор, который обозначается .

Ориентация тройки векторов ( ) имеет правую ориентацию, если 1).либо обход этих векторов осуществляется против часовой стрелки; 2).либо, если смотреть из конца вектора , то обход от вектора к вектору осуществляется против часовой стрелки; 3).либо ( ) совмещаются соответственно с большим, указательным, средним пальцем правой руки.

Ориентация тройки векторов ( ) имеет левую ориентацию, если 1).либо обход этих векторов осуществляется по часовой стрелке; 2).либо, если смотреть из конца вектора , то обход от вектора к вектору осуществляется по часовой стрелке; 3).либо ( ) совмещаются соответственно с большим, указательным, средним пальцем левой руки.

Векторным произведением векторов и называется вектор, удовлетворяющий следующим условиям: 1). ; 2). ; 3). - правая ориентация, или ориентация, совпадающая с базисной ориентацией ( ).

Свойства: 1).Геометрический смысл: длина модуля векторного произведения равна площади параллелограмма, построенного на этих векторах, как на сторонах; 2).Векторное произведение антикоммутативно ; 3). , ; 4).Дистрибутивность ; 5). , Следствие: ; 6).Пусть задан ортонормированный базис ( ) и и ,тогда ,,

Смешанное произведение его свойства и вычисление в ортонормированном базисе.

Смешанным произведением векторов является .

Свойства: 1).Геометрический смысл: смешанное произведение трех векторов равно объему параллелепипеда, построенному на этих векторах; 2) ; 3). - комплонарны, - правая ориентация, - левая ориентация; 4). меняет знак при перестановке любых двух вектор, , , ; 5).При циклической перестановке векторов знак не меняется; 6).Пусть в базисе ( ) векторы заданы своими координатами, тогда смешанное произведение ; 7). ; 8).( )= .