Статистическая фильтрация Байеса
Суть метода статистической фильтрации состоит в разбиении входящих писем на условные слова (токены), составлении частотного словаря таких токенов и применении математической теоремы Байеса к полученным наборам слов. Эта теорема позволяет вычислить вероятность успешного совершения некоторого события на основании статистики совершения этого события в прошлом. Применительно к фильтрации спама: если 9 из 10 писем, содержащих пресловутое слово "корова", являются спамом, и лишь одно — "хорошим" письмом, то теорема Байеса позволяет вычислить, с какой вероятностью следующее письмо, содержащее это слово, будет являться спамом.
Метод Байеса подразумевает использование статистической оценочной базы — двух наборов ("корпусов") писем, один из которых составлен из спама, а другой — из "хороших" писем. При создании этой базы подсчитывается количество вхождений каждого отдельного слова (токена) в каждом корпусе, и на основании этого для каждого токена вычисляется оценка, или "спамность".
"Спамность" измеряется по шкале 0..1. Значение "0" означает отсутствие спама, "1" — полную уверенность в том, что это спам. Нейтральное значение — 0,5 — выражает отсутствие какой-либо определённой оценки. Токены, чья "спамность" приближается к нейтральному значению, малоинтересны для оценки письма. Наоборот, те из них, чьи значения очень сильно отличаются от 0,5, являются яркими показателями письма.
Пусть письмо содержит n токенов с оценками S1...Sn.
Тогда общая оценка письма S может быть легко вычислена по следующей формуле:
a = S1*S2*...*Sn;
b = (1-S1)*(1-S2)*...*(1-Sn);
S =a/(a+b).
Полученная оценка и будет являться значением "спамности" для некоего письма на основании существующей статистической оценочной базы.
Пауль Грэхем и Гари Робинсон
Допустим, что в оценочной базе некий токен "корова" встретился в 200 письмах спама и 100 - не-спама, а токен "бык" - в 1 письме спама и 0 не-спама. Легко сказать, что "спамность" первого токена в 2 раза превышает его не-спамность (и составляет 2/3), но как быть во втором случае? Можно сказать, что "бык" означает абсолютную спамность, но ведь он же встретился лишь единожды! Может, он вообще случайно оказался в базе...
Существует, по крайней мере, два подхода к этой проблеме. Один из них выражен в статье Пауля Грэхема "План по спаму". Второй — в статье Гари Робинсона, аналогичного содержания. Согласно первому подходу, все токены, общая частота которых меньше определённой величины (пусть, для определённости, будет 5), просто игнорируются. Согласно второму, их спамность вычисляется по формуле, которая при нулевой частоте даёт нейтральный результат (0,5 или 0,4), а при увеличении частоты асимптотически приближается к реальной оценке.
Другая проблема касается токенов, впервые встретившихся в проверяемом письме и не существовавших до этого в базе. Подход Робинсона, как было только что упомянуто, легко справляется с этой проблемой. Пауль Грэхем же предлагает для таких токенов дать оценку 0,4, из соображения, что спамеры редко придумывают новые слова, и если где-то встретилось абсолютно новое слово, то пусть оно воспринимается с лёгким сдвигом в сторону не-спамности.
Эвристический интервал
Когда вы визуально оцениваете письмо, вам необязательно читать его целиком. Обычно вы догадываетесь о том, что это спам, по нескольким ключевым признакам, срабатывающим на уровне подсознания. Точно так же, для статистической фильтрации вовсе необязательно вычислять оценку письма по всем его токенам. Достаточно выбрать лишь некоторые из них, наиболее "интересные" с точки зрения оценок. Уровень "интересности" определяется тем, насколько оценка токена отличается от нейтральной.
Эвристическим параметром для статистической фильтрации писем будет количество токенов, по которым оценивается то или иное письмо. Пауль Грэхем предлагает в качестве такого параметра число 15.
Наличие эвристического параметра позволяет существенно улучшить эффективность оценки и практически довести эффективность фильтра до 99,7%
Трюки спамеров...
В последнее время спам тоже не стоит на месте. Появились новые технологии, позволяющие спамерам с лёгкостью обманывать многие автоматические фильтры. Например, писать текст, невидимый для пользователя, но, естественно, "видимый" фильтрам и убеждающий их в том, что, мол, всё здесь в порядке. В последнее время для спамеров стало очень популярным оформлять свою рекламу в виде сравнительно небольшой картинки - в формате gif или jpeg - и посылать её как вложение. Однако с таким трюком легко справляется фильтр, который распознаёт файл-картинку не просто как вложение, но именно как картинку, причём определённого размера. Иногда это работает, но на практике обычно фактическая фильтрация производится по другим признакам - незначительным деталям заголовков писем, известным только фильтру благодаря набранной статистике.
Другой, становящийся популярным вариант - отправка текстовых писем, в которых ключевые слова разрежены при помощи пробелов. Но и это не срабатывает: поскольку нормальные письма обычно не содержат отдельно стоящих букв (не считая коротких предлогов и союзов), то уже после нескольких подобных спамерских проделок такие буквы начинают действовать на фильтр, как красная тряпка на быка...
Можно опробывать таким образом множество возможных трюков спамеров. Однако практика показывает, что при достаточно большой собранной базе фильтр даже без распознавания спец. трюков на клиентской легко справляется практически с любым (даже самым новым) спамом, отфильтровывая 99.4%..99.9% всего спама, попадающего в ящик.
Повторение опыта
В электроэнергетике часто возникают задачи, в которых сложность опыта состоит в том, что элементарный опыт, вследствие которого может появиться или не появиться событие А проводится много раз. Нас интересует вероятность разных результатов этого опыта.
Рассмотрим независимые опыты в одинаковых условиях появления события А (р(А)).
Обозначим
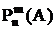 - вероятность того, что при n независимых испытаний событие А произойдет m раз.
- вероятность того, что при n независимых испытаний событие А произойдет m раз.
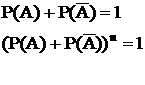
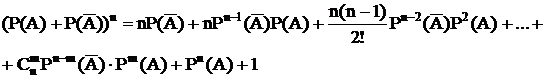
| |
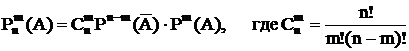
Формула биноминального распределения.
Первый сомножитель – вероятность того, что событие ‘А’ не произойдет ни разу. Второй сомножитель – вероятность того, что событие А произойдет один раз. и т.д.
Очень часто возникает задача
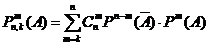
В практике энергетических расчетов часто появляется необходимость определения вероятности того, что разные группы однотипных событий возникают одновременно при разной их повторяемости.
Рассматривая эти события как независимые и совместные на основе теории умножения:
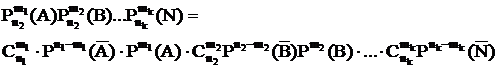
Пример:
В энергосистеме работают 5 однотипных агрегатов. Рассмотрим их повреждения как случайные равновероятные события определенной вероятности. Определить вероятность 1) одновременного повреждения всех n из 5-ти агрегатов и 2) 3-х из n агрегатов. Если вероятность повреждения 1-го агрегата: Р(А)=2×10-2
Решение:
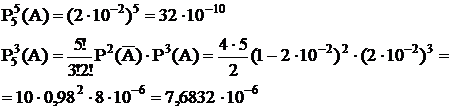
Пример:
В системе работают 3 группы агрегатов. В границах каждой группы агрегаты можно рассматривать как однотипные со следующими вероятностнім повреждением отдельных агрегатов.
р*(А)=0,05
р*(В)=0,08
р*(С)=0,04
n1=5
n2=3
n3=6
Определить вероятность одновременного повреждения одного агрегата 1-й группы, 2-х агрегатов 2-й группы и 3-х агрегатов 3-й группы.
(m1=1, m2=2, m3=3)
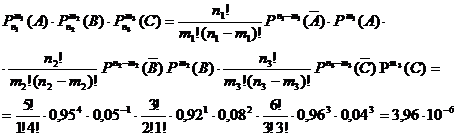
Случайные величины
Случайной величиной называется величина, которая принимает разные значения при повторении опытов.
Случайные величины – температура воздуха, атмосферное давление.
Случайные величины делятся на:
1. Дискретные
2. Непрерывные.
В 1-м случае она может приобретать отдельные, заранее неизвестные значения (число отказов, число успешной работы АВР);
во 2-м – принимает любые значения в некотором интервале (время безотказной работы, значения тока линии и т.д.)
Для дискретных случайных величин распределение вероятности различных их значений может быть наиболее просто задано с помощью таблиц распределения, в которых в верхней строке указаны все значения, которые может принять случайная величина, в нижней – их вероятность.
Сумма вероятностей равна 1, если случайные величины всегда принимают одно из этих возможных значений:
| число агрегатов | … | n | |||
| вероятность Рm | 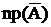 | 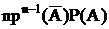 | 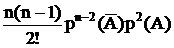 | 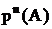 |
Законом распределения случайных величин называется всякое соотношение, которое установило связь между возможным значением случайной величины и их вероятностью.
Таблица называется рядом распределения случайных величин.
Функция распределения F(x) является исчерпывающей характеристикой любой случайной величины и определяет вероятность того, что случайная величина х окажется меньше некоторого значения х (маленькое).
Функция распределения дискретных случайных величин изменяется от 0 до 1 скачками в точках возможных значений случайной величины.
При непрерывных случайных величинах имеем непрерывно возрастающую функцию.
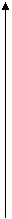
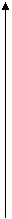 F(x)
F(x)

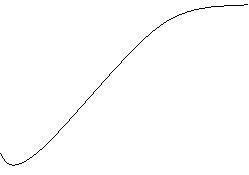



 1 1
1 1
 |



 0,5
0,5







 0
0
х1 х2 х3 х4 х 0 x
для дискретной случайной для непрерывной случайной
величины величины
Для дискретной случайной величины:
F(-¥)=0 F(+¥)=1
P(x1 £ x £ x2) = F(x2) – F(x1)
Функция распределения является наиболее универсальным законом распределения, характеризующим связь между случайной величиной и вероятностью ее появления.
Закон распределения может быть задан аналитически в виде таблицы или графически.
Аналитически: F(x) = …
таблица:
| xi | x1 | x2 | … | xn |
| P1 | P |
Графически функция задается в виде многоугольника распределения.
 Р (хi, Pi)
Р (хi, Pi)


 1 -
1 -
 | |||
 |
x1 x2 x3 x4 x
Для непрерывных случайных величин.
Наиболее полной характеристикой непрерывных случайных величин является плотность распределения f(x)
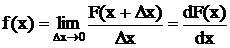
lim отношения вероятности попадания случайной величины в какой-то промежуток и этому промежутку при бесконечном сближении границ этого промежутка
| |
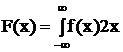
F(x) – функция распределения.
Если f(x) задана аналитически, то вероятность попадания случайной величины в промежуток от х1 до х2 равна:
| |
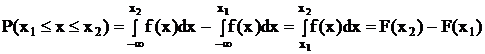
 f(x)
f(x)
 x1 x2 x
x1 x2 x
