Алгебра высказываний и логика предикатов.
Логические связки алгебры высказываний:
НЕ - 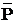 ИЛИ - Р
ИЛИ - Р  q
q
И - 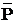 &
& 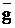 ЕСЛИ…, то - Р ® q (импликант)
ЕСЛИ…, то - Р ® q (импликант)
Семантическая область алгебры высказываний содержит всего 2 значения:
истина и ложь( 1 и 0 ). Каждое элементарное высказывание обозначается малыми латинскими буквами (литералы). Используя элементарные высказывания и логические связки, можно составить сложные высказывания. Алгебра высказываний базируется на алгебре Буля, а в алгебре Буля аналогично высказываниям – функция.
Если некоторое высказывание в качестве аргументов имеет m литералов, то оно m – местное.
Буквой Е в высказываниях обозначается множество всех высказываний от m – аргументов. Все множество высказываний можно разделить на 3 класса:
1. Общезначимые высказывания (тарфтология)
2. Выполнимые высказывания.
3. Невыполнимые высказывания.
Общезначимое - высказывание , принимающее значение ИСТИНА для любых наборов литералов.
Выполнимые – высказывания, которые имеют хотя бы одну интерпретацию.
Интерпретационные высказывания – некоторый набор литералов, при котором высказывание принимает значение ИСТИНА.
Высказывание, которое не имеет на одной интерпритации, называется невыполнимым.
Основными задачами алгебры высказываний являются алгоритмы определения выполнимости и общезначимости высказываний. Так как АВ базируется на Булевой алгебре, то все методы последней применимы к первой , в том числе и методы представления функций.
Основная форма представления высказываний является ДСНФ , а иногда и КСНФ.
| p | q | v | y |
ДСНФ
 f ( p, q, v ) =
f ( p, q, v ) = 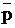
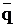 v
v 
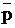 q
q 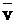
 p
p 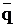
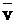
 pq
pq 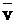
КСНФ
f ( p, q, v ) = ( p  q
q  v ) & ( p
v ) & ( p 
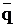

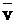 )
)  (
( 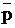
 q
q 
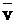 ) & (
) & ( 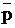

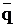

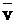 )
)
ДСНФ и КСНФ можно свести к ДНФ и КНФ.
 Сведем КСНФ к КНФ.
Сведем КСНФ к КНФ.
p q v 00 01 11 10
| 0 | ||||
| 1 |
КНФ
f ( p, q, v ) = ( p  q
q  v ) & (
v ) & ( 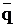

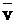 ) & (
) & ( 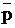

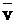 )
)
Анализ высказываний, представленных в ДНФ.
Задача в ДНФ общезначна, если каждый из ее элементов общезначен (дизъюнкт). Высказывание выполнимое в ДНФ , если выполним хотя бы один дизъюнкт.
Пример.
Дано сложное высказывание, зависящее от 3-х литералов p, q, r, заданное таблично:
| p | q | r | A1 | A2 |
 Представим высказывания А1 и А2 в ДНФ, для этого составим карты Карно :
Представим высказывания А1 и А2 в ДНФ, для этого составим карты Карно :
А1 p q r 00 01 11 10
| 0 | ||||
| 1 |
 A1 = qr +
A1 = qr + 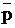
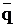 + p
+ p 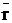
А2 p q r 00 01 11 10
| 0 | ||||
| 1 |
A1 = q + pr
Тогда высказывание f имеет вид:
f = qr + 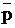
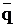 + p
+ p 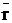 + q + pr
+ q + pr
По полученному f можно сделать вывод, что высказывание является выполнимым. Это следует из того ,что выполнимым является 1 из дизъюнктов, например pr , если p = 1 и r = 1 , то pr = 1 и следовательно все высказывания принимают значение true.
Логика высказываний занимаетсяся логическими связями, а логика предикатов проникает в структуру высказываний и исследует связь того, о ком или о чем идет речь (субъект) с тем, что говорится о данном объекте (предикат). Поэтому язык логики предикатов лучше приспособлен для выражения логических связей между различными понятиями и утверждениями P(x1, x2, …,xn).
N – местный предикат есть неоднородная двузначная логическая функция
Аргументы х1,х2,хn представляют собой объекты из множеств их представления, т.е. х1 Î х1
х2 Î х2
Конкретное значение аргументов называют предметными постоянными. Предметные переменные и const образуют класс логических понятий – термы. При замещении аргумента Хк (предмет var), некоторым его значениям а (предмет const) n – местный предикат р(х1,х2, …,хn) превращается в ( n – 1 ) местный предикат p(x1,x2,…ki-1,a,ki+1,xn). И от переменной хn он уже не зависит. Присвоив значение всем переменным n местного предиката из соответствующих областей определения, мы получим высказывание,которое можно рассматривать как О местный предикат.
Например: дан 3-х местный предикат p(x1,x2,x3) для которых х1 есть сумма х2 и х3
При подстановке х1 = 5 он переходит в двуместный предикат вида
р (5,х2,х3)
При подстановке х2 = 2 он переходит в одноместный предикат вида
р (5,2,х3)
При х3 = 3 , он становится истинным высказыванием
При х3 ¹ 3 - ложным.
В логике предикатов большое значение имеют две операции, которые называются КВАНТОРН., с помощью которых выражается отношение общности к существованию.
Пусть предикат р(х) определенный на множестве М , утверждение , что все х Î М и обладают свойством р(х) , записывают с помощью квантора общности
" x p(x) {Для всех х ,р(х) }.
Утверждение ,что существует хотя бы 1 объект х из множества М , обладающий свойством р(х), записывается с помощью квантора существования:
$ х р(х) {существует такой х, что р(х)}
В этих двух выражениях встречаются переменные х , но они не зависят от значения этой переменной. Кванторы общности и существования связывают переменные х , превращая одноместный предикат в высказывание.
Рассмотрим предикат р(х) , где х – простое число. Предикат р определен на множестве натуральных чисел. Подставляя вместо х числа натурального ряда, получаем счетное множество высказываний. Некоторые из них р(1),р(2),р(3)…. являются истинными. Высказывание " х р(х) – ложное, а $ х р(х) для 2-го предиката (некоторые числа простые) – истинными.Между кванторами общности и существования имеют место соотношениния, обобщающие законы де Моргана вида:
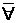 х р(х) = $ х
х р(х) = $ х 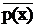
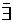 х р(х) = " х
х р(х) = " х 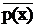
Применение квантора к n – местному предикату, превращает его в (n – 1) местный предикат. Кванторы можно также применять к нескольким различным переменным ( по 1 квантору к-л. типа к каждой переменной). Если к n местному предикату применяется k кванторов, то он превращается в
(n – k) предикат.
Переменные , к которым применяются кванторы – связанные , остальные переменные – свободные.
Например: из двуместного предиката р(х,у) можно получить следующий одноместные предикаты:
" x p(x,y)
$ x p(x,y)
" y p(x,y)
$ y p(x,y)
а так же высказывания:
" x " y p(x,y);
" x $ y p(x,y);
…………………
$ x $ y p(x,y); и т.д.
Порядок следования одноименных кванторов не имеет значения, но разноименные переставлять нельзя.
" x " y p(x,y) Þ " y " x p(x,y)
 " x $ y p(x,y) Þ $ y " x p(x,y)
" x $ y p(x,y) Þ $ y " x p(x,y)
В этом можно убедиться на примере:
p(х,у) = << x делит у >>
" x $ y << x делит у >> - это высказывание истинное
$ y " x << y делит x >> - это высказывание ложное.
Категорические высказывания.
В традиционной логике большое внимание уделяется 4-м типам категорических высказываний , которые обозначаются: A, E, I, O.
А – общеутвержденное высказывание.
<< Всякое S суть P >>
Для всех х ,если х обладает свойством S , то х обладает и свойством р.
" x ( S(x) ® p(x))
Е – общеотрицательное высказывание
<< никакое S не есть p >>
" x ( S(x) ® 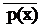 )
)
Для всех х , если х обладает свойством S ,то он обладает свойством р.
I - частноутвердительное высказывание.
<< некоторое S суть р >>
$ x ( S(x) & p(x))
cуществует такой объект х , который обладает свойством S и одновременно обладающий свойством р.
О – частноотрицательное высказывание
<< некоторое S не суть р >>
$ x ( S(x) & 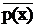 )
)
существует такой объект х, который обладает свойством S и не обладает свойством р.
Пример: S(x) = << x – селедка >>
p(x) = << x – рыба >>
Четырем типам высказываний соответствуют утверждения:
А : всякая селедка – рыба
Е : никакая селедка не является рыбой
I : некоторая селедка – рыба
О : некоторая селедка не является рыбой
В законах де Моргана эти категоричные высказывания выглядят следующим образом:
" x (S(x) ® p(x)) Û 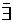 x (S(x) &
x (S(x) & 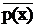 );
);
" x (S(x) ® 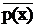 ) Û
) Û 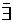 x (S(x) & p(x));
x (S(x) & p(x));
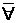 x (S(x) ®
x (S(x) ® 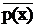 ) Û $ x (S(x) & p(x));
) Û $ x (S(x) & p(x));
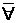 x (S(x) ® p(x)) Û $ x (S(x) &
x (S(x) ® p(x)) Û $ x (S(x) & 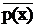 );
);
Высказываеие А и О, а так же Е и I отличаются друг от друга. Если одно из них истинное, то другое – ложно и нызываются противоположными.
ЭЛЕМЕНТЫ ТЕОРИИ АВТОМАТОВ.
Конечный автомат:
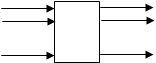 x1 y1
x1 y1
……… КА ………
xn yn
Рассмотрим следующий элемент:
Дано некоторое логическое устройство ,имеющее один вход и один выход:
 |

 х1 у1
х1 у1
На вход подается некоторая двоичная последовательность: х = 011101001101
Алгоритм устройства следующий:
Выходом У будет Å текущего и предыдущего элемента вход. последовательности:
У = 10011101011
С помощью логических устройств, которые мы рассматривали ранее, данная задача не выполнима. Для решения этой задачи нужно применить устройство конечного автомата.
Основные определения:
Декарт. Произведение 2-х множеств АВ называется множество С ,элементы которого составляют пары исходных элементов 2-х множеств.
Пример: С = А*В; А{a1,a2,a3}; B{b1,b2}
C{(a1,b1),(a1,b2),(a2,b1),(a2,b2),(a3,b1),(a3,b2)}
Конечный автомат – объект определенный 5-ю параметрами:
1) S = < A, Q, V, d, l >
A – множество букв входящего алфавита;
Q – множество сост. автомата;
V – множество букв выход. алфавита;
d : A*Q ® Q - функция переход. КА;
l : A*Q ® V - функция выходов
Пример конечного автомата: Задан вход и выход , набор , и набор состояний:
A = {a0,a1}, V = { V0, V1}, Q = { q0, q1, q2}.
Одним из способов задания функции переходов и выходов является табличный метод:
Функция переходов Функция выходов
| d | q0 | q1 | q2 | l | q0 | q1 | q2 | ||
| a0 | q1 | q0 | q2 | a0 | v0 | v1 | v1 | ||
| a1 | q2 | q1 | q0 | a1 | v1 | v1 | v0 |
С помощью 2-х функций из 3-х исходных множеств полностью задается КА.
Кроме табличного способа задания КА можно использовать аппарат графов.
Граф – топологический объект , основными элементами которого являются вершины.

1 2 1,2 – вершины
Ребро графа может соединять вершины и входить само в себя.
1) 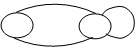 Неориентировочные графы.
Неориентировочные графы.
1 2
Для данного графа имеет значение соединение между собой, направления не учитываются.
2) 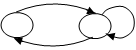 Ориентировочные графы.
Ориентировочные графы.
1 2
Для них важно, какие вершины соединяются и направление соединения.
Словом a называется некоторая последовательность букв входного алфавита.
a = аj1, aj2, …, ajn;
при этом для функции перехода и выходов справедливы соотношения:
d (q, aa) = d ( d (q, a ),a);
l (q, aa ) = l ( d (q, a ),a);
Допустим, что автомат находится в состоянии qi и на его вход поступает последовательность букв: a =aj1, aj2, …, ajn, тогда на выходе автомата будет наблюдаться w следующего вида:
w = l (qi, aj1) l (qi, aj1, aj2) … l (qi, aj1, aj2, aj3, …, ajn)
Другими словами автомат находится в состоянии qi, переводит входное слово
a в выходное w. Другими словами это записывается в виде:
S (qi, a ) = w;
где функция S – автоматный оператор.
