В ы ч и с л е н и я в M a t h c a d’ е
Задание: найти частное решение диф.ур. у´ = f(x,y) с нач. условиями у(x0) = у0
f(x,y) := 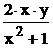 + 1 + x2 x0 := 1 y0 := 1
+ 1 + x2 x0 := 1 y0 := 1
Аналитическое решение:u(x) := x3 – 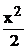 + х –
+ х – 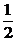
Решение ищем на интервале (x0, xn)
Численное решение:n := 5 xn := 3 h := 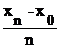
k := 1 .. n xk := xk-1 + h yk := yk-1 + h· f(xk-1, yk-1)
k := 0 .. n zk := u(xk)
Результаты:
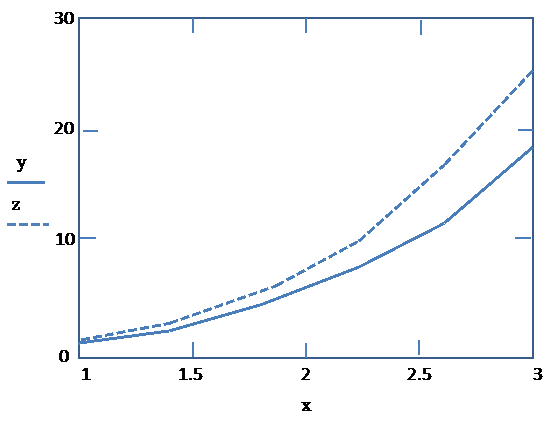
| k= | xk= | yk= | zk= | |||
| 1.4 | 2.2 | 2.664 | ||||
| 1.8 | 4.216 | 5.512 | ||||
| 2.2 | 7.344 | 9.928 | ||||
| 2.6 | 11.894 | 16.296 | ||||
| 18.186 |
Графики численного и аналитического решений
Отлаженную программу необходимо «запомнить» под своим оригинальным именем на своем компьютере и, что очень желательно (во избежание затирания программы другим пользователем), на дискете или на «флэшке».
2.4. Четвертый этап представляет собой защиту работы.
При этом необходимо:
1. Знать теоретические основы численного решения задачи Коши (в пределах данной методички).
2. Уметь объяснять полученные результаты, как-то, как и почему влияет на точность решения число разбиений отрезка интегрирования.
3. Уметь объяснять функциональное назначение отдельных операторов и мест в программе.
4. Показать результаты аналитических расчетов в рабочей тетради.
5. При небольшом значении n (порядка 3 – 5) вручную получить приближенное значение задачи Коши, предложенной преподавателем. При выполнении этого задания можно пользоваться калькулятором или Mathcad’ом.
Пример выполнения такого задания представлен ниже.
Пример выполнения задания ручного счета.
Найти решение дифференциального уравнения 2(y´+ xy) = (x – 1) ex y2 с начальными условиями у (0) = 2 на отрезке [0, 1] с шагом h = 0,25.
Вначале, для того, чтобы проверить результат численного решения, найдем аналитическое решение исходного дифференциального уравнения.
• Перепишем дифференциальное уравнение в виде y´+ xy = 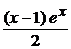 y2. Это уравнение Бернулли вида у¢ + p(x) y = q (x) y2, в котором p(x) = x, q (x) =
y2. Это уравнение Бернулли вида у¢ + p(x) y = q (x) y2, в котором p(x) = x, q (x) = 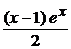 . Общее решение ищем в виде y = uv . Тогда y = u¢v + uv¢ . Имеем:
. Общее решение ищем в виде y = uv . Тогда y = u¢v + uv¢ . Имеем:
u¢v + uv¢ + xuv = 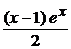 u2v2 => u¢v + u
u2v2 => u¢v + u 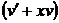 =
= 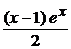 u2v2.
u2v2.
Подберем функцию v так, чтобы v¢ + xv = 0; тогда u¢v = 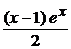 u2v2. Интегрируя первое из этих уравнений, получим:
u2v2. Интегрируя первое из этих уравнений, получим:
v¢ + xv = 0 => 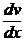 = –xv =>
= –xv => 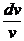 = –xdx => ln |v| = –
= –xdx => ln |v| = – 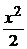 => v =
=> v = 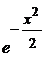 .
.
Подставив полученное выражение для v во второе уравнение, получим:
u¢ 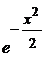 =
= 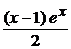 u2
u2 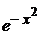 или
или 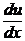 =
= 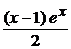 u2
u2 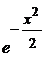 .
.
Имеем:
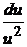 =
= 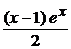
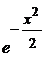 dx или
dx или 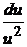 =
= 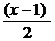
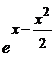 dx.
dx.
Интегрируем: так как 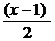
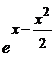 dx = – d
dx = – d  , то
, то
– 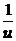 = –
= – 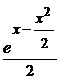 + С, а u =
+ С, а u = 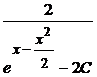 .
.
Общее решение исходного уравнения
y = uv = 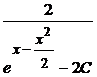 ·
· 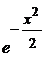 .
.
Подставим в это общее решение начальное условие и получим:
2 = 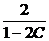 => C = 0.
=> C = 0.
Искомое частное решение имеет вид y = 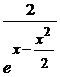 ·
· 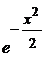 = 2е–х.
= 2е–х.
Для получения численного решения составим таблицу (при составлении таблицы удобно пользоваться Mathcad’ом или Exсel’ем):
| k | xk | Численное решение yk = yk –1+ Δ yk –1 | Δ yk = 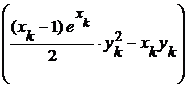 h h | Точное решение |
| –0.5 | ||||
| 0.25 | 1.5 | –0.36 | 1.56 | |
| 0.5 | 1.14 | –0.27 | 1.21 | |
| 0.75 | 0.87 | –0.21 | 0.94 | |
| 0.66 | 0.74 |
Графики численного и точного решений

| |
|
|
|
| |
| |
| |
|
|
|
|
|
|


















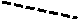

 точное решение
точное решение
численное решение
ЗАДАНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ
Методом Эйлера найти численное решение следующих задач Коши (по выбору преподавателя из каждого варианта выбираются две задачи: одна для составления программы, другая – для ручного расчета):
1. a) y′ – 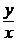 = x2, y(1) = 0; (y = 0,5 x (x2 - 1))
= x2, y(1) = 0; (y = 0,5 x (x2 - 1))
b) y′ + xy = (1 + x) e–x y2, y(0) = 1; (y = ex)
c) Скорость охлаждения тела пропорциональна разности температур тела и окружающей его среды (закон Ньютона). Найти зависимость температуры T от времени t, если тело, нагретое до
T0 = 100о С градусов, внесено в помещение, температура которого постоянна и равна a = 20оС. Через какое время температура тела опустится до 60 оС (принять k = 2 )? (T = a + (T0 – a) e –k t, t = ln 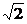 )
)
2. a) y′ = 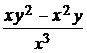 , y(–1) = 1; ( y =
, y(–1) = 1; ( y = 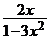 )
)
b) xy′ + y = 2y2 ln x, y(1) = 0,5; ( y = 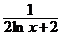 )
)
c) Через сколько времени температура тела, нагретого до 100оС, понизится до 25оС, если температура помещения равна 20оС и за первые 10 мин тело охладилось до 60оС? (Через 40 мин)
3. a) (y2 + xy) d x – x2 dy = 0, y(1) = 1; ( y = 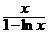 )
)
b) 2(xy′ + y) = xy2, y(1) = 2; ( y = 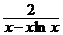 )
)
c) Ж/д состав движется со скоростью 20 км/час. Через одну минуту после выключения двигателя его скорость уменьшилась до 2 км/час. Определить скорость состава через две минуты после остановки двигателя, считая сопротивление движению пропорциональным скорости. (0,2 км/час)
4. a) xy′ – y + x 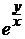 = 0, y(e) = 0; (y = -x lnlnx)
= 0, y(e) = 0; (y = -x lnlnx)
b) y′ + 4 x3 y = 4(x3 + 1) e–4x y2, y(0) = 1; (y = x4)
c) Тело движется по прямой со скоростью, обратно пропорциональной пройденному пути. В начальный момент тело имело скорость v0 = 15 м/с и находилось на расстоянии 4 м от начала отсчета пути. Определить скорость тела через 8 с после начала движения. ( 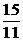 м/с)
м/с)
5. a) y′ – 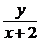 = x2 + 2х, y(–1) =
= x2 + 2х, y(–1) = 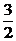 ; ( y = (x + 2) (1 + 0,5x2))
; ( y = (x + 2) (1 + 0,5x2))
b) xy′ = y + x sin 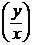 , y(1) =
, y(1) = 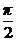 ; ( y = 2x tg(1/x))
; ( y = 2x tg(1/x))
c) Составить дифференциальное уравнение изменения скорости ж/д состава массы m = 10 000 тонн, движущегося со скоростью v0 = 10 м/с, при замедленном прямолинейном движении под действием силы сопротивления, пропорциональной квадрату скорости и равной 20000 Н при скорости 1 м/с. Определить какое расстояние пройдет состав после выключения двигателя, прежде чем его скорость уменьшится до 2 м/с .
(v´= – 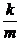 v2; 200 )
v2; 200 )
6. a) y′ – 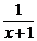 y = ex (x + 1), y(0) = 1; ( y = ex (x + 1))
y = ex (x + 1), y(0) = 1; ( y = ex (x + 1))
b) xy′ = y + 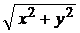 , y(0) = –1; ( y = 0,25 (x2 - 4))
, y(0) = –1; ( y = 0,25 (x2 - 4))
c) Скорость прироста населения страны пропорциональна его численности. Составить дифференциальное уравнение процесса изменения численности населения. Определить численность населения страны через 20 лет, зная что ее население в 2000 году составляло 145 млн человек, а прирост населения за 2000 год был равен –1% .
( 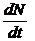 = kN ; N = 145 · (0.99)20 ≈ 119 млн человек )
= kN ; N = 145 · (0.99)20 ≈ 119 млн человек )
7. a) y′ – 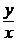 = x sinx, y(π/2) = 1; ( y = 2x/π - xcosx)
= x sinx, y(π/2) = 1; ( y = 2x/π - xcosx)
b) xy′ – y (lny – lnx) = 0, y(–1) = –1; ( y = x ex+1)
c) Скорость прироста населения страны пропорциональна его численности. Составить дифференциальное уравнение процесса изменения численности населения. Определить численность населения страны через 20 лет, зная что ее население в 2000 году составляло 145 млн человек, а прирост населения за 2000 год был равен 2% .
( 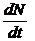 = kN ; N = 145 · (1.02)20 ≈ 215 млн человек )
= kN ; N = 145 · (1.02)20 ≈ 215 млн человек )
8. a) y′ + 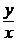 = sinx, y(π) =
= sinx, y(π) = 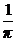 ; ( y = sinx/x – 1/2x – cosx)
; ( y = sinx/x – 1/2x – cosx)
b) y′ = 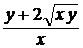 , y(1) = 1; ( y =
, y(1) = 1; ( y = 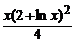 )
)
c) В благоприятных для размножения условиях находится некоторое количество N0 бактерий. Найти зависимость увеличения числа бактерий от времени, если скорость размножения бактерий пропорциональна их количеству. Через сколько времени количество бактерий увеличится втрое? (N = N0 ek t ; t = 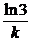 )
)
9. a) y′ + 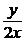 = x2, y(1) = 1; ( y = 5/(7
= x2, y(1) = 1; ( y = 5/(7 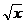 ) + 2x3/7)
) + 2x3/7)
b) 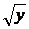 (2
(2 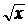 –
– 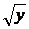 ) dx + x dy = 0, y(1) = 0; ( y = x ln2x)
) dx + x dy = 0, y(1) = 0; ( y = x ln2x)
c) Некоторое вещество преобразуется в другое вещество со скоростью, пропорциональной массе непреобразованного вещества. Если масса первого есть 31,4 г по истечении одного часа и 9,7 г по истечении трех часов, то определить через сколько времени после начала процесса останется лишь 1% первоначальной массы исходного вещества. (7,84 ч)
10. a) 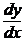 –
– 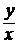 (1 + ln y – ln x) =0, y(1) = e; ( y = x ex)
(1 + ln y – ln x) =0, y(1) = e; ( y = x ex)
b) 3y′ + 2 xy = 2x y –2 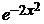 , y(0) = –1; ( y =
, y(0) = –1; ( y = 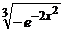 )
)
c) Некоторое вещество преобразуется в другое вещество со скоростью, пропорциональной массе непреобразованного вещества. Если масса первого есть 31,4 г по истечении одного часа и 9,7 г по истечении трех часов, то определить массу вещества в начале процесса.
(56,5 г)
11. a) y′ – 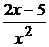 y = 5, y(2) =4; ( y = x2)
y = 5, y(2) =4; ( y = x2)
b) x dy = (x + y) dx, y(1) = 0; ( y = x lnx)
c) В баке находится 100 л раствора, содержащего 10 кг соли. В бак вливается вода со скоростью 5 л/мин, и смесь вытекает из него с той же скоростью. Однородность раствора достигается путем перемешивания. Сколько соли останется в баке через час? (0,5 кг)
12. a) (x2 – 3y2) dx + 2x y dy = 0, y(2) = 1; ( y = ± x 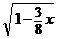 )
)
b) 3xy′ + 5y = (4x – 5) y4, y(1) = 1; ( y = 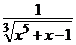 )
)
c) Состав замедляет свое движение под действием сопротивления, которое пропорционально скорости состава. Начальная скорость состава 1,5 м/с, скорость его через 4 секунды 1 м/с. Какой путь пройдет состав до остановки? (≈ 15 м)
13. a) y′ – 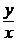 = –2
= –2 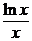 , y(1) = 1; ( y = 2lnx – x +2)
, y(1) = 1; ( y = 2lnx – x +2)
b) (x2 + y2 + xy) dx – x2 dy = 0, y(1) = 0; ( y = x tg lnx)
c) Состав замедляет свое движение под действием сопротивления, которое пропорционально скорости состава. Начальная скорость состава 1,5 м/с, скорость его через 4 секунды 1 м/с. Когда скорость уменьшится до 1 см/с? (≈ 50 с)
14. a) x2y′ + xy – x2 – y2 = 0, y(1) = 0; ( y = 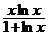 )
)
c) 3(xy′ + y) = x y2, y(1) = 3; ( y = 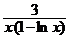 )
)
d) Скорость распада радия пропорциональна наличному его количеству. В течение года из каждого грамма радия распадается 0,44 мг. Через сколько лет распадется половина имеющегося количества радия? (Через 1575 лет)
15. a) x2 – 3y2 + 2 x y y′ =0, y(–2) = 2; ( y = –x)
b) y′ – y = 2x y 2, y(0) = 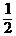 ; ( y =
; ( y = 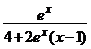 )
)
c) Скорость охлаждения тела пропорциональна разности температур тела и окружающей его среды (закон Ньютона). Найти зависимость температуры T от времени t, если тело, нагретое до
T0 = 100о С градусов, внесено в помещение, температура которого постоянна и равна a = 20оС. Через какое время температура тела опустится до 60 оС (принять k = 2 )? (T = a + (T0 – a) e –k t, t = ln 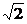 )
)
16. a) y′ = 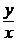 ln
ln 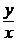 , y(1) = e; ( y = ex)
, y(1) = e; ( y = ex)
b) 2x y′ – 3y = –(20x 2 + 12) y3 , y(1) = 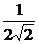 ; ( y =
; ( y = 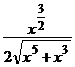 )
)
c) Через сколько времени температура тела, нагретого до 100оС, понизится до 25оС, если температура помещения равна 20оС и за первые 10 мин тело охладилось до 60оС? (Через 40 мин)
17. a) y′ – 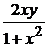 = 1 + x2, y(1) = 3; ( y =
= 1 + x2, y(1) = 3; ( y = 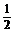 (x2+1) + x3+ x)
(x2+1) + x3+ x)
b) (2x – y) dx – x dy = 0, y(1) =1; ( y = x )
c) Ж/д состав движется со скоростью 20 км/час. Через одну минуту после выключения двигателя его скорость уменьшилась до 2 км/час. Определить скорость состава через две минуты после остановки двигателя, считая сопротивление движению пропорциональным скорости. (0,2 км/час)
18. a) y′ + 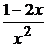 y = 1, y(1) = 1; ( y = x2)
y = 1, y(1) = 1; ( y = x2)
b) xy′ + y = y2ln x, y(1) =1; ( y = 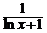 )
)
c) Тело движется по прямой со скоростью, обратно пропорциональной пройденному пути. В начальный момент тело имело скорость v0 = 15 м/с и находилось на расстоянии 4 м от начала отсчета пути. Определить скорость тела через 8 с после начала движения. ( 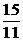 м/с)
м/с)
19. a) y′ + 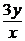 =
= 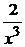 , y(1) = 1; ( y =
, y(1) = 1; ( y = 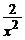 –
– 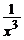 )
)
b) 2 y′ + 3y cos x = (8 + 12 cos x) e2x y –1 , y(0) = 2; ( y = 2ex )
c) Составить дифференциальное уравнение изменения скорости ж/д состава массы m = 10 000 тонн, движущегося со скоростью v0 = 10 м/с, при замедленном прямолинейном движении под действием силы сопротивления, пропорциональной квадрату скорости и равной 20000 Н при скорости 1 м/с. Определить какое расстояние пройдет состав после выключения двигателя, прежде чем его скорость уменьшится до 2 м/с .
(v´= – 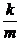 v2; 200 )
v2; 200 )
20. a) y′ +2xy =–2 x3, y(1) = e –1 ; ( y = 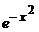 – x2 + 1 )
– x2 + 1 )
b) 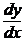 –
– 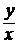 (1 + ln y – ln x) =0, y(1) = e; ( y = xex )
(1 + ln y – ln x) =0, y(1) = e; ( y = xex )
c) Скорость прироста населения страны пропорциональна его численности. Составить дифференциальное уравнение процесса изменения численности населения. Определить численность населения страны через 20 лет, зная что ее население в 2000 году составляло 145 млн человек, а прирост населения за 2000 год был равен –1% .
( 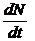 = kN ; N = 145 · (0.99)20 ≈ 119 млн человек )
= kN ; N = 145 · (0.99)20 ≈ 119 млн человек )
21. a) 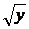 (2
(2 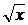 –
– 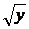 ) dx + x dy = 0, y(1) = 0; ( y = x ln2x )
) dx + x dy = 0, y(1) = 0; ( y = x ln2x )
b) 8xy′ – 12 y = –(5x2 + 3) y3, y(1) = 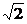 ; ( y =
; ( y = 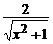 )
)
c) Скорость прироста населения страны пропорциональна его численности. Составить дифференциальное уравнение процесса изменения численности населения. Определить численность населения страны через 20 лет, зная что ее население в 2000 году составляло 145 млн человек, а прирост населения за 2000 год был равен 2% .
( 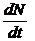 = kN ; N = 145 · (1.02)20 ≈ 215 млн человек )
= kN ; N = 145 · (1.02)20 ≈ 215 млн человек )
22. a) y′ = 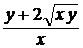 , y(1) = 0; ( y = x ln2x )
, y(1) = 0; ( y = x ln2x )
b) 2( y′ + y)= x y 2 , y(0) = 2; ( y = 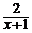 )
)
c) В благоприятных для размножения условиях находится некоторое количество N0 бактерий. Найти зависимость увеличения числа бактерий от времени, если скорость размножения бактерий пропорциональна их количеству. Через сколько времени количество бактерий увеличится втрое? (N = N0 ek t ; t = 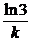 )
)
23. a) xy′ – y (lny – lnx) = 0, y(–1) = –1; ( y = x e x+1)
b) y′ + xy = (x – 1) ex y2, y(0) =1; ( y = e–x )
c) Некоторое вещество преобразуется в другое вещество со скоростью, пропорциональной массе непреобразованного вещества. Если масса первого есть 31,4 г по истечении одного часа и 9,7 г по истечении трех часов, то определить через сколько времени после начала процесса останется лишь 1% первоначальной массы исходного вещества. (7,84 ч)
24. a) y′ = – 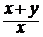 , y(1) = 0; ( y =
, y(1) = 0; ( y = 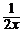 –
– 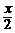 )
)
b) y′ + 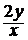 = y 2 x , y(1) = –1; ( y =
= y 2 x , y(1) = –1; ( y = 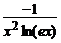 )
)
c) Некоторое вещество преобразуется в другое вещество со скоростью, пропорциональной массе непреобразованного вещества. Если масса первого есть 31,4 г по истечении одного часа и 9,7 г по истечении трех часов, то определить массу вещества в начале процесса.
(56,5 г)
25. a) (x 2 – 3 y 2 ) dx + 2xy dy = 0, y(2) = 1; ( y = 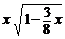 )
)
b) y′ – y = x y2, y(0) =1; ( y = 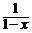 )
)
c) В баке находится 100 л раствора, содержащего 10 кг соли. В бак вливается вода со скоростью 5 л/мин, и смесь вытекает из него с той же скоростью. Однородность раствора достигается путем перемешивания. Сколько соли останется в баке через час? (0,5 кг)
26. a) y′ – y cos x =– sin 2x, y(0) = 3; ( y = e sinx+ 2sinx + 2)
b) xy′ – y + x 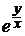 = 0, y(e) = 0; ( y = –x ln(lnx))
= 0, y(e) = 0; ( y = –x ln(lnx))
c) Состав замедляет свое движение под действием сопротивления, которое пропорционально скорости состава. Начальная скорость состава 1,5 м/с, скорость его через 4 секунды 1 м/с. Какой путь пройдет состав до остановки? (≈ 15 м)
27. a) y′ – 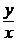 = –
= – 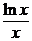 , y(1) = 1; ( y = lnx + 1)
, y(1) = 1; ( y = lnx + 1)
b) y′ = 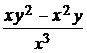 , y(–1) = 1; ( y =
, y(–1) = 1; ( y = 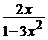 )
)
c) Состав замедляет свое движение под действием сопротивления, которое пропорционально скорости состава. Начальная скорость состава 1,5 м/с, скорость его через 4 секунды 1 м/с. Когда скорость уменьшится до 1 см/с? (≈ 50 с)
