Совместная система вида (1) может иметь одно или более решений.

Решения c₁⁽¹⁾, c₂⁽¹⁾, …, c_n⁽¹⁾ и c₁⁽²⁾, c₂⁽²⁾, …, c_n⁽²⁾ совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:

c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).

Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.

________________________________.

Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.

Пусть дана система линейных уравнений с n неизвестными (над произвольным полем):

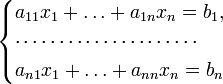
Тогда её можно переписать в матричной форме:

AX = B, где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:

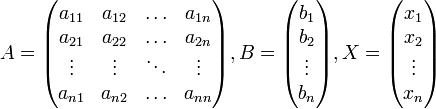
Умножим это матричное уравнение слева на A ^{− 1} — матрицу, обратную к матрице A: 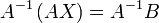(Поскольку A^-1A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A^-1B.)

Так как A ^{− 1}A = E, получаем X = A ^{− 1}B. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A:

.

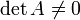Для однородной системы линейных уравнений, то есть когда вектор B = 0, действительно обратное правило: система AX = 0 имеет нетривиальное (то есть ненулевое) решение только еслиdet A = 0. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.

Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Назван по имени Габриэля Крамера (1704–1752), придумавшего метод.

Пусть дана система линейных уравнений

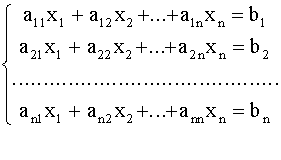(1)

Коэффициенты a₁₁,₁₂,..., a_1n, ... , a_n1 , b₂ , ... , b_n считаются заданными .

Вектор -строка íx₁ , x₂ , ... , x_n

ý - называется решением системы (1), если при подстановке этих чисел

Вместо переменных все уравнения системы (1) обращаются в верное равенство.

Определитель n-го порядка D=çAê=ça _ij

ç, составленный из коэффициентов при неизвестных , называется

Определителем системы (1). В зависимости от определителя системы (1) различают

Следующие случаи.

a). Если D¹0, то система (1) имеет единственное решение, которое может

быть найдено по формулам Крамера : x₁=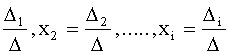

, где

определитель n-го порядка D_i ( i=1,2,...,n) получается из

определителя системы путем замены i-го столбца свободными членами b₁

, b₂ ,..., b_n.

б). Если D=0 , то система (1) либо имеет бесконечное множество решений , либо

Несовместна ,т.е. решений нет.

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

__________________________________________