Определение непрерывности в терминах приращений аргумента и функции
Определение непрерывности можно также сформулировать, используя приращения аргумента и функции. Функция является непрерывной в точке x = a, если справедливо равенство
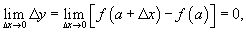
где 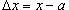 .
.
Приведенные определения непрерывности функции эквивалентны на множестве действительных чисел.
Функция является непрерывной на данном интервале, если она непрерывна в каждой точке этого интервала.
Связь между непрерывностью и дифференцируемостью функции. Если функция f ( x ) дифференцируема в некоторой точке, то она непрерывна в этой точке. Обратное неверно: непрерывная функция может не иметь производной.
С л е д с т в и е . Если функция разрывна в некоторой точке, то она не имеет производной в этой точке.
| П р и м е р . | Функция y = | x | ( рис.3 ) всюду непрерывна, но она не имеет производной при x = 0 , так как в этой точке не существует касательной к графику этой функции. ( Подумайте, почему ? ) |
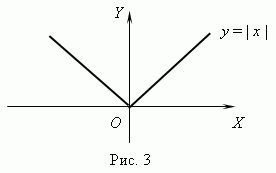
Достаточные признаки монотонности функции.
Если f ’( x ) > 0 в каждой точке интервала ( a, b ), то функция f ( x ) возрастает на этом интервале.
Если f ’( x ) < 0 в каждой точке интервала ( a, b ) , то функция f ( x ) убывает на этом интервале.
Бескочная производная
Можно ввести также понятие бесконечной производной f  (x)=+
(x)=+ 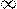
 f
f  (x)=−
(x)=− 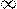
 f
f  (x)=
(x)= 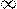
(последний случай может иметь место, если, например, lim 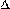 x
x 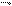 +0
+0 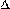 x
x 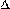 y=+
y=+ 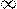
 lim
lim 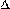 x
x 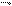 −0
−0 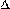 x
x 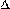 y=−
y=− 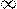 .
.
Если функция дифференцируема в точке x 0, то она непрерывна в этой точке.
Односторонние производные
Односторонние производные функции в точке.
Определение. Правой (левой) производной функции f(x) в точке х = х0 называется правое (левое) значение предела отношения 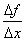 при условии, что это отношение существует.
при условии, что это отношение существует.
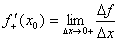
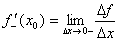
Если функция f(x) имеет производную в некоторой точке х = х0, то она имеет в этой точке односторонние производные. Однако, обратное утверждение неверно. Во- первых функция может иметь разрыв в точке х0, а во- вторых, даже если функция непрерывна в точке х0, она может быть в ней не дифференцируема.
Например: f(x) = ïxï- имеет в точке х = 0 и левую и правую производную, непрерывна в этой точке, однако, не имеет в ней производной.
Теорема. (Необходимое условие существования производной) Если функция f(x) имеет производную в точке х0, то она непрерывна в этой точке.
Понятно, что это условие не является достаточным.
Вопрос №17
Правила дифференцирования
Если с - постоянное число, и u = u(x), v = v(x) - некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
1) (с) ' = 0, (cu) ' = cu';
2) (u+v)' = u'+v';
3) (uv)' = u'v+v'u;
4) (u/v)' = (u'v-v'u)/v2;
5) если y = f(u), u = j(x), т.е. y = f(j(x)) - сложная функция, или суперпозиция, составленная из дифференцируемых функций j и f, то 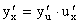 , или
, или
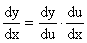 ;
;
6) если для функции y = f(x) существует обратная дифференцируемая функция x = g(y), причем 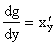 ≠ 0, то
≠ 0, то 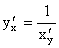 .
.
ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ
Пусть U=U(x) имеет производную в точке х, а y=f(x) имеет производную в соответствующей точке U=U(x), тогда сложная функции y=f(U(x)) также имеет производную в точке х.
Причем уштрих=(f(U(x)))штрих=fштрих(u)*Uштрих=yn*Ux .
Обратная проихзводная
Пусть дана функция f(x) для которой существует производная в точке х и для которой существует обратная функция х в -1= f в -1 (y), тогда ф-я f в -1 (y) имеет произволдную в точке х причем производная равна 1/fштрих(x) остальное на листе..
Логарифмическая произваодная
| Логарифмическая производная |
Логарифмическая производная – производная от натурального логарифма модуля (абсолютной величины) – данной функции: 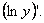 Используя формулу производной сложной функции, найдем, что Используя формулу производной сложной функции, найдем, что 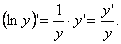 (*) Логарифмическую производную используют, например, при дифференцировании (нахождении производной или дифференциала) степенно-показательной функции. Пример Найдём производную функции у = хx. Поскольку lny= xlnx, легко найти логарифмическую производную: (*) Логарифмическую производную используют, например, при дифференцировании (нахождении производной или дифференциала) степенно-показательной функции. Пример Найдём производную функции у = хx. Поскольку lny= xlnx, легко найти логарифмическую производную: 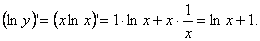 Теперь с помощью формулы (*) получим: Теперь с помощью формулы (*) получим: 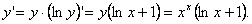 Логарифмическая производная функции имеет экономический смысл – отношение скорости изменения величины у (ее производной) к самой этой величине – темп изменения у; если темп положителен – скорость изменения увеличивается, если отрицателен – скорость падает. Логарифмическая производная функции имеет экономический смысл – отношение скорости изменения величины у (ее производной) к самой этой величине – темп изменения у; если темп положителен – скорость изменения увеличивается, если отрицателен – скорость падает. |
Вывод отстутсвует)
Вопрос №18
Теорема Лагранжа
Пусть:
1) f(x) определена и непрерывна в замкнутом промежутке [а,b],
2) существует конечная производная f/(x), по крайней мере, в открытом промежутке (а,b). Тогда между aи b найдется такая точка с(a< с <b), что для нее выполняется равенство
b−af(b)−f(a)=f/(c).
ДоказательствоВведем вспомогательную функцию, определив ее в промежутке [а,b] равенством:
F(x)=f(x)−f(a)−b−af(b)−f(a)(x−a).
Эта функция удовлетворяет всем условиям теоремы Ролля. В самом деле, она непрерывна в [а,b], так как представляет собой разность между непрерывной функцией f(x) и линейной функцией. В промежутке (а,b)она имеет определенную конечную производную, равную
F/(x)=f/(x)−b−af(b)−f(a).
Наконец, непосредственной подстановкой убеждаемся в том, чтоF(a)=F(b)= 0, т. е. F(x) принимает равные значения на концах
промежутка.
Следовательно, к функции F(x) можно применитьтеорему Ролля и утверждать существование в (а,b)такой точки с, что F′(с)=0.
Таким образом,
f/(c)−b−af(b)−f(a)=0,
откуда
b−af(b)−f(a)=f/(c).
Теорема доказана.
Обращаясь к геометрическому истолкованию теоремы Лагранжа, заметим, что отношение
b−af(b)−f(a)=CBAC
есть угловой коэффициент секущей АВ, а f/(c)есть угловой коэффициент касательной к кривой y=f(x) в точке с абсциссой x=c. Таким образом, утверждениетеоремы Лагранжа равносильно следующему: на дуге АВ всегда найдется, по крайней мере, одна точка М, в которой касательная параллельна хорде АВ.
Правило Лопиталя - метод нахождения пределов функций, раскрывающий неопределённости вида 0 / 0 и 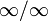 . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
Доказательство
Теорема 5.5 (Правило Лопиталя) Пусть функции 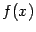 и
и 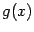 непрерывны в некоторой окрестности
непрерывны в некоторой окрестности 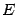 точки
точки 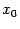 и
и 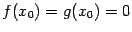 , то есть
, то есть 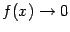 и
и 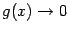 при
при 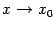 . Предположим, что при
. Предположим, что при 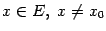 функции
функции 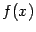 и
и 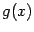 имеют производные
имеют производные 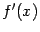 и
и 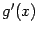 , причём существует предел отношения этих производных:
, причём существует предел отношения этих производных:
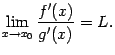
Тогда предел отношения самих функций 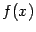 и
и 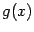 тоже существует и равен тому же числу
тоже существует и равен тому же числу 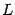 :
:
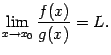
Доказательство. Заметим, что из условия 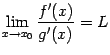 следует, что оба односторонних предела также равны
следует, что оба односторонних предела также равны 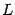 :
:
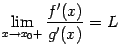 и
и 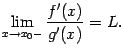
Пусть 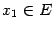 ,
, 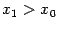 . По теореме Коши, применённой к отрезку
. По теореме Коши, применённой к отрезку 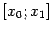 , получим тогда, с учётом того, что
, получим тогда, с учётом того, что 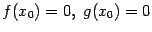 ,
,
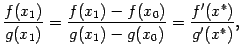
где 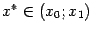 . Перейдём теперь в этом равенстве к пределу при
. Перейдём теперь в этом равенстве к пределу при 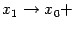 :
:
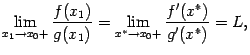
так как, очевидно, при 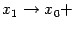 имеем также
имеем также 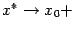 . Теперь возьмём точку
. Теперь возьмём точку 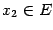 ,
, 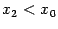 и применим теорему Коши к отрезку
и применим теорему Коши к отрезку 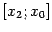 . Получим
. Получим
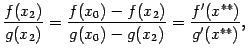
где 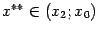 . Переходя к пределу при
. Переходя к пределу при 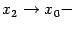 , получаем
, получаем
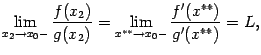
так как при 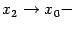 имеем
имеем 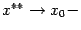 .
.
Итак, оба односторонних предела отношения 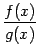 равны
равны 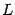 . На основании теоремы о связи односторонних пределов с двусторонним получаем, что
. На основании теоремы о связи односторонних пределов с двусторонним получаем, что
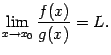
Вопрос №19
(Достаточное условие строгой монотонности функции, имеющей производную на интервале) Пусть функция 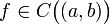 непрерывна на (a,b), и имеет в каждой точке
непрерывна на (a,b), и имеет в каждой точке 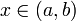 производную f'(x). Тогда
производную f'(x). Тогда
если 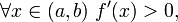 то f строго возрастает на (a,b);
то f строго возрастает на (a,b);
если 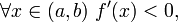 то f строго убывает на (a,b).
то f строго убывает на (a,b).
Пусть функция 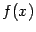 определена в некоторой окрестности
определена в некоторой окрестности 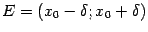 ,
, 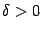 , некоторой точки
, некоторой точки 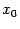 своей области определения. Точка
своей области определения. Точка 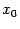 называется точкой локального максимума, если в некоторой такой окрестности
называется точкой локального максимума, если в некоторой такой окрестности 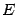 выполняется неравенство
выполняется неравенство 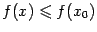 (
( 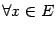 ), и точкой локального минимума, если
), и точкой локального минимума, если 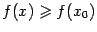
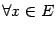 .
.
Понятия локальный максимум и локальный минимум объединяются терминомлокальный экстремум.
Необходимое условие локального экстремума дифференцируемой функции
Если 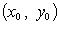 - точка экстремума функции f, то
- точка экстремума функции f, то
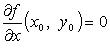 и
и 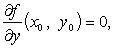 или
или 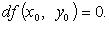
В самом деле, если мы допустим, что в точке x0 f′(x0)/=0 ,то по теореме 1 значение f(x0)не может быть локальным экстремумом, что противоречит условию теоремы. ч.т.д.
Первое достаточное условие. Пусть xо - критическая точка. Если f ¢ (x) при переходе через точку xо меняет знак плюс на минус, то в точке xо функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке xо экстремума нет.
Говорят, что функция 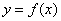 , определенная на промежутке Х, достигает на нем своего наибольшего (наименьшего) значения, если существует точка а, принадлежащая этому промежутку, такая, что для всех х из Х выполняется неравенство
, определенная на промежутке Х, достигает на нем своего наибольшего (наименьшего) значения, если существует точка а, принадлежащая этому промежутку, такая, что для всех х из Х выполняется неравенство 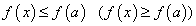 .
.
Функция, непрерывная на отрезке, достигает на нем своего наибольшего и наименьшего значений.
Наибольшее значение М и наименьшее значение m непрерывной функции могут достигаться как внутри отрезка, так и на его концах. Если наибольшего (наименьшего) значения функция достигает во внутренней точке отрезка, то эта точка является точкой экстремума.
Алгоритм отыскания наибольшего и наименьшего значений непрерывной функции 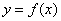 на отрезке
на отрезке 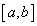 :
:
- найти
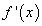 ;
; - найти точки, в которых
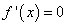 или
или 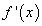 не существует, и отобрать из них те, что лежат внутри отрезка
не существует, и отобрать из них те, что лежат внутри отрезка 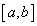 ;
; - вычислить значения функции
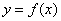 в точках, полученных в п.2, и на концах отрезка и выбрать из них наибольшее и наименьшее; они и будут соответственно наибольшим и наименьшим значениями функции
в точках, полученных в п.2, и на концах отрезка и выбрать из них наибольшее и наименьшее; они и будут соответственно наибольшим и наименьшим значениями функции 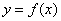 на отрезке
на отрезке 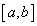 , которые можно обозначить так:
, которые можно обозначить так: 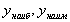 .
.
Если поставлена задача найти 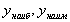 для непрерывной на
для непрерывной на 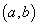 функции
функции 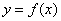 , то она решается по тому же правилу, что соответствующая задача для отрезка
, то она решается по тому же правилу, что соответствующая задача для отрезка 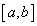 .
.
Отличие: на третьем этапе вместо вычисления значений функции на концах отрезка находят пределы функции при приближении к концам интервала.
Иногда для отыскания наибольшего или наименьшего значения непрерывной функции 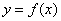 на промежутке
на промежутке 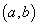 полезны два утверждения:
полезны два утверждения:
- если функция
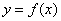 имеет в промежутке Х только одну точку экстремума
имеет в промежутке Х только одну точку экстремума 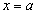 , причем это точка максимума, то
, причем это точка максимума, то 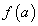 - наибольшее значение функции на промежутке Х;
- наибольшее значение функции на промежутке Х; - если функция
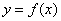 имеет в промежутке Х только одну точку экстремума
имеет в промежутке Х только одну точку экстремума 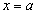 , причем это точка минимума, то
, причем это точка минимума, то 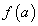 - наименьшее значение функции на промежуткеХ.
- наименьшее значение функции на промежуткеХ.
Вопрос №20
График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.
График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.
Теорема. Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x)отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f''(x) > 0 – вогнутый.
Второе достаточное условие
Если функция g(x) обладает второй производной 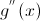 причем в некоторой точке
причем в некоторой точке 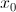 первая производная равна нулю, а вторая производная отлично от нуля. Тогда точка
первая производная равна нулю, а вторая производная отлично от нуля. Тогда точка 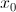 экстремум функции g(x), причем если
экстремум функции g(x), причем если 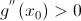 , то точка является максимумом; если
, то точка является максимумом; если 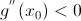 , то точка является минимумом.
, то точка является минимумом.
Точкой перегиба графика функции 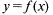 называется точка, в которой меняется направление выпуклости графика
называется точка, в которой меняется направление выпуклости графика
Точка перегиба функции 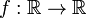 внутренняя точка x0 области определения f, такая что f непрерывна в этой точке, существует конечная или определенного знака бесконечная производная в этой точке, и x0 является одновременно концом интервала строгой выпуклости вверх и началом интервала строгой выпуклости вниз, или наоборот.
внутренняя точка x0 области определения f, такая что f непрерывна в этой точке, существует конечная или определенного знака бесконечная производная в этой точке, и x0 является одновременно концом интервала строгой выпуклости вверх и началом интервала строгой выпуклости вниз, или наоборот.
Необходимое условие существования точки перегиба: если функция f(x), дважды дифференцируемая в некоторой окрестности точки x0, имеет в x0 точку перегиба, то 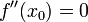 .
.
Достаточное условие точки перегиба: Точка x0 является точкой перегиба кривой если при переходе через эту точку вторая производная меняет свой знак
Вопрос №21
Прямая y=kx+b называется наклонной асимптотой графика функции y=f(x) тогда и только тогда когда существует конечные пределы k= lim f(x)/x х стремится к +- бесконечности
B=lim(f(x)-kx) x стертися к +- бесконечности. Причем асимптота называется правой(левой) при х стремящимся к +- бескосконечности.
Пример 7.6 Рассмотрим функцию 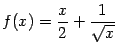 . График этой функции имеет наклонную асимптоту
. График этой функции имеет наклонную асимптоту 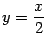 при
при 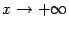 . Действительно,
. Действительно,
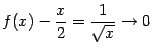 при
при 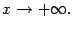
Однако эта функция не определена ни на каком луче вида 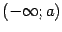 , так что её график не может иметь асимптоты при
, так что её график не может иметь асимптоты при 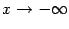 .
.
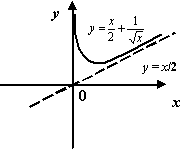
Рис.7.7.Наклонная асимптота функции 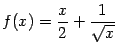
Пример 7.7 График функции 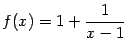 имеет горизонтальную асимптоту
имеет горизонтальную асимптоту 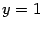 как при
как при 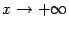 , так и при
, так и при 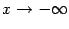 , поскольку, очевидно,
, поскольку, очевидно, 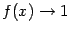 при
при 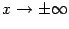 . Можно сказать также, что асимптота при
. Можно сказать также, что асимптота при 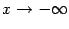 у этого графика совпадает с асимптотой при
у этого графика совпадает с асимптотой при 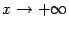 .
.
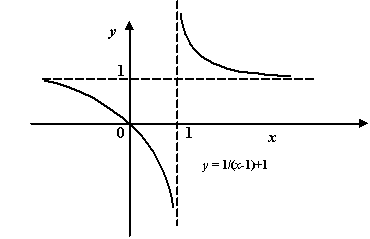
Рис.7.8.Горизонтальная асимптота функции 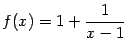
Определение 7.1 Вертикальной асимптотой графика функции 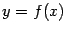 называется вертикальная прямая
называется вертикальная прямая 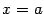 , если
, если 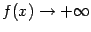 или
или 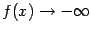 при каком-либо из условий:
при каком-либо из условий: 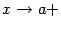 ,
, 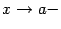 ,
, 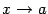 . Заметим, что мы при этом не требуем, чтобы точка
. Заметим, что мы при этом не требуем, чтобы точка 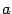 принадлежала области определения функции
принадлежала области определения функции 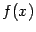 , однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки:
, однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки: 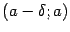 или
или 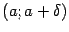 , где
, где 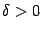 .
.
Пример 7.1 Рассмотрим функцию 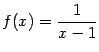 . График
. График 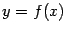 имеет вертикальную асимптоту
имеет вертикальную асимптоту 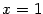 , поскольку при
, поскольку при 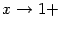 выполняется условие
выполняется условие 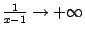 , а также при
, а также при 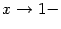 выполняется условие
выполняется условие 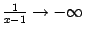 .
.
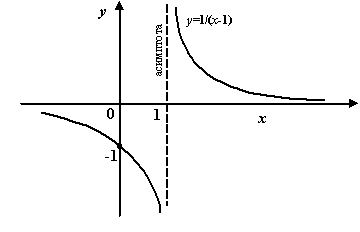
Рис.7.1.Вертикальная асимптота функции 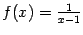
Пример 7.2 Рассмотрим функцию 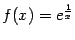 . Её график имеет вертикальную асимптоту
. Её график имеет вертикальную асимптоту 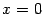 , так как
, так как 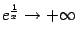 при
при 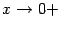 . То, что при
. То, что при 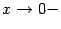 функция
функция 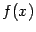 не стремится к бесконечности, для наличия асимптоты неважно: для того, чтобы прямая
не стремится к бесконечности, для наличия асимптоты неважно: для того, чтобы прямая 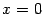 являлась вертикальной асимптотой, достаточно, чтобы график приближался к ней хотя бы с одной стороны. (К слову сказать,
являлась вертикальной асимптотой, достаточно, чтобы график приближался к ней хотя бы с одной стороны. (К слову сказать, 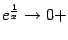 при
при 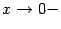 .)
.)
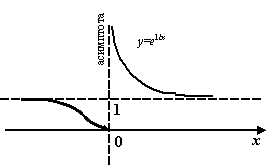
Рис.7.2.Вертикальная асимптота функции 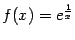
Пример 7.3 Рассмотрим функцию 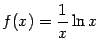 . Прямая
. Прямая 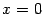 является вертикальной асимптотой графика
является вертикальной асимптотой графика 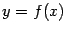 , так как
, так как 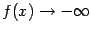 при
при 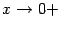 . Заметим, что слева от точки
. Заметим, что слева от точки 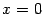 функция вообще не определена.
функция вообще не определена.
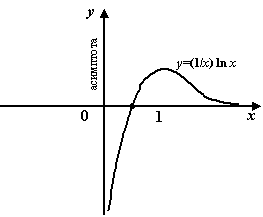
Рис.7.3.Вертикальная асимптота функции 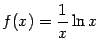
Пример 7.4 График функции 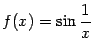 не имеет при
не имеет при 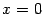 вертикальной асимптоты, так как
вертикальной асимптоты, так как 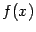 -- ограниченная (числом 1) и, следовательно, локально ограниченная при
-- ограниченная (числом 1) и, следовательно, локально ограниченная при 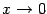 и не стремящаяся к бесконечности функция. Хотя аргумент синуса -- функция
и не стремящаяся к бесконечности функция. Хотя аргумент синуса -- функция 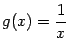 -- имеет вертикальную асимптоту
-- имеет вертикальную асимптоту 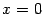 .
.
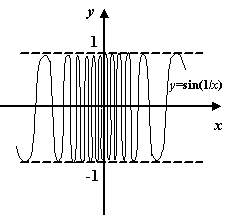
Рис.7.4.График функции 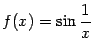 не имеет вертикальной асимптоты
не имеет вертикальной асимптоты
Пример 7.5 Прямая 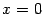 не является вертикальной асимптотой графика функции
не является вертикальной асимптотой графика функции 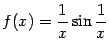 , поскольку здесь нельзя утверждать, что при
, поскольку здесь нельзя утверждать, что при 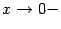 или
или 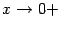 функция стремится к бесконечности. При некоторых малых значениях
функция стремится к бесконечности. При некоторых малых значениях 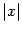 значения
значения 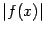 могут быть как угодно велики, однако при других малых
могут быть как угодно велики, однако при других малых 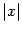 функция обращается в 0: так, при
функция обращается в 0: так, при 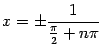 (
( 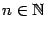 ) значения функции равны
) значения функции равны 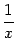 и стремятся к бесконечности при
и стремятся к бесконечности при 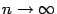 , а при всех
, а при всех 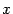 вида
вида 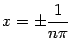 (
( 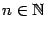 ) значения функции равны 0. В то же время как те, так и другие точки
) значения функции равны 0. В то же время как те, так и другие точки 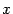 при увеличении
при увеличении 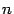 попадают всё ближе и ближе к точке 0. Значит, функция
попадают всё ближе и ближе к точке 0. Значит, функция 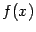 не является бесконечно большой при
не является бесконечно большой при 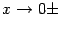 , и прямая
, и прямая 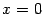 -- не асимптота.
-- не асимптота.
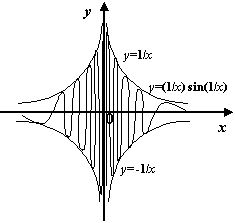
Рис.7.5.График функции 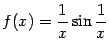 не имеет вертикальной асимптоты
не имеет вертикальной асимптоты
Схема построения графика
1) ОДЗ
2) выявить четность/нечетность y(-x)=y(x) y(-x)=-y(x)
3) найти точки пересечения графиков функции с осями координат
4) найти точки разрыва функции определить характер разрыва. Найти наклонные асимптоты
5) интервалы возрастания/убывания точки экстремума (1ая производная)
6) точки перегиба, интервалы выпуклости и вогнутости (вторая производная меньше нуля – выпуклая, наоорот-вогнутая)
7) посторить график функции
