Совместимость и нечеткое ожидание

В классической теории вероятностная система описывается тройкой ( 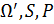), где 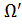- произвольное множество исходов, S – множество событий, P –вещественная функция, определенная 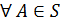и такая, что:

1) ;

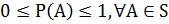2) P( 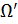) = 1;

3) Если A₁,A₂ ....A_n - любая последовательность попарно не пересекающихся множеств из 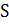, то:

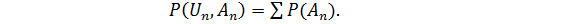(2.28)

Функция Р, удовлетворяющая этим трем условиям, называется вероятностной мерой, а элементы множества S- событиями.

Свойство 3) известно, как аксиома счетной аддитивности:

во-первых, событие может быть неточным, нечетким событием в том смысле, что оно принадлежит нечеткому множеству;

во-вторых, если A четкое, т.е. вполне определенное событие, функция P(A) может быть плохо определена, т.е., например: неясные оценки точных событий, расплывчатые предсказания.

Обсудим полноту вероятностной системы. Очевидно, что в конечных пространствах вероятность P(A) события A равна сумме вероятностей всех выборочных точек, составляющих множество A. Однако следует иметь в виду, что полнота классической структуры ограничивает каждую выборочную точку вполне определенным множеством. Поэтому в предлагаемых здесь мере и исчислении требование полноты, в конечном счете, не выполняется.

Среди теоретиков постоянно ведутся споры о природе соотношений между вероятностной математикой и теми событиями, в описании которых она применяется. Наиболее употребительным является частотный подход, основанный на эксперименте с повторяющимися испытаниями, в которых регистрируют отношения числа испытаний с желательным исходом к общему числу испытаний. Предельное значение этого отношения при неограниченном увеличении числа испытаний и считают вероятностью события. Если z- один элемент из полной группы несовместимых исходов, 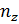- число испытаний с этим исходом, а n – общее число испытаний, то вероятность z равна:

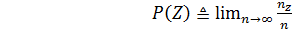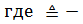, равно по определению. (2.29)

Если предела нет, то величина 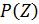считается неопределенной.

Одна из принципиальных трудностей частотного подхода состоит в том, что ситуации, которые случаются лишь однажды, в рамках этого подхода не имеют никакого смысла, т.к. для определения вероятности необходимы совокупности или последовательности событий. С этой точки зрения вероятность одиночного события, например, выпадение орла при конкретном бросании монеты должна быть либо неопределённой, либо равной 0 или 1, в зависимости от того, как падает монета. Аналогично, если последовательно придерживаться частотного подхода, то следует отвергнуть и априорные вероятности, поскольку они определяются не на основе испытаний, а из дополнительных соображений, например, по данным о числе граней игральной кости.

В рамках еще одного из известных подходов рассматривают меру того, в какой степени одно утверждение подтверждается другими утверждениями. Эта мера называется логической вероятностью. Она определена даже для ложных утверждений, поскольку описывает взаимосвязи между утверждениями, а не сами эти утверждения. Логический подход правомерен, когда ситуацию можно свести к множеству одинаково очевидных случаев.

В настоящее время, среди специалистов по принятию решений, устанавливается некоторый единый взгляд на вероятность, который явно допускает в ней наличие субъективной компоненты. Элемент человеческого суждения присутствует даже, казалось бы, в наиболее эффективных процедурах количественного определения вероятностей. При таком подходе не требуется, чтобы вероятность имела одно правильное значение, если это логически не очевидно. Суть субъективной точки зрения заключается в том, что вероятность тесно связана с индивидуальным принятием решения и отражает степень уверенности индивидуума в том, что данное событие действительно произойдёт. В этом смысле степень уверенности интерпретируется скорее как нечто, способствующее склонности к действию, а не как интенсивность ощущений (Бехтерева Н.П.), [43].

Некоторая субъективность присутствует и в частотном подходе, она связана с необходимостью предположения о существовании предела относительно частоты и с переоценкой вероятности, если для этого есть очевидные основания. Все это равносильно некоторому индивидуальному решению.

В каких случая стоит оценивать вероятность? Предполагается, что это необходимо, при наличии соответствующих данных, при этом их следует использовать для корректировки вероятностей, т.е., по существу, для количественного представления связанной с этим субъективной оценкой. Для описания этого процесса мы вводим понятие степень принадлежности, которая характеризует величину, зависящую от параметра подлежащего субъективной человеческой оценке. Следует отметить, что Сугэно М. [21] и Терано Т. [44] уже использовали нечеткие интегралы на отрезке [0,1], для представления своих оценок субъективных нечетких объектов. Кроме того, в настоящее время применяют это понятие для идентификации человеческих характеристик, а так же для макрооптимизации с использованием условных моделей и оценивания нечетких объектов.

Определение 4: Пусть B – борелевское поле ( 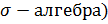подмножеств действительной числовой оси Ω.

Функция множеств 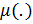, определенная на В, называется нечеткой мерой, если она удовлетворяет следующим условиям:

1.

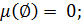
2.

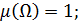
3. если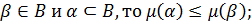

4. если { 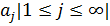} – монотонная последовательность, то .

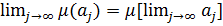Очевидно, что 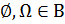, кроме того, если 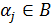, а { 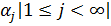} – монотонная последовательность, то .

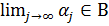Условия 1 и 2 означают, что нечеткая мера – ограниченная и отрицательная функции. Из условия 3 следует, что она монотонна (аналогично конечно-аддитивным мерам теории вероятностей), а из условия 4 следует непрерывность, если Ω - конечное множество, то непрерывность необязательна.

Определение 5: Система { 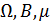} называется пространством с нечеткой мерой; ее аналогом в теории вероятностей служит система .

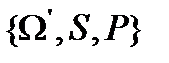Функция 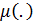называется нечеткой мерой на ( 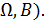Нечеткая мера определена на интервалах действительной оси. Ясно, что, если 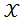- функция принадлежности множеству А, то для описания функции 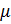[ 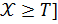необходимо использовать некоторую функцию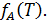

Далее рассматривается лишь случай, когда А – четко определенное множество, поэтому вместо 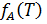будем использовать функцию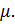

Пусть задано отображение 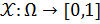и множество

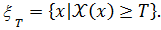
Функция 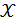- называется В-измеримой (или измеримой по Э.Борелю [18]), если 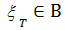при всех T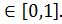

Определение 6: пусть 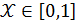- В-измеримая функция. Нечетким ожиданием FEV (fuzzyexpectedvalue) функции 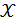на множестве А, по мере 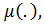называется Sup{min [T, ]}, .

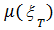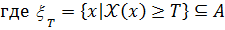Замечание 2: В-измеримая функция 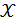называется функцией совместимости.

Нечеткое ограничение (разумеется, субъективное) описывается функцией совместимости 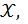которая каждому значению базовой переменной ставит в соответствие число из отрезка 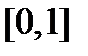, характеризующее совместимость этого значения с данным нечетким ограничением.

Контрольные вопросы и задания для самостоятельной работы по главам 1 и 2

2.1. Понятие знаний, место и роль, которую играют языки представления знаний в системах, основанных на использовании знаний?

2.2. Экспертная система-это интеллектуальная программа, способная делать логические выводы на основании знаний в конкретной предметной области?

2.3. Перечислите требования к экспертным системам, качествам экспертов и функции, которые должны выполнять структурные элементы экспертной системы?

2.4. Кто ввел понятие инженерии знаний и что такое язык представления знаний?

2.5. Каким образом представляются и используются знания в системах, основанных на концепциях искусственного интеллекта и инженерии знаний?

2.6. Каким образом и с помощью чего представляются модели представления знаний?

2.7. Как объяснить особенности преимуществ человеческой логики в построении интеллектуальных моделей с нечеткой структурой?

2.8. От чего зависит и каким образом происходят восприятие и обработка информации у человека. Что понимается под знанием?

2.9. Объясните основные методы и средства обработки, хранения, передачи и накопления знаний?

2.10. Как ВЫ понимаете и представляете обработку, хранение, передачу и накопление знаний?

2.11. Как ВЫ понимаете и представляете систему с базами знаний, основанные на совокупности правил вида «ЕСЛИ-ТО»?

2.12. Синтаксис и семантика логики первого порядка?

2.13. Теория нечетких множеств - основа псевдофизических логик?

2.14. Нечеткая логика?

2.15. Логика смысла?

2.16. Понятие лингвистической переменной?

2.17. Примеры псевдофизических логик: пространственная и временная логики (как средства представления пространственной и временной информации)?

2.18. Модели для логики первого порядка?

2.19. Использование логики первого порядка?

2.20. Инженерия знаний с применением логики первого порядка?

2.21. Классификациязадач анализа данных?

2.22. Базовые гипотезы, лежащие в основе методов анализа данных?

2.23. Статистические решающие правила?

2.24. Построение решающих правил по конечной выборке?

2.25. Выбор системы информативных признаков?

2.26. Согласование разнотипных шкал?

2.27. Распознавание образов в пространстве знаний?

2.28. Об анализе мер сходства?