Исследование линейных систем
Исследование линейных систем
В среде MATLAB/SIMULINK
Методические указания к лабораторным работам
по дисциплине «Теория управления»
Санкт-Петербург
Издательство СПбГЭТУ "ЛЭТИ"
УДК 519.71(075.9)
Исследование линейных систем в среде MATLAB/SIMULINK: Методические указания к лабораторным работам по дисциплине “Теория управления” / Сост.: А. А. Бурмистров, В. Б. Второв, И. А. Приходько, О. Э. Якупов. СПб.: Издательство СПбГЭТУ "ЛЭТИ", 2004. 24 с.
Содержат программы и методики выполнения лабораторных работ по анализу математических моделей систем автоматического управления на ЭВМ.
Предназначены для студентов направлений 550200, 551300, 652300, 651900, 652000, специальности 210500 и других специальностей факультета электротехники и автоматики.
Утверждено
редакционно-издательским советом университета
в качестве методических указаний
 © СПбГЭТУ "ЛЭТИ", 2004
© СПбГЭТУ "ЛЭТИ", 2004
Предисловие
Настоящие методические указания предназначены студентам, выполняющим лабораторный практикум по дисциплине "Теория управления" учебных планов подготовки бакалавров по направлениям 550200 "Автоматизация и управление", 551300 "Электротехника, электромеханика, электротехнологии" и инженеров по специальности 210500 "Системы управления летательными аппаратами" и ряду других специальностей факультета электротехники и автоматики СПбГЭТУ "ЛЭТИ".
Материал лабораторных работ охватывает широкий круг типовых задач анализа систем автоматического управления во временнόй, комплексной и частотных областях. Несколько последних работ направлены на углубление понимания студентами некоторых методов синтеза автоматических систем.
Предполагается, что все работы выполняются на персональном компьютере с использованием системы моделирования MATLAB / SIMULINK или другого пакета, позволяющего осуществлять математическое моделирование динамических систем.
Описание каждой лабораторной работы начинается с краткого изложения основных сведений, необходимых для ее выполнения, и заканчивается контрольными вопросами для самопроверки. В зависимости от технических возможностей лабораторной базы и простой целесообразности иллюстративный материал, включаемый студентами в свои отчеты, может содержать как твердые копии экрана, так и выполненные от руки эскизы.
Лабораторная работа №1
ИССЛЕДОВАНИЕ ДИНАМИЧЕСКИХ СВОЙСТВ ТИПОВЫХ ЗВЕНЬЕВ САУ ВО ВРЕМЕННОЙ И ЧАСТОТНОЙ ОБЛАСТЯХ
Цель работы – анализ переходных и частотных характеристик важнейших типовых звеньев систем автоматического управления.
Основные сведения
Переходная характеристика (ПХ) динамического звена (или системы) – это его реакция 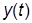 на единичное ступенчатое входное воздействие
на единичное ступенчатое входное воздействие 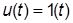 при нулевых начальных условиях (ННУ). Для ПХ обычно используют специальное обозначение
при нулевых начальных условиях (ННУ). Для ПХ обычно используют специальное обозначение 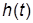 . Передаточной функцией (ПФ) звена называют отношение изображения по Лапласу выходной и входной переменных этого звена при ННУ:
. Передаточной функцией (ПФ) звена называют отношение изображения по Лапласу выходной и входной переменных этого звена при ННУ: 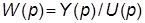 .
.
Частотная передаточная функция (ЧПФ) 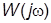 получается из ПФ подстановкой
получается из ПФ подстановкой 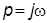 . Годограф функции
. Годограф функции 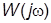 при изменении аргумента
при изменении аргумента 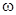 от
от 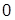 до
до 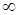 называется амплитудно-фазовой частотной характеристикой (АФХ). Если ЧПФ представлена в показательной форме
называется амплитудно-фазовой частотной характеристикой (АФХ). Если ЧПФ представлена в показательной форме 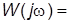
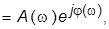 то функции
то функции 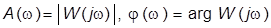 называются, соответственно, амплитудной (АЧХ) и фазовой (ФЧХ) частотными характеристиками. Они характеризуют поведение устойчивого звена (системы) в установившемся режиме при гармоническом входном воздействии и могут быть определены экспериментально. Для этого на вход исследуемого звена необходимо подавать гармоническое воздействие постоянной амплитуды и различной частоты. Тогда установившаяся реакция звена на это воздействие будет также гармонической функцией той же частоты, но, вообще говоря, другой амплитуды и с фазовым сдвигом относительно входной гармоники. Отношение амплитуд выходной и входной гармоник на каждой заданной частоте равно значению АЧХ, а относительный фазовый сдвиг этих функций – значению ФЧХ на указанной частоте.
называются, соответственно, амплитудной (АЧХ) и фазовой (ФЧХ) частотными характеристиками. Они характеризуют поведение устойчивого звена (системы) в установившемся режиме при гармоническом входном воздействии и могут быть определены экспериментально. Для этого на вход исследуемого звена необходимо подавать гармоническое воздействие постоянной амплитуды и различной частоты. Тогда установившаяся реакция звена на это воздействие будет также гармонической функцией той же частоты, но, вообще говоря, другой амплитуды и с фазовым сдвигом относительно входной гармоники. Отношение амплитуд выходной и входной гармоник на каждой заданной частоте равно значению АЧХ, а относительный фазовый сдвиг этих функций – значению ФЧХ на указанной частоте.
Функция 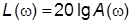 называется логарифмической амплитудной частотной характеристикой (ЛАХ) и графически изображается как функция частоты
называется логарифмической амплитудной частотной характеристикой (ЛАХ) и графически изображается как функция частоты 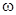 , рад/c, откладываемой по оси абсцисс в логарифмическом масштабе, т. е. фактически как функция безразмерной переменной
, рад/c, откладываемой по оси абсцисс в логарифмическом масштабе, т. е. фактически как функция безразмерной переменной 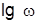 , откладываемой в равномерном масштабе. Значения
, откладываемой в равномерном масштабе. Значения 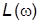 измеряются в децибелах (дБ) и откладываются по оси ординат в равномерном масштабе. ФЧХ, изображаемая как функция частоты, откладываемой в логарифмическом масштабе, называется логарифмической фазовой частотной характеристикой (ЛФХ). Ее значения измеряются в градусах или радианах. ЛАХ и ЛФХ называются логарифмическими частотными характеристиками (ЛЧХ).
измеряются в децибелах (дБ) и откладываются по оси ординат в равномерном масштабе. ФЧХ, изображаемая как функция частоты, откладываемой в логарифмическом масштабе, называется логарифмической фазовой частотной характеристикой (ЛФХ). Ее значения измеряются в градусах или радианах. ЛАХ и ЛФХ называются логарифмическими частотными характеристиками (ЛЧХ).
Программа работы
1. Задать интегрирующее звено с передаточной функцией 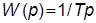 , взяв значение
, взяв значение 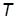 из табл. 1.1 (номер варианта задает преподаватель).
из табл. 1.1 (номер варианта задает преподаватель).
2. Выполнить анализ характеристик звена и ответить на приведенные вопросы.
а) Чему равно значение ПХ 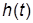 при
при 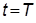 ?
?
б) Что представляют собой графики ЛАХ и ЛФХ ?
в) На какой частоте ЛАХ пересекает ось абсцисс ?
г) Как изменятся ПХ и ЛАХ при увеличении значения 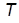 вдвое ?
вдвое ?
3. Задать апериодическое звено первого порядка с ПФ 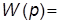
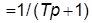 , взяв то же значение
, взяв то же значение 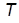 , что и в п. 1.
, что и в п. 1.
4. По результатам анализа ответить на приведенные вопросы.
а) Чему равно значение 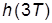 ?
?
б) Каков полюс ПФ ?
в) Каковы значения ЛАХ и ЛФХ на частотах 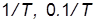 и
и 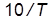 ?
?
г) Как изменятся значения ПХ и ЛЧХ при уменьшении значения 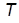 в 2 раза ? Что при этом произойдет с АФХ ?
в 2 раза ? Что при этом произойдет с АФХ ?
д) Как изменятся значения ПХ и ЛЧХ при увеличении коэффициента передачи в 2 раза ?
5. Задать неустойчивое апериодическое звено первого порядка с ПФ 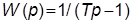 , назначив значение
, назначив значение 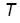 в соответствии с п. 1.
в соответствии с п. 1.
6. На основании анализа ПХ, ЛАХ, ЛФХ, АФХ, полюса ПФ дать характеристику различий в свойствах звеньев, заданных в пп. 3 и 5.
7. Задать колебательное звено с ПФ 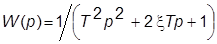 с параметрами из табл. 1.1.
с параметрами из табл. 1.1.
Таблица 1.1
| Параметр | Вариант | |||||||||
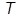 , с , с | 0.1 | 0.2 | 0.25 | 0.4 | 0.5 | 0.8 | 1.0 | 1.25 | 1.6 | 2.0 |
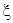 | 0.4 | 0.3 | 0.25 | 0.2 | 0.1 | 0.08 | 0.06 | 0.05 | 0.04 | 0.03 |
8. Выполнить анализ характеристик звена и ответить на приведенные вопросы.
а) Как влияет на показатель качества ПХ (максимальное значение, длительность переходного процесса, период колебаний) уменьшение коэффициента затухания 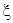 в 5 раз по сравнению с заданным?
в 5 раз по сравнению с заданным?
б) Как повлияет на эти же показатели уменьшение постоянной времени 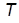 в 2 раза ?
в 2 раза ?
в) Как меняется картина расположения полюсов передаточной функции при изменении 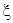 и
и 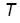 ?
?
г) Что происходит с высотой резонансного пика ЛАХ при уменьшении 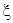 и с резонансной частотой
и с резонансной частотой 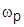 при уменьшении
при уменьшении 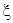 ?
?
9. Увеличить значение 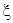 до произвольного значения, большего или равного единице, превратив тем самым звено в апериодическое звено второго порядка. Описать изменения, произошедшие с ПХ и с расположением полюсов на комплексной плоскости.
до произвольного значения, большего или равного единице, превратив тем самым звено в апериодическое звено второго порядка. Описать изменения, произошедшие с ПХ и с расположением полюсов на комплексной плоскости.
10. Определить путем имитации реального эксперимента значения АЧХ (ЛЧХ) и ФЧХ (ЛФХ) апериодического звена (значение 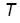 взять из табл.1.1) при трех значениях частоты
взять из табл.1.1) при трех значениях частоты 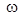 :
: 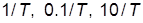 . Рекомендуется воспользоваться следующей последовательностью действий:
. Рекомендуется воспользоваться следующей последовательностью действий:
· на вход исследуемого звена подать гармонический сигнал единичной амплитуды и заданной частоты;
· определить амплитуду выходного сигнала 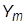 и его временной сдвиг
и его временной сдвиг 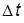 относительно входного; указанные измерения следует производить по прошествии интервала времени не менее
относительно входного; указанные измерения следует производить по прошествии интервала времени не менее 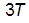 , когда наблюдаемый на выходе звена процесс можно считать установившимся; удобно совместить в одном окне входной и выходной процессы с помощью мультиплексора;
, когда наблюдаемый на выходе звена процесс можно считать установившимся; удобно совместить в одном окне входной и выходной процессы с помощью мультиплексора;
· определить значения АЧХ и ФЧХ как 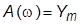 и
и 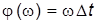 , а также вычислить
, а также вычислить 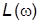 ;
;
· полученные для каждого значения частоты данные занести в таблицу.
11. Описанным в предыдущем пункте способом определить значения АЧХ (ЛЧХ) и ФЧХ (ЛФХ) колебательного звена с параметрами, взятыми из табл. 1.1, при указанных значениях частоты.
Содержание отчета
1. Ответы на вопросы, содержащиеся в программе работы.
2. Результаты экспериментального определения АЧХ и ФЧХ (и, соответственно, ЛЧХ и ЛФХ) апериодического и/или колебательного звеньев. Изобразить теоретические графики асимптотических ЛАХ рассматриваемых звеньев и нанести на них точки, определенные экспериментально, а также в 4, в). Прокомментировать результаты.
Контрольные вопросы
1. Дайте определения передаточной функции, частотной передаточной функции, АЧХ, ФЧХ, ЛАХ, ЛФХ звена (системы).
2. Каков "физический смысл" АЧХ и ФЧХ (с точки зрения реакции на гармоническое воздействие)?
3. Зависит ли точность экспериментального определения АЧХ и ФЧХ от интервала наблюдения?
4. Выведите аналитические выражения для переходных характеристик интегрирующего и апериодического звеньев.
5. Каков "физический смысл" постоянной времени интегрирующего звена?
6. Укажите максимальное число способов определения постоянной времени апериодического звена по графику его переходной характеристики.
7. Как связаны полюсы ПФ колебательного звена с поведением огибающей его переходной характеристики и частотой колебаний?
8. Выведите аналитическую зависимость между значением ЛАХ колебательного звена на частоте 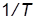 и коэффициентом затухания
и коэффициентом затухания 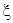 .
.
Лабораторная работа № 2
АВТОМАТИЧЕСКИХ СИСТЕМ
Цель работы– изучение влияния изменения параметров системы на показатели качества и на характер протекающих в системе процессов.
Основные сведения
Важнейшими показателями качества (ПК) переходной характеристики (ПХ) 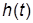 , или прямыми показателями качества системы являются:
, или прямыми показателями качества системы являются:
· время регулирования 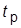 – время, по истечении которого ПХ не выходит из области допустимых (обычно пятипроцентных) отклонений от установившегося значения (УЗ)
– время, по истечении которого ПХ не выходит из области допустимых (обычно пятипроцентных) отклонений от установившегося значения (УЗ) 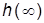 :
: 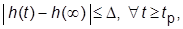 где
где 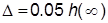 ;
;
· время нарастания 
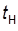 – время первого достижения УЗ;
– время первого достижения УЗ;
· перерегулирование 
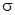 – превышение максимума ПХ над УЗ в процентах от УЗ:
– превышение максимума ПХ над УЗ в процентах от УЗ: 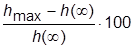 .
.
Среди косвенных ПК систем автоматического управления широко употребляются частотные и корневые.
Некоторые частотные ПК:
· частота среза 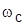 – частота, при которой ЛАХ разомкнутой системы пересекает ось абсцисс:
– частота, при которой ЛАХ разомкнутой системы пересекает ось абсцисс: 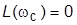 ; служит мерой быстродействия системы;
; служит мерой быстродействия системы;
· запас устойчивости по фазе 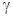 – превышение ЛФХ разомкнутой системы на частоте среза над уровнем –
– превышение ЛФХ разомкнутой системы на частоте среза над уровнем – 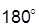 (в устойчивой системе):
(в устойчивой системе): 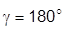 + +
+ + 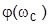 ; с уменьшением
; с уменьшением 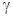 переходные процессы становятся более колебательными;
переходные процессы становятся более колебательными;
· полоса пропускания 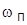 – частота, при которой значение АЧХ замкнутой системы в
– частота, при которой значение АЧХ замкнутой системы в 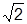 раз меньше ее значения на нулевой частоте:
раз меньше ее значения на нулевой частоте: 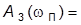
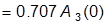 или
или 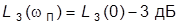 ; является мерой быстродействия системы;
; является мерой быстродействия системы;
· показатель колебательности 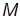 – отношение максимального значения АЧХ замкнутой системы к начальному значению:
– отношение максимального значения АЧХ замкнутой системы к начальному значению: 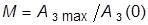 ; характеризует склонность системы к колебаниям.
; характеризует склонность системы к колебаниям.
Основные корневые ПК:
· степень устойчивости 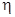 – расстояние от мнимой оси до ближайшего корня (или пары комплексно-сопряженных корней) характеристического полинома (ХП) замкнутой системы; является мерой быстродействия; если ПФ не имеет нулей, то при увеличении действительной и мнимой частей каждого полюса в
– расстояние от мнимой оси до ближайшего корня (или пары комплексно-сопряженных корней) характеристического полинома (ХП) замкнутой системы; является мерой быстродействия; если ПФ не имеет нулей, то при увеличении действительной и мнимой частей каждого полюса в  раз длительность переходного процесса сократится также в
раз длительность переходного процесса сократится также в  раз;
раз;
· колебательность 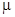 – отношение модулей мнимой и вещественной частей ближайшей к мнимой оси пары комплексных корней ХП; чем больше
– отношение модулей мнимой и вещественной частей ближайшей к мнимой оси пары комплексных корней ХП; чем больше 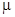 , тем меньше затухание колебаний за период.
, тем меньше затухание колебаний за период.
Некоторые способы суждения об устойчивости системы:
· для асимптотической устойчивости необходимо и достаточно, чтобы все корни ХП располагались в левой полуплоскости; если один корень находится в начале координат или одна пара корней – на мнимой оси (остальные – в левой полуплоскости), то система находится на границе устойчивости – соответственно, апериодического или колебательного типа);
· в асимптотически устойчивой системе все коэффициенты ХП положительны; если хотя бы один из коэффициентов ХП отрицателен, система неустойчива;
· согласно критерию Гурвица, для асимптотической устойчивости системы третьего порядка с положительными коэффициентами ХП необходимо и достаточно, чтобы произведение двух средних коэффициентов было больше произведения двух крайних коэффициентов (для колебательной границы устойчивости имеет место равенство этих произведений);
· согласно критерию Найквиста, если ПФ разомкнутой системы имеет полюсы только в левой полуплоскости (кроме, возможно, одного нулевого), то для асимптотической устойчивости замкнутой системы необходимо и достаточно, чтобы при изменении частоты от нуля до бесконечности АФХ разомкнутой системы не охватывала точку с координатами (–1, j0), или, что то же самое, чтобы разность между числом положительных (сверху вниз) и отрицательных (снизу вверх) переходов АФХ через луч ( 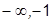 ] равнялась нулю; в терминах ЛЧХ это соответствует тому, что в диапазоне частот, где ЛАХ разомкнутой системы лежит выше оси, разность между числом положительных (снизу вверх) и отрицательных (сверху вниз) переходов ЛФХ через горизонтальную прямую с ординатой
] равнялась нулю; в терминах ЛЧХ это соответствует тому, что в диапазоне частот, где ЛАХ разомкнутой системы лежит выше оси, разность между числом положительных (снизу вверх) и отрицательных (сверху вниз) переходов ЛФХ через горизонтальную прямую с ординатой 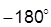 равняется нулю.
равняется нулю.
Программа работы
Работа рассчитана на два занятия: программа первого включает задания 2.2.1 и 2.2.2, второго – 2.2.3.
2.2.1. Исследование влияния контурного коэффициента
усиления системы на ее динамические свойства
1. Задать структурную схему системы третьего порядка, составленную из последовательно соединенных звеньев с ПФ 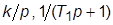 и
и 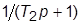 , охваченных единичной отрицательной обратной связью. Назначить
, охваченных единичной отрицательной обратной связью. Назначить 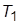 в соответствии с нижеприведенными вариантами и задать
в соответствии с нижеприведенными вариантами и задать 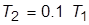 :
:
| Вариант | ||||||||||
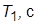 | 1.0 | 0.1 | 2.0 | 0.2 | 2.5 | 0.25 | 0.8 | 0.5 | 0.4 | 4.0 |
2. Для значений  , равных
, равных 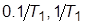 и
и 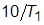 , определить и занести в таблицу значения
, определить и занести в таблицу значения 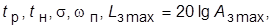 корней ХП,
корней ХП, 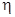 и
и 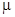 . Описать изменение характера переходного процесса с увеличением
. Описать изменение характера переходного процесса с увеличением  .
.
3. Увеличить  до значения
до значения 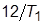 . Ответить на вопросы: каким стал переходный процесс? какие изменения произошли с корнями ХП?
. Ответить на вопросы: каким стал переходный процесс? какие изменения произошли с корнями ХП?
4. Разомкнуть обратную связь. Для значений  , указанных в пп. 2 и 3, определить и занести в таблицу
, указанных в пп. 2 и 3, определить и занести в таблицу 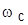 и (только для первых трех значений
и (только для первых трех значений  )
) 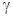 , а также исследовать с позиций критерия Найквиста изменения, происходящие в АФХ и ЛЧХ с ростом
, а также исследовать с позиций критерия Найквиста изменения, происходящие в АФХ и ЛЧХ с ростом  .
.
2.2.2. Исследование влияния относительной инерционности
звеньев системы на ее устойчивость
5. В предыдущей схеме, но с замкнутой обратной связью и со значением  , назначенном в п. 3, уменьшить
, назначенном в п. 3, уменьшить 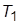 в 4 раза. Описать изменения, произошедшие в характере переходного процесса и в расположении корней ХП.
в 4 раза. Описать изменения, произошедшие в характере переходного процесса и в расположении корней ХП.
6. Задать структурную схему системы, состоящей из трех последовательно соединенных апериодических звеньев с постоянными времени 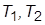 и
и 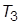 , охваченных единичной отрицательной обратной связью. Одно из звеньев имеет коэффициент передачи
, охваченных единичной отрицательной обратной связью. Одно из звеньев имеет коэффициент передачи  , остальные – единичный.
, остальные – единичный.
7. Назначить 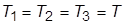 , где
, где 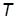 – произвольная константа. Подобрать такое значение
– произвольная константа. Подобрать такое значение 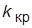 контурного коэффициента
контурного коэффициента  , при котором система выйдет на колебательную границу устойчивости, т. е. ПХ примет вид незатухающих колебаний. Определить частоту
, при котором система выйдет на колебательную границу устойчивости, т. е. ПХ примет вид незатухающих колебаний. Определить частоту 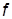 , Гц, этих колебаний.
, Гц, этих колебаний.
8. Назначить 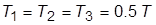 . Снова определить
. Снова определить 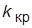 и
и 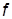 , сравнить их с предыдущими значениями.
, сравнить их с предыдущими значениями.
9. Оставив 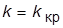 , задать новое соотношение постоянных времени:
, задать новое соотношение постоянных времени: 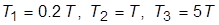 . Охарактеризовать изменения, произошедшие в свойствах системы. Увеличением
. Охарактеризовать изменения, произошедшие в свойствах системы. Увеличением  определить новое значение
определить новое значение 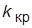 .
.
10. По результатам исследований в пп. 5–9 ответить на вопрос: какие факторы – абсолютные значения постоянных времени или их соотношения – влияют на устойчивость, характер переходных процессов в системе и на ее критический коэффициент усиления ?
2.2.3. Изучение стандартных полиномов
и диаграммы Вышнеградского
11. Задать структурную схему системы третьего порядка в управляемой канонической форме (рисунок).
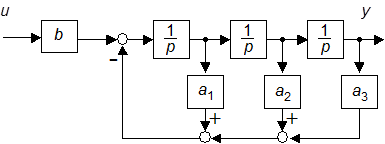
12. Задать систему с единичным коэффициентом передачи и ХП Баттерворта, для чего назначить 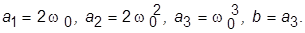 Значение
Значение 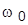 взять из приведенных ниже:
взять из приведенных ниже:
| Вариант | ||||||||||
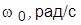 | 2,5 |
13. Определить корни ХП и установить закономерность их геометрического расположения на комплексной плоскости. Определить 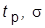 и
и 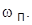
14. Повторить анализ, увеличив 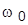 в 2 раза.
в 2 раза.
15. Задать систему с биномиальным ХП, назначив 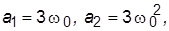
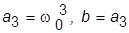 (оставить первоначальное значение
(оставить первоначальное значение 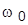 ) и повторить п. 13.
) и повторить п. 13.
16. Задать звено с ПФ 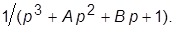
| Параметр | Номер опыта | |||||
| A | 0.5 | |||||
| B | 0.5 |
17. Последовательно задавать комбинации значений параметров Вышнеградского 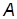 и
и 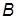 согласно таблице. Для каждого из сочетаний определить полюсы ПФ и описать характер ПХ.
согласно таблице. Для каждого из сочетаний определить полюсы ПФ и описать характер ПХ.
Содержание отчета
1. Структурные схемы и численные значения их параметров.
2. Результаты по каждому пункту программы работы и комментарии к ним. Ответы на вопросы, содержащиеся в программе работы.
3. Вычисление критических значений контурного коэффициента в заданиях 2.2.1 и 2.2.2 исходя из условия нахождения системы на границе устойчивости (по критерию Гурвица). 
4. Графики зависимости 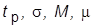 и
и 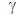 от
от  . При определении
. При определении 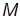 учесть, что
учесть, что 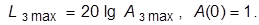 (Прокомментировать графики, изобразив по ПФ (см. начало программы работы) асимптотические ЛАХ разомкнутой системы при различных
(Прокомментировать графики, изобразив по ПФ (см. начало программы работы) асимптотические ЛАХ разомкнутой системы при различных 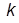 и (эскизно) ЛФХ.)
и (эскизно) ЛФХ.)
5. Значения корней стандартных полиномов и значения 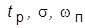 с анализом влияния на них значения
с анализом влияния на них значения 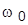 и пояснением связи характера ПХ с картиной расположения корней на плоскости.
и пояснением связи характера ПХ с картиной расположения корней на плоскости.
6. Эскиз диаграммы Вышнеградского с нанесенными на нее точками, определяющими заданные в таблице на с. 11 сочетания параметров 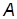 и
и 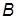 ; вывод о связи характера ПХ с полюсами ПФ.
; вывод о связи характера ПХ с полюсами ПФ.
Для построения диаграммы необходимо:
· изобразить систему координатных осей для параметров 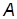 (ось абсцисс) и
(ось абсцисс) и 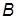 (ось ординат); оцифровку осей задать в пределах от 0 до 6;
(ось ординат); оцифровку осей задать в пределах от 0 до 6;
· изобразить границу устойчивости согласно уравнению 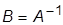 (выше этой границы располагается область устойчивости);
(выше этой границы располагается область устойчивости);
· для значений 0 < A £ 3 изобразить кривую DC, описываемую уравнением 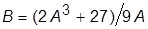 ; правая граница этой кривой – точка C имеет координаты (3;3);
; правая граница этой кривой – точка C имеет координаты (3;3);
· изобразить кривые CE и CF (симметричные относительно биссектрисы квадранта), которые описываются одним и тем же параметрически заданным уравнением 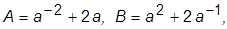 где
где 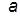 – параметр; для построения кривой CE необходимо задавать
– параметр; для построения кривой CE необходимо задавать 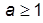 (здесь
(здесь 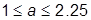 ), а для построения кривой CF – 0 < a £ 1 (здесь
), а для построения кривой CF – 0 < a £ 1 (здесь 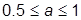 );
);
· обозначить цифрами I, II, и III следующие области:
I – между границей устойчивости и линией DCF (в этой области ХП имеет один вещественный корень и пару комплексно-сопряженных корней, расположенных ближе к мнимой оси, чем вещественный);
II – выше кривой DCE (здесь ХП имеет те же типы корней, что и в области I, но ближайшим к мнимой оси является вещественный корень);
III – между кривыми CF и CE (здесь все корни ХП вещественны).
2.4. Контрольные вопросы
1. Дайте определения основных показателей качества динамики САУ.
2. Как уменьшение запаса устойчивости отражается на значениях других показателей качества ?
3. Какими мерами можно повысить критическое значение контурного коэффициента усиления системы?
4. В чем польза диаграммы Вышнеградского?
5. Почему граница устойчивости на диаграмме описывается уравнением 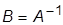 ?
?
6. Каковы значения корней ХП в точке C ?
Лабораторная работа № 3
Основные сведения
Синтез САУ, удовлетворяющей заданным требованиям к точности системы и качеству ее динамики, обычно проводят в два этапа:
1-й этап – проектирование основного регулятора, обеспечивающего заданную точность;
2-й этап – синтез специальных корректирующих устройств (КУ) для стабилизации системы, если она неустойчива, и(или) улучшения ее динамических свойств.
Среди КУ различают последовательные, включаемые в прямой канал системы, и параллельные, представляющие собой, как правило, различного рода обратные связи, чаще местные, т. е. охватывающие часть звеньев прямого канала. Достоинством таких КУ по сравнению с последовательными является то, что при правильном расчете (таком, чтобы в существенном диапазоне частот ЧПФ разомкнутого внутреннего контура была значительно больше единицы) ПФ внутреннего контура определяется в основном ПФ корректирующей обратной связи, вследствие чего вариации параметров звеньев, охваченных обратной связью, слабо влияют на динамику системы. Применяют также КУ, включаемые параллельно звеньям прямого канала.
Синтез САУ в частотной области обычно состоит в формировании желаемой ЛАХ разомкнутой системы с последующим расчетом корректирующего устройства, чаще параллельного, введение которого обеспечит эту ЛАХ. Однако в случае последовательной коррекции часто можно обойтись более простой процедурой введения в систему типовых КУ. Объединяя одним понятием "регулятор в прямом канале" основной регулятор и последовательное КУ, можно указать следующие типовые регуляторы, широко применяемые для улучшения динамики и повышения точности систем:
· П-регулятор: 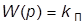 (при
(при 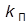 > 1 увеличивает
> 1 увеличивает 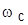 и уменьшает
и уменьшает 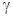 );
);
· И-регулятор: 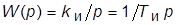 (повышает порядок астатизма и уменьшает
(повышает порядок астатизма и уменьшает 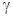 на
на 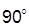 );
);
· ПД-регулятор (форсирующее звено): 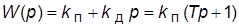 (повышает
(повышает 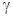 ; реализуемая ПФ
; реализуемая ПФ 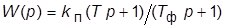 , где
, где 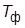 <<
<< 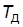 );
);
· ПИ-регулятор: 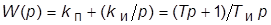 (обладает свойствами П-регулятора и первым из свойств И-регулятора);
(обладает свойствами П-регулятора и первым из свойств И-регулятора);
· ПИД-регулятор: 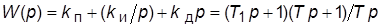 (сочетает свойства ПИ- и ПД-регуляторов; реально
(сочетает свойства ПИ- и ПД-регуляторов; реально 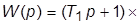
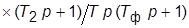 , где
, где 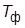 – малая постоянная времени).
– малая постоянная времени).
Некоторые способы определения порядка астатизма 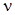 системы в отношении воздействия
системы в отношении воздействия 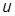 :
:
· представить ПФ для ошибки 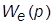 = E(p)/U(p)в виде
= E(p)/U(p)в виде 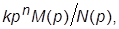 где M(p) и N(p) – полиномы, причем
где M(p) и N(p) – полиномы, причем 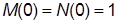 ; тогда
; тогда 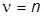 ;
;
· определить порядок астатизма как максимальное число не охваченных местными обратными связями интегрирующих звеньев в обратной связи системы с входом u и выходом e (ошибкой).
Программа работы
1. Задать структурную схему (рис. 3.1, где y – регулируемая переменная; g и f – задающее и возмущающее воздействия; e – ошибка). Назначить произвольное значение T из диапазона 0.1…1.0 с.
2. Получить ПХ по задающему воздействию 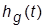 и определить
и определить 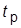 и
и 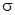 для ряда возрастающих значений k:
для ряда возрастающих значений k: 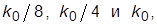 где
где 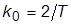 – номинальное значение k. Описать, как с ростом
– номинальное значение k. Описать, как с ростом  изменяются характер переходного процесса и значения показателей качества ПХ.
изменяются характер переходного процесса и значения показателей качества ПХ.
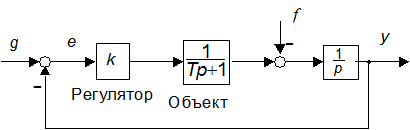
Рис. 3.1
3. Получить ПХ по возмущающему воздействию 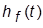 (g = 0, f = 1) и определить
(g = 0, f = 1) и определить 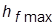 и
и 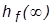 , задав
, задав 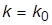 . Найти установившуюся ошибку
. Найти установившуюся ошибку 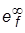 на входе регулятора от возмущения f = 1. Убедиться, что ½
на входе регулятора от возмущения f = 1. Убедиться, что ½ 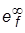 ½=½
½=½ 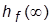 ½.
½.
4. Задать новую ПФ регулятора вида 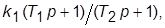 приняв
приняв 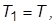
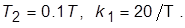 Оценить количественно изменение значений
Оценить количественно изменение значений 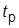 ,
, 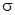 ,
, 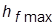 и
и 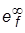 . Пояснить результаты для
. Пояснить результаты для 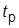 и
и 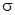 , записав ПФ и построив асимптотические ЛАХ разомкнутой системы для обоих регуляторов.
, записав ПФ и построив асимптотические ЛАХ разомкнутой системы для обоих регуляторов.
5. Сохранив численные значения параметров схемы, дополнить ее, включив в прямой канал последовательно еще одно КУ с ПФ 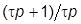 , задав значение
, задав значение 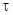 не менее (10…20)
не менее (10…20) 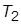 . Изменилась ли ПХ по задающему воздействию? Что произошло с ошибкой
. Изменилась ли ПХ по задающему воздействию? Что произошло с ошибкой 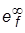 ? Изменился ли порядок астатизма по возмущению?
? Изменился ли порядок астатизма по возмущению?
6. Задать схему (рис. 3.2) при 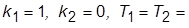
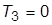 (исходная система). Получить ПХ и сделать суждение об устойчивости исходной системы. Стабилизировать систему уменьшением
(исходная система). Получить ПХ и сделать суждение об устойчивости исходной системы. Стабилизировать систему уменьшением 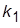 . Измерить
. Измерить 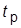 и
и 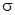 . Определить приблизительное критическое значение
. Определить приблизительное критическое значение 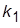 .
.
7. Восстановить 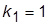 . Вводя по отдельности корректирующие связи с передачами
. Вводя по отдельности корректирующие связи с передачами 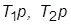 и
и 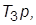 добиться стабилизации системы. Определить приемлемые с точки зрения качества ПХ значения
добиться стабилизации системы. Определить приемлемые с точки зрения качества ПХ значения 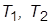 и
и 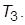 Для каждой связи сделать эскиз ПХ и измерить
Для каждой связи сделать эскиз ПХ и измерить 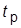 и
и 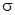 .
.
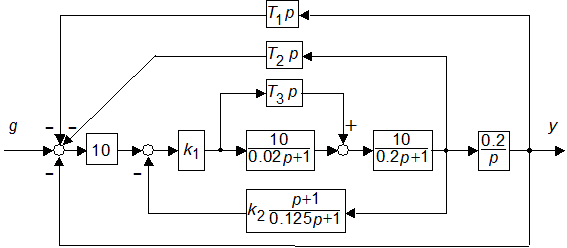
Рис. 3.2
8. Задать 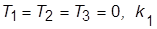 из диапазона 32…50,
из диапазона 32…50, 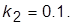 Получить ПХ, сделать ее эскиз или копию экрана и зафиксировать
Получить ПХ, сделать ее эскиз или копию экрана и зафиксировать 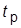 и
и 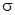 .
.
Содержание отчета
1. Структурные схемы и численные значения их параметров.
2. Результаты по каждому пункту программы работы и комментарии к ним. Ответы на вопросы, содержащиеся в программе.
3. Указание типа использованного регулятора (П-, ПИ- и т. п.).
4. Асимптотические ЛАХ первой системы, согласно пп. 4 и 5 программы.
5. Асимптотические ЛАХ второй системы: исходной и скорректированной введением связей с передачами 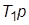 и
и 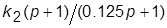 (все ЛАХ – для разомкнутой системы). В последнем случае использовать правило приближенного построения результирующей ЛАХ соединения с обратной связью.
(все ЛАХ – для разомкнутой системы). В последнем случае использовать правило приближенного построения результирующей ЛАХ соединения с обратной связью.
Контрольные вопросы
1. Как выглядят ЛЧХ ПД-, ПИ-, и ПИД-регуляторов ?
2. Как определить порядок астатизма системы по заданному воздействию?
3. Почему ПД-регулятор повышает запас устойчивости, а ПИ-регулятор – порядок астатизма?
4. Как наклон ЛАХ разомкнутой системы на частоте среза и в ее окрестности влияет на динамические свойства системы?
5. Как называются корректирующие устройства на рис. 3.2?
Лабораторная работа №4
Основные сведения
Системы подчиненного регулирования (СПР) построены по каскадному принципу, т. е. с вложенными друг в друга (подчиненными) контурами. Выходная величина регулятора i-го контура служит задающим воздействием для (i –1)-го контура. Каждый контур содержит регулятор с ПФ 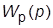 , звенья с малыми постоянными времени
, звенья с малыми постоянными времени
