Функции нескольких действительных переменных

Переменная величина z называется функцией двух переменных величин х и у, если каждой паре допустимых значений х и у соответствует единственное значение z. Функции двух переменных обозначают символами z=f(x, у), z = F(x,y), z = z(x, у) и т. п. Значение функции z=f(x, у) при х = а и у = b обозначают через f(a, b). Упорядоченная пара значений х и у называется точкой М(х; у), а функция двух переменных — функцией этой точки z=f(M). Переменная величина u называется функцией трех переменных величин х, у, z, если каждой упорядоченной тройке значений х, у, z соответствует единственное значение u. Аналогично определяется функция n переменных.

Множество всех точек, в которых определена функция n переменных, называется областью определения (существования) функции. Некоторую замкнутую область D на плоскости, ограниченную данными линиями, можно задать с помощью одной или нескольких систем неравенств вида

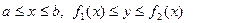(1)

Число А называется пределом функции z=z(x,y)=z(P) в точке 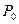( 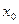; 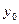),если для любого числа 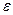>0 существует такое число б>0, что для всех точек P(x;y), лежащих внутри круга с центром в точке P₀ и радиусом б (кроме,быть может,самой точки P₀), выполняется неравенство .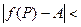

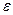Коротко это записывается так же:

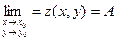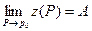или (2)

Отметим, что этот предел не должен зависеть от способа приближения точки P к точке P₀, т.е. точка P стремится к точке P₀ по любой траектории.

Для функции двух переменных имеют место теоремы о пределе суммы, разности, произведения и частного, аналогичные соответствующим теоремам для функции одного аргумента.

Функция z=z(x,y)=z(P) называется непрерывной в точке P₀(x₀;y₀) если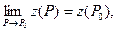

т.е. если предельное значение функции в точке равно ее частному значению в этой точке.

Функция, непрерывная в каждой точке какой-либо области, называется непрерывной в этой области.

Точка P₀ называется точкой разрыва функции z=z(P), если эта функция определена в некоторой окрестности точки P₀ и в ней непрерывность функции нарушается.

Функция z=z(P) может иметь разрывы не только в изолированных точках, но так же и на множестве точке, например на линиях разрыва.

Сумма, разность, произведение и частное непрерывных функций двух аргументов в некоторой точке так же являются непрерывными функциями в этой точке. Аналогично определяются понятия предела и непрерывности для функций трех и большего числа переменных.

Пример по выполнению практической работы

Пример 1. Найти область определения функции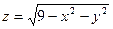

Решение: Данная функция определена, если 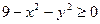, т.е. 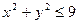. Этому соотношению удовлетворяют координаты всех точек плоскости, которые находятся внутри круга радиуса R = 3 с центром в начале координат, а также на его границе. Областью определения данной функции и является указанный круг.

Пример 2. Найти область опре­деления функции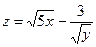

Решение:Первое слагаемое определено при x ≥ 0, второе - при у > 0. Следовательно, область определения есть I-ая четверть плоскости хОу.

Пример 3. Дана функция 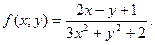Вычислить .

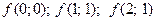Решение:

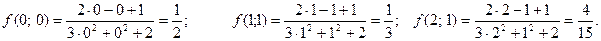
Пример 4. Найти пределы: 1) 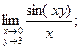2)

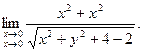
Решение. 1) Так как 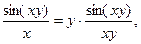то .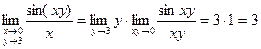

2) Здесь требуется вычислить предел при условии 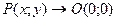, т.е. при условии 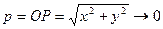. Находим:

.

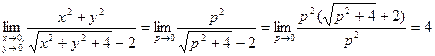Задания для практического занятия:

Вариант 1

1) Найти область определения функции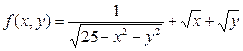

2) Вычислить значение функции f(1;2), если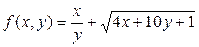

Вариант 2

1) Найти область определения функции ;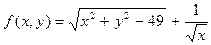

2) Вычислить значение функции f(-2;3), если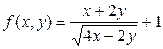

Вариант 3

1) Найти область определения функции ;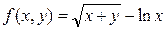

2) Вычислить значение функции f(5;-3), если ;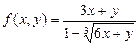

Вариант 4

1) Найти область определения функции ;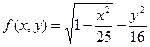

2) Вычислить значение функции f(-2;6), если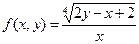

Контрольные вопросы

1.Дать определение функции двух действительных переменных;

2. Что представляет собой область определения функции двух действительных переменных?

3.Дать определение предела функции двух действительных переменных.

Практическая работа №21