Teма 4.5. Местные гидравлические сопротивления.

Основные виды местных сопротивлений. Коэффициент местных по­терь. Местные потери при больших числах Рейнольдса. Внезапное и пос­тепенное изменение сечение трубопровода. Теорема Борца. Потери на­пора в диффузорах и конузорах. Повороты трубопроводов. Сопротивления с переменной формой, прочной части. Определение суммарных потерь. Эквивалентные длины труб. Взаимное влияние местных сопротивлений.

Указания к теме 4.5.

1. Местными сопротивлениями называют короткие участки трубопроводов, на которых происходят изменения вели­чины или направления скоростей потока из-за изменения конфигурации твердых границ.

Потери энергии в местных сопротивлениях, отнесен­ные к единице веса потока жидкости, называются мест­ными потерями напора и подсчитываются по общей фор­муле

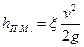(4.5.1)

где 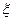— безразмерный коэффициент местного сопротив­ления;

v — средняя скорость потока (обычно — в сечении трубопровода перед местным сопротивлением или после него).

Значение 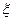вообще зависит от формы местного сопро­тивления, шероховатости его стенок, условий входа и выхода из него жидкости и основного критерия динами­ческого подобия напорных потоков — числа Рейнольдса.

Число Рейнольдса обычно относят к сечению трубо­провода, на котором находится местное сопротивление:

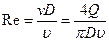
где 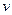и Q — средняя скорость потока и расход в трубе; D — диаметр трубы; 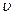— кинематическая вязкость жидкости.

Для большинства местных сопротивлений в трубопро­водах при числах Рейнольдса 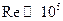имеет место тур­булентная автомодельность — потери напора пропорцио­нальны скорости во второй степени и коэффициент сопро­тивления не зависит от Re (квадратичная зона сопротив­ления).

В тех местных сопротивлениях, где основной является вихревая потеря напора (например, резкое изменение сечения трубопровода, диафрагмы и др.), автомодельность устанавливается при значительно меньших числах Рейнольдса ( ) .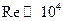

В случае внезапного расширения трубопровода мест­ная потеря напора при больших числах Рейнольдса вы­ражается формулой

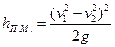, (4.5.2)

в соответствии с которой коэффициент местного сопротив­ления, отнесенный к скорости v₁.

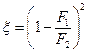(4.5.3)

В формулах (2) и (3) и v₂ — средние скоро­сти в узком (входном) и широком (выходном) сечениях потока;F₁ и F₂ — площади этих сечений.

При постепенном расширении потока в диффузоре:

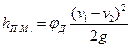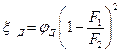; , (4.5.4)

где 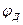— безразмерный коэффициент потерь, выражающий потерю в диффузоре в долях от потери при внезапном расширении.

При внезапном сужении трубопровода местная потеря напора:

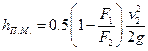, (4.5.5)

где F₁ и F₂ — площади широкого (входного) иузкого (выходного) сечений; v₂ — выходная скорость.

Значение коэффициента сопротивления входа в трубу из большого резервуара зависит от формы входной кромки. В случае острой входной кромки при больших числах Рейнольдса можно принимать .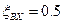

При выходе потока из трубы в резервуар потеря напора и коэффициент сопротивления выхода равны:

; ,

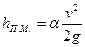где v — средняя скорость в выходном сечении трубы; 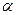— коэффициент кинетической энергии (при турбулент­ном режиме 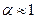и ).

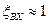При последовательном расположении в трубопроводе различных местных сопротивлений общая потеря напора определяется как сумма потерь в отдельных сопротивле­ниях, вычисляемых по указанным выше значениям .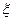

если между этими местными сопротивлениями имеются участки трубопровода длиной не менее пяти-шести диа­метров. На этих участках поток, вышедший из одного местного сопротивления, стабилизируется до входа в сле­дующее сопротивление. При более близком расположе­нии местных сопротивлений необходимо учитывать их взаимное влияние.

В приводимых ниже зада­чах предполагается, что мест­ные сопротивления доста­точно удалены друг от друга и их взаимное влияние от­сутствует.

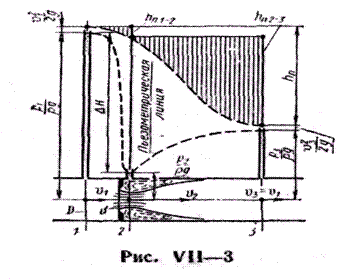
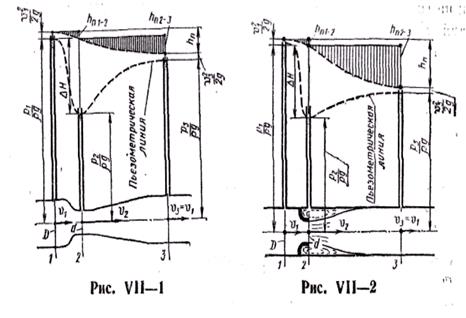
1.Для расходомеров, основанных на создании пе­репада давлений в потоке различными сужающими устройствами (труба Вентури, сопло и диафрагма — см. рис. VII—1, VII—2 и VII—3), расход определяется по общей формуле:

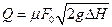, (4.5.6)

где 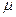— коэффициент расхода; 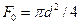— наимень­шая проходная площадь расходомера; 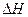— падение гидростатического напора (пьезометрического уровня) на участке между входным и суженным сечениями потока в расходомере.

Величина 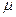определяется опытным путем и зависит от конструктивных форм расходомера, отношения площа­дей 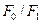( 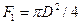— проходная площадь трубопро­вода) и расположения мерных точек, а также от числа Рейнольдса 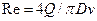. Зона турбулентной автомодельности по коэффициенту расхода для этих расходоме­ров имеет место в зависимости от 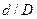при .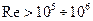

Потери напора в расходомерах вычисляют по общему выражению (1), где v — средняя скорость в трубопро­воде и 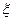— суммарный коэффициент сопротивления рас­ходомера, также определяемый опытным путем.

Значения коэффициента расхода 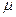и коэффициента сопротивления 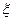, расходомеров в зоне турбулентной автомодельности можно приближенно определить и расчет­ным путем. В качестве примера получим общие выра­жения 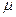и 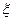для диафрагмы (рис. VII—3).

Для коэффициента расхода можно воспользоваться формулой(14) гл. VI, определяющей расход при исте­чении через отверстие из резервуара ограниченной пло­щади; непосредственно получаем:

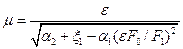, (4.7)

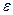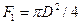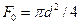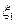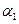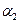где — коэффициент сжатия струи, зависящий от соот­ношения площадей трубы и отверстия диаф­рагмы ; — коэффициент сопротивления от­верстия диафрагмы; и — коэффициенты кинетиче­ской энергии в сечении 1перед входом в диафрагму и в сжатом сечении струи 2 (для больших значений Re можно принимать ).

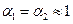При 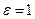формула дает выражение коэффициента расхода трубы Вентури и сопла (рис. VII —1 и VII—2).

Приближенность формулы для и. обусловлена неточ­ностями расчетных значений входящих в нее коэффициен­тов, а также тем, что давления у сужающего устройства часто измеряют не в расчетных сечениях потока (1 и 2), а в углах, образуемых сужающим устройством со стенками трубы (угловой отбор давлений в нормальных расходомерах).

Коэффициент сопротивления можно найти расчетом, рассматривая потерю напора в диафрагме как сумму потерь на участках между сечениями 1—2 и 2—3;

.

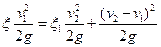Применяя уравнение расхода : 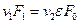,откуда .

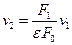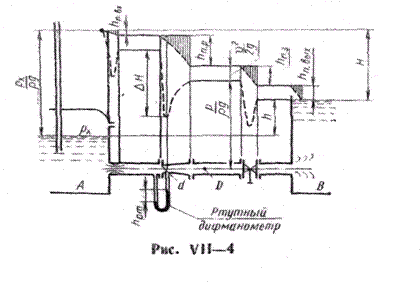
получаем:

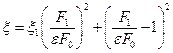(4.5.8)

При 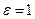это выражение дает коэффициент сопротивления мерного сопла. Для трубы Вентури в резуль­тате аналогичного расчета получим (см. также введе­ние к гл. VI).

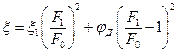(4.5.9)

3. Рассмотрим в качестве примера расчета схему тру­бопровода с местными сопротивлениями, в которой жид­кость плотностью р перетекает по трубопроводу диаме­тром D из бака А в бак В с постоянной разностью уров­ней h под избыточным давлением р_х в баке А (рис. VII—4).

На трубопроводе установлены расходомер Вентури с диаметром узкого сечения d и задвижка.

Заданы (в предположении, что имеет место квадратич­ная зона сопротивления ибезразмерные характеристики потока не зависят от числа Рейнольдса) коэффициент расхода 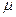и коэффициент сопротивления 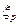расходомера Вентури, а также коэффициент сопротивления 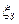задвижки.

Определим расход Q в трубопроводе и давление р_х в баке А, считая известным показание h_pт ртутного диф­ференциального манометра, присоединенного к трубе Вентури.

Расход в трубопроводе по показанию дифференциаль­ного манометра на трубе Вентури равен согласно фор­муле (6):

,

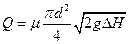где перепад пьезометрических уровней (в горизонтальной трубе — перепад давлений, выраженный, в метрах столба протекающей жидкости)

.

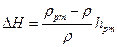Для определения давления р_х воспользуемся уравне­нием Бернулли, записанным для сечений потока на сво­бодных поверхностях в баках:

,

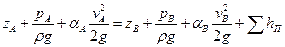где 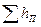— сумма потерь напора между этими сечениями. Так как скоростные напоры в баках пренебрежимо малы ( 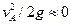и 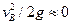), получаем общее соотно­шение:

,

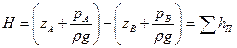выражающее, что разность Н гидростатических напоров (пьезометрических уровней) в баках целиком затрачи­вается на преодоление гидравлических сопротивлений, возникающих при перетекании жидкостипо трубопро­воду.

В рассматриваемом случае 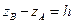и избыточное давление 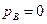, Следовательно, .

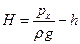Пренебрегая потерями трения по длине трубопровода (который предполагается коротким), определим местные потери — на входе в трубопровод: 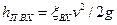, в рас­ходомере Вентури: 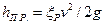, в задвижке: 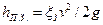,на выходе из трубопровода: 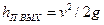, гдесредняя скорость в трубопроводе

.

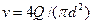Таким образом, искомое давление можно определить из формулы:

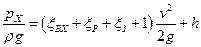
4. В ряде случаев (для труб малых диаметров и жидко­стей большой вязкости) оказывается практически важным учет влияния числа Рейнольдса на коэффициенты мест­ных сопротивлений. При очень малых значениях Re (примерно 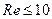) существует зона ламинарной автомодельности, в которой местные потерн напора пропор­циональны скорости потока и коэффициент местного сопро­тивления выражается формулой

,

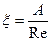где множитель пропорциональности А определяется фор­мой местного сопротивления.

Большим значениям числа Рейнольдса ( 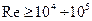) отвечает зона турбулентной автомодельности, в ко­торой закон сопротивления является квадратичным и 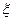= const.

Переход от первой автомодельной зоны ко второй имеет сложный характер и индивидуальные особенности в мест­ных сопротивлениях различного типа.

Для большинства местных сопротивлений оценку ве­личины 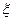в переходной зоне можно сделать по формуле А. Д. Альтшуля:

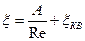,(4.5.10)

где 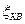— значение коэффициента местного сопротивления в квадратичной зоне.

Вопросы для самопроверки.

1. Какие сопротивления называются местными?

2. По какой формуле определяются потери напора в местных сопротивлениях?

3. В чем заключается физический смысл коэффициента местного сопротивления и от чего он зависит?

4. В каком сечении берется скорость при определении местных потерь напора?

5 .Каковы возможные пути снижения потерь в диффузорах с большим углом расширения?

6. В чем состоит принцип наложения потерь?

7. Как определяется суммарный коэффициент сопротивления?