Оптимальный рост: формулы критерия Келли для практиков

Поскольку критерий Келли асимптотически максимизирует ожидаемую норму роста капитала, он часто называется стратегией оптимального роста. Интересно сравнить его с другими стратегиями фиксированных долей. Я представлю некоторые результаты, которые нахожу полезными для практики. Я хочу постараться объяснить все это просто и понятно. Эти результаты появились после размышлений об "интересных вопросах". Я не делал полную литературную выборку, но я знаю, что похожие результаты были уже представлены математической общественности. См. например. Browne (1995, 1996) и дальнейшие ссылки.

(a) Вероятность достижения установленной цели за n попыток.

Сначала рассмотрим подбрасывание монеты. Мы начнем с изложения связанных с нашей задачей особенностей стандартного Броуновского движения. Howard Tucker обратил на них мое внимание еще в 1974 году, и это, вероятно, наиболее полезный отдельный факт из всех, что я знаю, имея дело с разнообразными проблемами азартных игр и с теорией производных финансовых инструментов. Для стандартного Броуновского движения X (t) мы имеем

где α=а√Т, а β =b/√T. См. Рисунок 2 и Приложение 2, где дан вывод формулы (3.1)

В нашем случае а < 0, b > 0, так что lim_T→∞ P(X(t) ≥ at + b, 0 ≤ t ≤ T)=1.

Пусть f будет долей ставки. Пусть Y_i , i=1..., n,– независимые тождественно распределенные (i.d.d..) величины. P (Y_i=1)=p > 1/2, P (Y_i =-1)=q < 1/2; пусть также p < 1, во избежание тривиального случая p= 1.

Ставим фиксированную долю ставки f, 0 < f < 1, в каждой попытке. Пусть V_k будет величина капитала игрока или инвестора через k попыток, при начальном значении V₀. Выберем Vo= 1 (без потери общности); число попыток n; цель С > 1.

Какова вероятность того, что V_k ≥ С для некоторого k, 1 ≤ k ≤ n? Она та же самая, как вероятность, что log V_k; ≥ log C для некоторого k, 1 ≤ k ≤ n. Обозначая ln=log_e, имеем:

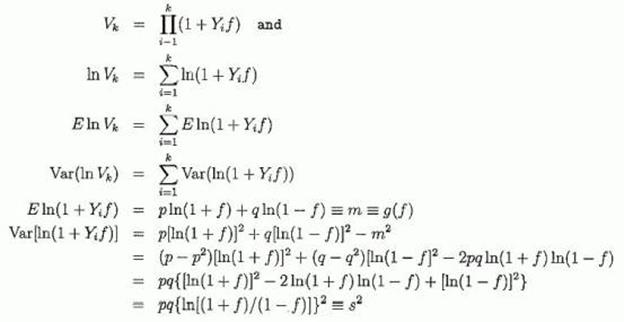
Сдвиг за n попыток: nm

тогда и только тогда, когда:

Дисперсия за n попыток: s²n

где

, или, равносильно:

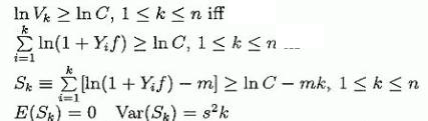
Мы хотим найти вероятность Рrob(S_k ≥ ln C - mk, 1 ≤ k ≤ n).

Для этого мы используем нашу формулу Броуновского движения, чтобы аппроксимировать S_n через Prob (X(t) ≥ lnС - Хt/s², 1 ≤ t ≤ s²n) где каждое значение S_n приближено равно X(t) со сдвигом 0 и дисперсией s² (0 ≤ t ≤ s², s² ≤ t ≤ 2s²..., (n - 1)s² ≤ t ≤ ns²). Замечание: приближение "хорошо" только для "больших" n.

Тогда в формуле (3.1):

Пример 3.1

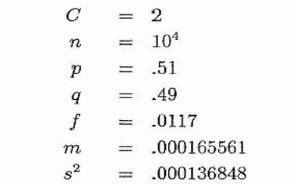
Откуда P(·)=0.9142

Пример 3.2

Повторим решение Примера 3.1 при

f =0.02;

тогда m=0.000200013

s² =0.000399947,

и P(∙)=0.9214

(b) Вероятность того, что капитал когда-либо уменьшится до доли x от начальной величины

Это вопрос, который причиняет много волнений игрокам и инвесторам. На него легко можно ответить, хотя бы и приблизительно, используя наши предыдущие методы.

Используя обозначения предыдущего раздела, мы хотим найти P (V_k ≤ x для некоторых k, 1 ≤ k ≤ ∞). Сходные с этими методы выдают (намного проще) формулу непрерывного приближения:

Prob (·)=e^2ab, где a =- m/s², а b=- ln x, что можно записать, как

(3.2) Prob (·)= x^(2m/s²) , где ^ означает возведение в степень.

Пример 3.3.

p=0.51 f=f* =0.02

2m/s²=1.0002

Prob(·) =x

Мы увидим в разделе 7, что для ограниченного непрерывного приближения и оптимальной доли Келли f*, Р (V_k (f *) ≤ x для некоторых k ≥ 1)=x.

Мой опыт показывает, что большинство осторожных игроков или инвесторов, которые используют Келли, находят частоту существенного сокращения капитала неудобно большой. Теперь мы видим почему. Чтобы уменьшить ее, они предпочитают ставить несколько меньше, чем рекомендуемая доля ставки f*. Это также повышает уровень безопасности в случае, если игровые ситуации менее благоприятны, чем ожидалось. Потери из-за уменьшенном роста капитала не является серьезными для умеренной «недоставки». Мы обсудим это позже, в разделе 7.

(с) Вероятность попадания в или выше указанной величины
в конце определенного числа попыток.

Доктор Richard Hecht (1995) предложил взять эту вероятность в качестве цели и использовал для этого численный метод определения оптимальной (в соответствии с этим критерием) фиксированной доли для p - q= 0.02 и различных с, n и определенных вероятностей успеха.

Это - намного более легкая задача, чем похожая на нее (a). Для вероятности того, что X(T) в конце концов превысит цель, мы получаем:

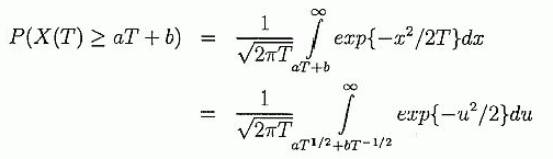
где и=x/√Tтак что x=aT +b дает u√T =aT + b иU=aT^1/2-bT^-1/2. Интеграл равен

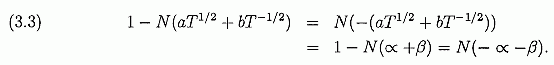
Для Примера (3.1): f =0.0117 и P=0 .7947. Для Примера (3.2): P=0.7433. Пример (3.1) - для оптимальной доли Хечта, а Пример (3.2) - для оптимальной доли Кэлли, Обратите внимание на различие значений P.

Наши числовые результаты соответствуют моделированию Хечта в проверенных нами случаях.

Браун (1996) дал изящное решение проблемы в непрерывном приближении: какая стратегия максимизирует вероятность достижения установленной цели С к или до указанного времени n и какова соответствующая вероятность успеха? Обратите внимание, что, в общем случае, оптимальная стратегия будет включать механизм изменения доли ставки в зависимости от оставшегося времени и расстояния до цели.

Рассмотрим пример предельного случая, когда n=1 , а C=2. Если X₀<1, то никакая стратегия не сработает и вероятность успеха равна 0. Но, если 1 ≤ X₀ ≤ 2, нужно делать ставку по крайней мере 2 - X₀, таким образом любую долю f ≥ (2 — X₀)/X₀, для вероятности успеха p. В другом предельном случае: n=10, С= 2¹⁰ =1024, X₀=1. Здесь единственная стратегия, которая может преуспеть, состоит в том, чтобы делать ставку f=1 в каждой попытке. Вероятность успеха равна p¹⁰ для этой стратегии и 0 для всех других (если p < 1), включая Келли.

(d) Непрерывная аппроксимация времени, ожидаемого для достижения цели.

Согласно Теореме l (v), стратегия оптимального роста асимптотически минимизирует ожидаемое время достижения цели. Вот что это означает. Предположим для цели С, что m(C) – наибольшее значение нижней границы для ожидаемого времени достижения C из всех стратегий. Предположим, t*(C) - ожидаемое время при использовании стратегии Келли. Тогда lim_C→∞ (t*(c)/m(c))= 1.

Непрерывное приближение к ожидаемому числу попыток для достижения цели C>X₀=1 будет

(3.4) n(C,f)=(lnC)/g(f)

где f - любая стратегия фиксированной доли. В Приложении 3 дан вывод этих формул. Теперь, т.к. g(f) имеет единственный максимум g(f*), то и n(C, f) имеет единственный минимум на f=f*. Кроме того, мы можем увидеть, насколько дольше, в среднем, придется добираться до С при отклонении от f*.

(e) Сравнение стратегий с фиксированной долей: вероятность, что одна стратегия опередит другую после n попыток.

Теорема 1 (iv) гласит, что капитал при использовании стратегии Келли будет стремиться, в конечном счете, к бесконечно большому приумножению капитала, чем использовании любой "существенно иной" стратегии. Можно показать, что любое фиксированное f ≠ f* - это "существенно иная" стратегия. Это приводит нас к вопросу о том, насколько стратегия Келли опережает другую стратегии фиксированной доли, и шире говоря, насколько быстро одна стратегия фиксированной доли опережает другую (или отстает от другой).

Если W_n - число побед за n попыток, а n — W_n - число проигрышей, то

G(f)=(W_n/n) ln (l + f) + (1 - W_n/n) ln (1 - f)

это фактически (случайная переменная) коэффициент роста.

Как мы видели, его ожидание

(3.5) g(f)=E(G(f))=p log(1 + f) + qlog(1 - f)

а дисперсия G(f) -

и из этого следует, что G(f), который представиться как G(f)=a(∑T_k)/n+b, приблизительно нормально распределено со средней g(f) и дисперсией VarG(f). Это позволяет нам получить распределение X_n и еще раз ответить на вопрос заданный в 3(c). Проиллюстрируем это на примере.

Пример 3.3 p=0.51 q=0.49 f*=0.02 N=10,000 и

s= стандартное отклонение G(f)

Далее находим распределение G(f₂) - G(f₁). Мы рассматриваем два случая.

Случай 1. Одна и та же игра.

Здесь мы предполагаем, что оба игрока делают ставки на одни и те же попытки, например, на монету, или на одинаковые сдачи в блэк джеке, или на одно и тот же исход на тотализаторе. На рынке акций, оба игрока могут вкладывать в одну и ту же бумагу одновременно, например, инвестирую в индексный фонд S&P 500.

Мы находим

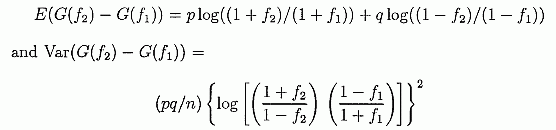
где G(f₂) — G(f₁) приблизительно нормально распределено с этими средним и дисперсией.