Случайные величины и их классификация.

В различных физических явлениях и производственных процессах некоторые величины изменяются, а другие сохраняют свое числовое значение. Например, при работе токарного станка время, расстояние перемещения суппорта изменяются (переменные величины обычно обозначаются x, y, z), а скорость вращения детали остаётся условно-постоянной (будем такие величины обозначать – a, b, c). Но, как известно, абсолютных констант в природе очень мало. Наблюдаемые в технике параметры производственных процессов и характеристики качества, относящиеся как к названным выше переменным, так и к условно-постоянным величинам, являются случайными величинами.

Случайной величиной называется величина, которая в результате испытаний или контроля может принять то или иное значение в границах определенного интервала.

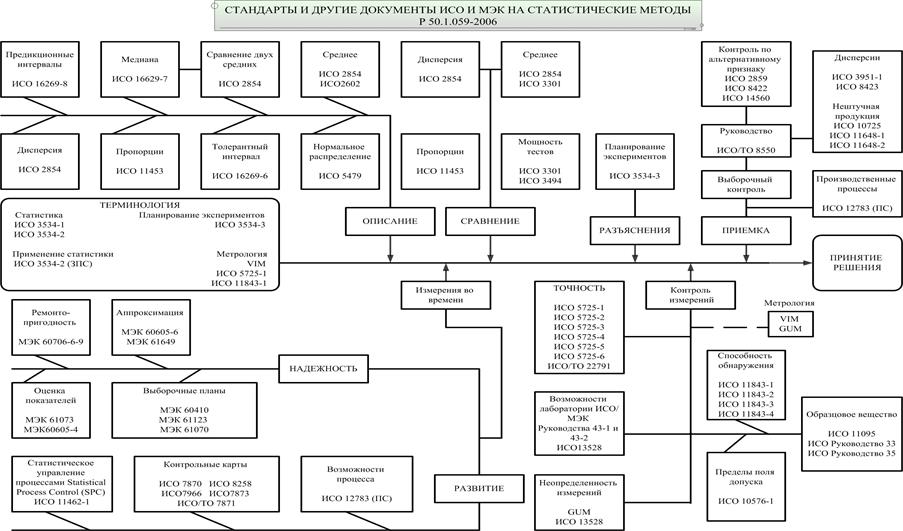
Рис. 1.1. Руководство по выбору статистических методов для стандартов и технических условий (Р 50.1.059-2006).

Например, действительный размер обработанной детали является случайной величиной, так как он может принять любое численное значение в определенных пределах. По роли в исследовании они классифицируются на зависимые и независимые (рис. 1.2).

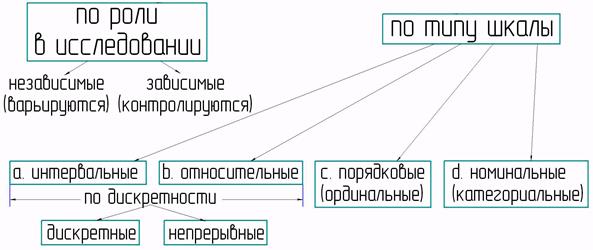
Рис. 1.2 Классификация случайных величин

Независимыми случайными величинами (факторами, также «объясняющими», «экзогенными» случайными величинами или «предикторами», x_i) называются случайные величины, которые варьируются исследователем.

Примераминезависимых случайных величин могут быть:

- скорость вращения шпинделя,

- подача суппорта станка,

- используемая смазочно-охлаждающая жидкость,

- марка материала, конструкция или иная характеристика инструмента и т. д.

Независимые случайные величины зависят только от экспериментатора, который манипулирует ими, воздействуя на "зависимые случайные величины".

Зависимые случайные величины(называемые также «эндогенными» или «откликами», y_i) измеряются или регистрируются и являются обычно предметом оптимизации

В качестве последних могут быть производительность, характеристики качества, экономические показатели и т.д. Иначе, зависимость проявляется в ответной реакции исследуемого объекта на воздействие.

Типы случайных величин. В зависимости от используемой шкалы измерений, как правило, случайные величины разделяют на четыре основные типа (см. рис. 1.2):

а. Номинальные (категориальные) случайные величины используются только для качественной классификации. Типичные примеры номинальных случайных величин - пол, национальность, цвет, название страны или города и т.д. Применительно к металлообработке это могут быть виды брака или разделение продукции на «годную» и «негодную».

b. Порядковые (ординальные) случайные величины позволяют ранжировать (упорядочить) объекты, указав какие из них в большей или меньшей степени обладают качеством, выраженным данной случайной величиной. Однако они не позволяют сказать "на сколько больше" или "на сколько меньше". Например, можно случайную величину, выражающую возраст (мальчик - юноша - мужчина - старик), оценивать в баллах. Таким же образом в баллах можно оценивать знания студентов, качество детали, пригодность технологического процесса.

c. Интервальные случайные величины позволяют не только упорядочивать объекты измерения, но и численно выразить и сравнить различия между ними. Например, температура, измеренная в градусах Фаренгейта или Цельсия, размер детали, шероховатость её поверхности характеризуются «в интервальной шкале». Можно, например, сказать, что температура 40^ОС выше, чем температура 30^ОС на 10 градусов.

d. Относительные случайные величины очень похожи на интервальные случайные величины. В дополнение ко всем свойствам случайных величин, измеренных в интервальной шкале, их характерной чертой является наличие определенной точки абсолютного нуля. Примером относительной случайной величины является температура, выраженная по шкале Кельвина. Применительно к этих случайным величинам можно оценивать во сколько раз одна величина больше или меньше другой. То есть допустимо выражение типа: 40^ОК в два раза больше, чем 20^ОК. Интервальные шкалы, например, шкала Цельсия данным свойством не обладают. Следует заметить, что в большинстве статистических процедур не делается различия между свойствами интервальных шкал и шкал отношения.

Интервальные и относительные случайные величины могут быть дискретными и непрерывными(см. рис. 1.2).

Дискретной случайной величиной называется такая величина, которые при­нимают отдельные, большей частью целочисленные значения.

Непрерывной случайной величиной называется такая величина, которая может принимать любые численные значения из интервала возможных значений.

Напри­мер, число деталей, обработанных на станке, есть дискретная случайная величина, а размер детали - непрерывная случайная величина. (Иногда используется понятие «смешанной случайной величины», которая определяется наличием нескольких непрерывных интервалов возможных значений, разделённых промежутками).

По временной принадлежности случайные величины обычно делятся на два вида: перекрёстные данные (cross-section data) и временные ряды (time series).

Перекрёстные данные- определяют значения показателей, относящихся к одному моменту времени, либо значения показателей, временная принадлежность которых несущественна. Например, при исследовании зависимости шероховатости поверхности от состава СОЖ, если сравниваются средние значения шероховатости деталей, обработанных в различных СОЖ, время и порядок обработки деталей неважны.

Временной ряд, ряд динамики, динамический ряд (ВР) - последовательность чисел, элементы которой («уровни ряда») - значения статистического показателя (признака), протекающего во времени процесса. Например, исследуется изменение шероховатости поверхности при обработке с течением времени за счёт изменения состава и свойств СОЖ, геометрии режущей кромки инструмента и т.д. Здесь время или порядок обработки деталей имеют решающее значение. (Подробнее временные ряды рассмотрены в гл. 8).