Операторы в евклидовых пространствах
Линейные операторы, действующие в евклидовых пространствах, обладают рядом специальных свойств, которые весьма важны для приложений линейной алгебры в различных предметных областях. Мы остановимся только на основных вопросах этой теории, в частности, будем изучать теорию линейных операторов исключительно в вещественных пространствах с ортонормированными базисами, а именно в пространстве 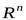 . Причём операторы будем считать преобразованиями, то есть будем изучать операторы
. Причём операторы будем считать преобразованиями, то есть будем изучать операторы 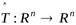 .
.
Сопряжённый оператор. Рассмотрим понятие оператора, сопряжённого к оператору 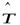 , действующему в евклидовом пространстве
, действующему в евклидовом пространстве 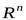 .
.
Определение 9.1. Пусть 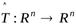 – некоторый линейный оператор. Оператор
– некоторый линейный оператор. Оператор 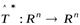 называетсясопряжённым к оператору
называетсясопряжённым к оператору 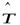 , если
, если 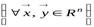 выполняется условие
выполняется условие
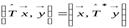 .
.  (9.1)
(9.1)
Теорема 9.1. Для любого линейного оператора 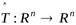 существует единственный сопряжённый оператор
существует единственный сопряжённый оператор 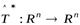 , который также является линейным.
, который также является линейным.
Д о к а з а т е л ь с т в о. 1) Пусть оператор 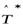 существует, докажем его единственность. Для этого предположим, что этот оператор не единственный, то есть существуют, например, два оператора
существует, докажем его единственность. Для этого предположим, что этот оператор не единственный, то есть существуют, например, два оператора 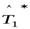 и
и 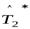 , удовлетворяющих определению 9.1. Тогда по формуле (9.1) имеем:
, удовлетворяющих определению 9.1. Тогда по формуле (9.1) имеем:
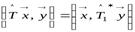 ,
, 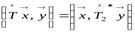 , (9.2)
, (9.2)
откуда получаем
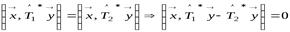 . (9.3)
. (9.3)
В силу того, что в определении 9.1 (в формуле (9.1)) вектор 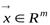 произволен, положим в равенстве (9.3)
произволен, положим в равенстве (9.3)
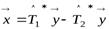 ,
,
получим
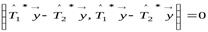 .
.
Так как скалярное произведение удовлетворяет аксиоме невырожденности, из последнего равенства имеем
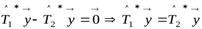 ,
,
откуда в силу произвольности вектора 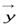 следует, что
следует, что 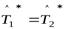 и единственность сопряжённого оператора доказана.
и единственность сопряжённого оператора доказана.
2) Докажем линейность сопряжённого оператора. Используя определение (9.1) и свойства скалярного произведения, получаем:
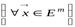 ,
, 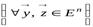 и
и 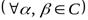
а) 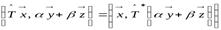 ;
;
б) 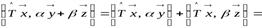
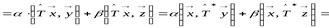
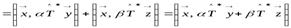 .
.
Из сравнения формул а) и б) следует линейность сопряжённого оператора 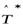 , а именно:
, а именно:
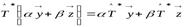 .
.
3) Докажем теперь существование сопряжённого оператора. Зафиксируем в пространстве 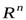 канонический базис
канонический базис 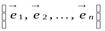 , и запишем векторы
, и запишем векторы 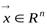 и
и 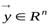 в виде их разложений по каноническому базису:
в виде их разложений по каноническому базису:
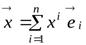 ;
; 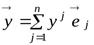 . (9.4)
. (9.4)
Рассмотрим вычисление левой и правой частей (9.1):
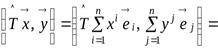
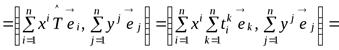
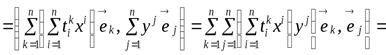
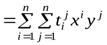 ;
;
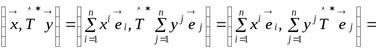
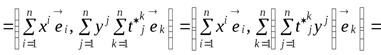
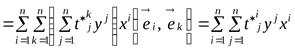 .
.
Сравнивая два последних равенства с учётом (9.1), получаем:
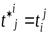 . (9.5)
. (9.5)
Итак, если матрица оператора 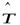 имеет вид
имеет вид
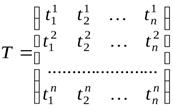 ,
,
то матрица сопряжённого оператора имеет вид
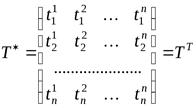 . (9.6)
. (9.6)
Из (9.6) следует, что матрица сопряжённого оператора 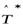 в любом ортонормированном базисе
в любом ортонормированном базисе  находится путем транспонирования матрицы оператора
находится путем транспонирования матрицы оператора  , что и доказывает существование сопряжённого оператора.
, что и доказывает существование сопряжённого оператора. 
Докажем теорему о свойствах оператора, сопряжённого линейному оператору.
Теорема 9.2. Справедливы следующие свойства сопряжённого оператора  :
: 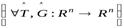 и
и 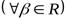
1) 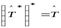 ; 2)
; 2) 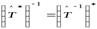 ;
;
3) 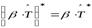 ; 4)
; 4) 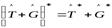 ; (9.7)
; (9.7)
5) 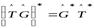 .
.
Д о к а з а т е л ь с т в о. Докажем первое соотношение. Пусть 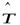 – произвольный линейный оператор. Для сопряжённого оператора
– произвольный линейный оператор. Для сопряжённого оператора 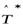 сопряжённым будет оператор
сопряжённым будет оператор 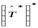 . Тогда:
. Тогда: 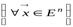
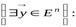
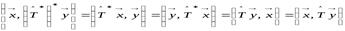 .
.
Последнее равенство выполняется при любом векторе 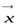 , то есть,
, то есть,
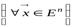
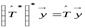 ,
,
откуда следует доказательство первого свойства.
Докажем второе соотношение. Для этого рассмотрим следующую цепочку преобразований:
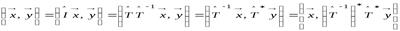 .
.
(9.8)
Из сравнения левой и правой частей равенства (9.8) следует доказательство второго свойства.
Остальные свойства доказываются аналогично. 
Самосопряжённые операторы. В приложениях большое значение имеют самосопряжённые операторы.
Определение 9.2. Линейный оператор 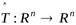 называетсясамосопряжённым, если
называетсясамосопряжённым, если 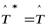 .
. 
Из определения следует, что для самосопряжённого оператора справедливо соотношение
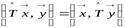 . (9.9)
. (9.9)
Так как матрица сопряжённого оператора 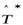 равна транспонированной матрице оператора
равна транспонированной матрице оператора 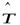 , то у самосопряжённого оператора элементы матрицы удовлетворяют равенству
, то у самосопряжённого оператора элементы матрицы удовлетворяют равенству 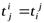 , то естьэлементы матрицы самосопряжённого оператора, симметричные относительно главной диагонали, равны. Такая матрица называется симметрической. По этой причине самосопряжённые операторы
, то естьэлементы матрицы самосопряжённого оператора, симметричные относительно главной диагонали, равны. Такая матрица называется симметрической. По этой причине самосопряжённые операторы 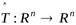 часто называютсясимметрическими.
часто называютсясимметрическими.
Самосопряжённые операторы обладают рядом свойств, которые нетрудно доказать, используя определение и свойства сопряжённого оператора.
1. Единичный оператор 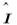 является самосопряжённым.
является самосопряжённым.
Д о к а з а т е л ь с т в о. Очевидно,
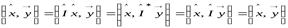 .
. 
2. Сумма самосопряжённых операторов является самосопряжённым оператором.
Д о к а з а т е л ь с т в о. Если 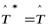 и
и 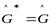 , то
, то
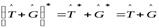 .
. 
3. Композиция самосопряжённых операторов является самосопряжённым оператором в том и только в том случае, если эти операторы коммутативны.
Д о к а з а т е л ь с т во. Напомним, что операторы называются коммутативными, если
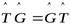 ,
,
или
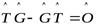 ,
,
где 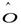 – нулевой оператор. Если
– нулевой оператор. Если 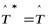 ,
, 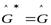 , то
, то
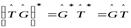 ,
,
что равно 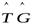 в том и только в том случае, если операторы коммутативны.
в том и только в том случае, если операторы коммутативны. 
4. Оператор 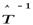 , обратный к невырожденному самосопряжённому оператору
, обратный к невырожденному самосопряжённому оператору 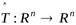 также самосопряжённый оператор.
также самосопряжённый оператор.
Д о к а з а т е л ь с т во. Действительно, если 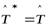 , то
, то
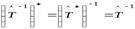 .
. 
5. Если 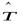 – самосопряжённый оператор, то произведение этого оператора на некоторое вещественное число
– самосопряжённый оператор, то произведение этого оператора на некоторое вещественное число 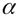 является самосопряжённым оператором.
является самосопряжённым оператором.
Д о к а з а т е л ь с т во. Из третьего свойства (9.7), имеем:
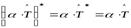 .
. 
Теорема 9.3. Собственные векторы самосопряжённого оператора 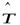 , действующего в пространстве
, действующего в пространстве 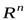 , соответствующие попарно различным собственным значениям, взаимно ортогональны.
, соответствующие попарно различным собственным значениям, взаимно ортогональны.
Д о к а з а т е л ь с т в о. Пусть 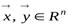 :
: 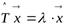 и
и 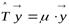 , причём
, причём 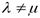 . Так как оператор самосопряжённый, то
. Так как оператор самосопряжённый, то 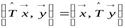 . Поэтому в левой и правой частях, соответственно, имеем:
. Поэтому в левой и правой частях, соответственно, имеем:
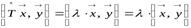 ;
;
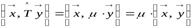 .
.
Откуда в силу 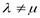 получаем:
получаем: 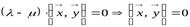 .
. 
Для самосопряжённых операторов справедлива следующая важная теорема.
Теорема 9.4. Все корни характеристического многочлена самосопряжённого оператора 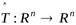 вещественные и различные.
вещественные и различные.
Д о к а з а т е л ь с т в о. В общем случае доказательство теоремы достаточно громоздкое. По этой причине приведём доказательство для случая оператора 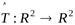 . Итак, пусть дан некоторый линейный оператор
. Итак, пусть дан некоторый линейный оператор 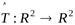 с матрицей
с матрицей 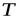 . Тогда характеристическое уравнение этого оператора имеет вид:
. Тогда характеристическое уравнение этого оператора имеет вид:
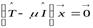
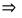
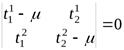 .
.
Раскрывая определитель, получаем характеристическое уравнение:
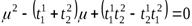 .
.
Решение этого уравнения находим по известной формуле:
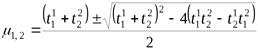 .
.
Дискриминант имеет вид:
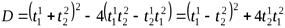 .
.
Первое слагаемое, очевидно, всегда положительно, а второе положительно, так как 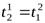 . Поэтому корни характеристического уравнения вещественные и различные.
. Поэтому корни характеристического уравнения вещественные и различные. 
Теорема 9.5. Пусть 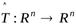 – самосопряжённый оператор. Тогда в пространстве
– самосопряжённый оператор. Тогда в пространстве 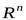 можно выбрать ортонормированный базис
можно выбрать ортонормированный базис
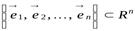
так, чтобы матрица оператора 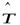 в этом базисе была диагональной.
в этом базисе была диагональной.
Д о к а з а т е л ь с т в о. По теореме 9.4 все корни характеристического многочлена самосопряжённого оператора вещественные и различные, а следовательно, по теореме 9.3 собственные векторы самосопряжённого оператора взаимно ортогональны. Систему собственных векторов, очевидно, можно нормировать. Но тогда эти векторы образуют базис пространства  , в котором оператор является оператором простой структуры, то есть имеет диагональную матрицу.
, в котором оператор является оператором простой структуры, то есть имеет диагональную матрицу. 
Ортогональные операторы и их свойства, геометрическая интерпретация. Рассмотрим определение и свойства важного класса операторов, действующих в пространстве 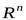 .
.
Определение 9.3. Оператор 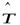 , действующий в пространстве
, действующий в пространстве 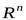 , называется ортогональным, если он сохраняет скалярное произведение, то есть
, называется ортогональным, если он сохраняет скалярное произведение, то есть
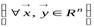
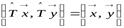 .
.  (9.10)
(9.10)
Из определения следует, что ортогональный оператор сохраняет нормы (длины) векторов и углы между ними.
Лемма 9.1. Оператор 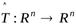 является ортогональным в том и только в том случае, если
является ортогональным в том и только в том случае, если 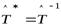 .
.
Д о к а з а т е л ь с т в о. Пусть 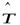 – ортогональный оператор. Тогда
– ортогональный оператор. Тогда
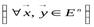
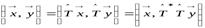 ,
,
откуда имеем: 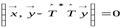 . Полагая
. Полагая 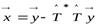 , получаем:
, получаем:
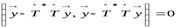
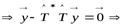
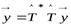
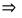
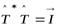
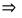
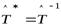 .
.
Пусть 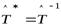 . Тогда имеем:
. Тогда имеем:
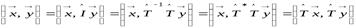 .
. 
Очевидно, что ортогональный оператор невырожден, то есть, его матрица имеет обратную матрицу.
Теорема 9.6 (о свойствах ортогональных операторов). Ортогональные операторы 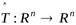 обладают следующими свойствами:
обладают следующими свойствами:
1) единичный оператор является ортогональным;
2) композиция ортогональных операторов также является ортогональным оператором;
3) оператор, обратный ортогональному оператору, также является ортогональным;
4) если 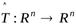 – ортогональный оператор, то оператор
– ортогональный оператор, то оператор 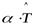 является ортогональным в том и только в том случае, если
является ортогональным в том и только в том случае, если 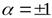 .
.
Д о к а з а т е л ь с т в о. 1. Доказательство этого свойства почти очевидно: 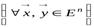
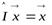
и
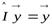
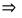
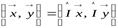 .
.
2. Пусть 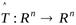 и
и 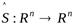 – ортогональные операторы. Тогда:
– ортогональные операторы. Тогда:
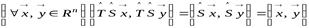 .
.
3. Пусть 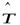 ортогональный оператор. Рассмотрим
ортогональный оператор. Рассмотрим 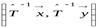 :
:
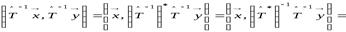
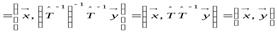 .
.
4. Пусть 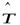 – ортогональный оператор. Тогда
– ортогональный оператор. Тогда
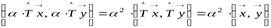
и
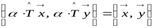
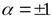 .
. 
Теорема 9.7 (критерий ортогональности оператора). Оператор 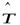 , действующий в пространстве
, действующий в пространстве 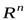 , является ортогональным в том и только в том случае, если он переводит хотя бы один ортонормированный базис в ортонормированный базис.
, является ортогональным в том и только в том случае, если он переводит хотя бы один ортонормированный базис в ортонормированный базис.
Д о к а з а т е л ь с т в о. Пусть 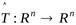 – ортогональный оператор. Тогда он, сохраняя скалярное произведение, переводит ортонормированный базис в ортонормированный базис.
– ортогональный оператор. Тогда он, сохраняя скалярное произведение, переводит ортонормированный базис в ортонормированный базис.
Пусть теперь оператор 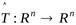 переводит ортонормированный базис
переводит ортонормированный базис
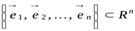
в новый ортонормированный базис
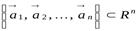 .
.
Тогда 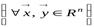
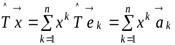
и
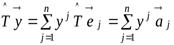 .
.
Откуда
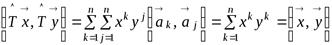 .
. 
Рассмотрим свойства матрицы ортогонального оператора.
Теорема 9.8. Система векторов-столбцов (строк) матрицы ортогонального оператора 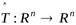 в любом ортонормированном базисе
в любом ортонормированном базисе
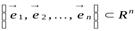
является ортонормированной.
Д о к а з а т е л ь с т в о. Пусть 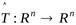 – некоторый ортогональный оператор и
– некоторый ортогональный оператор и 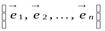 – некоторый ортонормированный базис. По теореме 9.9 система образов базисных векторов сама является ортонормированной, то есть
– некоторый ортонормированный базис. По теореме 9.9 система образов базисных векторов сама является ортонормированной, то есть 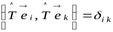 . Поэтому для столбцов матрицы оператора
. Поэтому для столбцов матрицы оператора
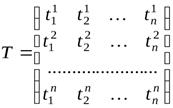 ,
,
(как векторов арифметического пространства 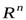 ) имеем:
) имеем:
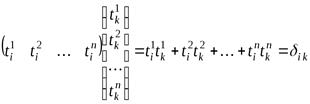 . (9.11)
. (9.11)
Аналогичное свойство справедливо и для строк матрицы  :
:
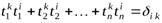 .
.  (9.12)
(9.12)
Теорема 9.9. Матрица ортогонального оператора 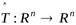 в любом ортонормированном базисе удовлетворяет условию
в любом ортонормированном базисе удовлетворяет условию
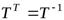 . (9.13)
. (9.13)
Д о к а з а т е л ь с т в о. Пусть 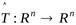 – ортогональный оператор. Так как матрицы операторов
– ортогональный оператор. Так как матрицы операторов 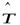 и
и 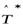 связаны соотношениями
связаны соотношениями
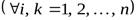
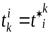 ,
,
откуда для матрицы оператора 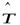 получаем (9.11).
получаем (9.11).
Обратно, пусть выполнено соотношение (9.11). Тогда 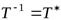 , откуда и следует, что оператор
, откуда и следует, что оператор 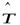 является ортогональным.
является ортогональным. 
Определение 9.4. Матрица 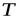 , для которой выполняется свойство(9.13), называется ортогональной.
, для которой выполняется свойство(9.13), называется ортогональной. 
Приведём некоторые теоремы о свойствах ортогонального оператора.
Теорема 9.10. Собственные значения ортогонального оператора 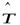 действующий в пространстве
действующий в пространстве 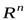 , равны
, равны 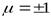 .
.
Д о к а з а т е л ь с т в о. Пусть 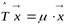 . Тогда
. Тогда
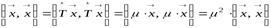 .
.
Так как по определению 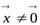 , то
, то 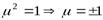 .
. 
Теорема 9.11. Определитель ортогональной матрицы 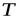 равен
равен
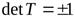 .
.
Д о к а з а т е л ь с т в о. Для ортогональной матрицы выполняется равенство 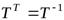 . Поэтому
. Поэтому 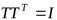 . Тогда
. Тогда
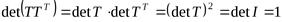
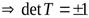 .
.