II.I. Определение форм и частот колебаний

Для круглой пластины для амплитудной функции 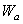следует перейти к полярным координатам 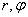. В этих координатах оператор Лапласа имеет вид

Таким образом, в полярных координатах принимает уравнения колебаний имеют вид

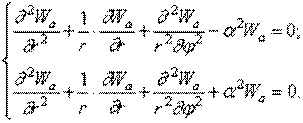
Решения этих уравнений, соответствующие колебаниям пластины с n узловыми диаметрами, можно представить в виде

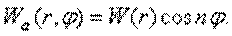
После подстановки этого выражения приходим к уравнениям:

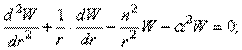
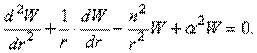
Решениями последних уравнений являются бесселевы функции порядка 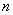первого 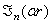и второго 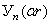рода и модифицированные бесселевы функции 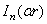, 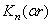. Таким образом, общее выражение амплитудной функции с 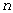узловыми диаметрами таково:

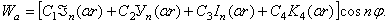
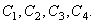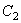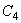Для кольцевой пластинки имеются четыре граничных условия (по два на каждом краю), которые образуют однородную систему уравнений относительно констант Для сплошной пластинки равны нулю коэффициенты и при функциях, стремящихся к бесконечности при 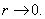Граничные условия на внешнем контуре пластинки образуют в этом случае однородную систему уравнений относительно 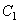и 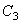. Частотное уравнение получается путем приравнивания нулю определителя системы.

Рассмотрим колебания свободной сплошной круглой пластинки. В этом случае на контуре должны выполняться условия:

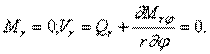
Изгибающий момент определяется формулой

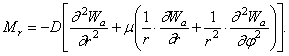
Поперечная сила:

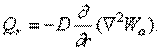
Крутящий момент:

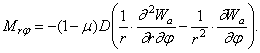
Таким образом, граничные условия имеют вид

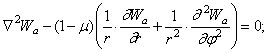
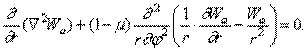
Учитывая, что 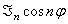является решением уравнения 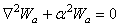, а 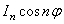- уравнения 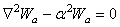, находим

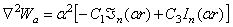
При подстановке вместо 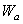его выражения

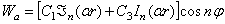
учтем правила дифференцирования функций Бесселя:

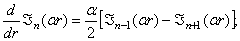
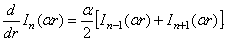
В результате приходим к уравнениям

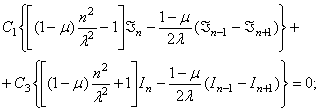
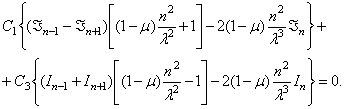
Здесь аргументом всех бесселевых функций является величина 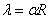, где 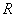- радиус пластинки.

Значения 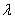, обращающие в нуль определитель полученной системы, связаны с собственными частотами равенством

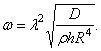
Если ограничиться формами колебаний без узловых окружностей, то значениям 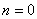и 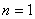соответствуют смещения пластинки как жесткой и нулевые частоты. При 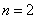(два узловых диаметра) частотное уравнение можно привести к виду

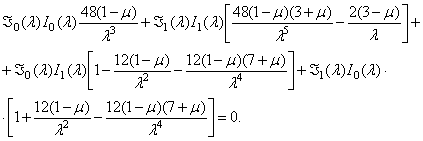
При 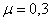наименьший корень этого уравнения 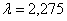и соответствующая частота собственных колебаний

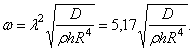
Для заделанной по контуру пластинки граничные условия

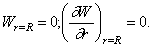
Частотное уравнение

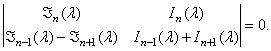
II.II. Бегущие волны в круглых пластинках

Рассмотренные выше собственные колебания круглых пластинок описываются уравнением

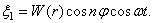
Они соответствуют стоячим волнам на поверхности пластинки, при которых узловые диаметры неподвижны.

Наряду с (330) решением уравнения движения является также выражение

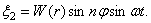
Но поскольку уравнение движения линейно, то их сумма и разность также являются его решениями:

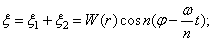
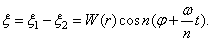
Эти выражения представляют собой уравнения бегущих волн. Первое выражение соответствует вращению всей картины деформаций вокруг оси симметрии пластинки в направлении возрастания угла 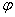с угловой скоростью 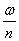. Второе выражение соответствует движению волны с той же скоростью в противоположном направлении.

Если имеются внешние нагрузки, вращающиеся по периферии пластинки со скоростью, близкой к скорости 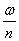распространения собственных колебаний, то такие нагрузки вызовут большие резонансные колебания пластинки.

Практически движущаяся по круглой пластинке нагрузка осуществляется в дисках турбомашин благодаря вращению диска при неподвижной в пространстве нагрузке, обусловленной неравномерностью давления рабочего тела по окружности.

Критические скорости вращения диска 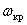могут быть найдены, если известны частоты его собственных колебаний 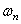, по формуле

,

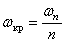где 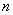- число узловых диаметров при свободных колебаниях с частотой .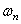