Задачи дробно-линейного программирования

Общая задача дробно-линейного программирования состоит в определении максимального (минимального) значения функции

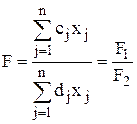
при условиях

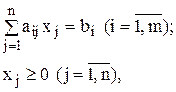
где c_j, d_j, b_i и a_ij– постоянные числа, 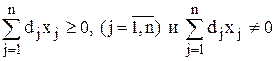в области неотрицательных решений системы линейных уравнений, задающих ограничения. Предположение, что 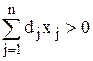не нарушает общности задачи, поскольку в том случае, когда эта величина отрицательна, минус можно отнести к числителю.

Сформулированная задача может быть сведена к задаче линейного программирования. Для этого следует обозначить

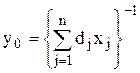
и ввести новые переменные

.

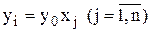Используя введенные обозначения, исходную задачу сведем к следующей - найти максимум (минимум) функции

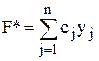
при условиях

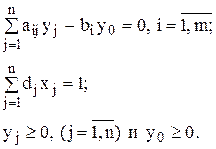
Построенная задача является задачей линейного программирования, следовательно, ее решение можно найти известными методами. Зная оптимальный план этой задачи, на основе соотношений 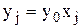, получаем оптимальный план исходной задачи.

Пример . Для производства двух видов изделий A и В используются два типа технологического оборудования. Первое изделие проходит обработку только на втором типе оборудования, второе - на первом и на втором. Время обработки каждого из изделий на оборудовании данного типа приведено в табл. 9. Там же указаны затраты, связанные с производством одного изделия каждого вида.

Таблица 9

Тип оборудования	Затраты времени (ч) на обработку одного изделия
A	B
I
II
Затраты на производство Одного изделия

Оборудование II типа предприятие может использовать не более 52 часов. При этом оборудование I типа целесообразно использовать не менее 16 часов. Требуется определить, сколько изделий каждого вида следует изготовить, чтобы себестоимость одного изделия была минимальной.

Составим математическую модель задачи. За x₁ обозначим количество выпускаемых изделий вида A, за x₂ – количество изделий вида B. Себестоимость определяется следующим образом: С=З/K, где К – количество выпускаемых изделий, З - общие затраты на их производство. Тогда получим следующую задачу дробно-линейного программирования:

;

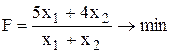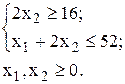
Преобразуем ограничения-неравенства данной задачи в равенства:

;

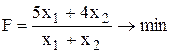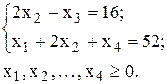
Сведем данную задачу к задаче линейного программирования. Для этого обозначим 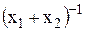через y₀ и введем новые переменные .

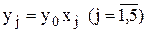В результате приходим к следующей задаче: найти минимум функции

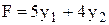
при условиях

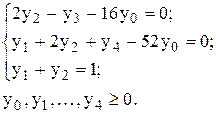
Система ограничений задачи содержит всего одну базисную переменную y₄. Поэтому составим расширенную задачу путем введения двух искусственных переменных y₅ и у₆. :

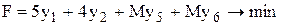
при условиях

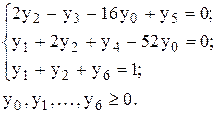
Решение задачи методом искусственного базиса приведено в табл. 10.

Таблица 10

xd	cd	b						M	M
y1	y2	y3	y4	y0	y6	y5
Y5	М			2	-1		-16
y4							-52
y6	М
	-5	-4
			-1		-16
y2					-1/2		-8
y4			1				-36
y6	M				1/2		-6
	-1		-2		-32
M			1/2		-6
y2					-1/2		-8
y1							-36
y6	M				-1/2	-1	30
			-16/3		-220
M			-1/2	-1
y2		8/30			-19/30	-8/30
y1		36/30			12/30	-6/30
y0		1/30			-1/60	-1/30
220/30			-12/30	-72/30

Из таблицы видно, что оптимальным планом задачи является

.

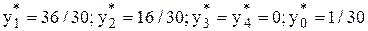Учитывая, что 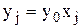, находим оптимальный план исходной задачи:

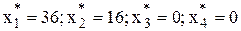. F(X^*)=220/30.