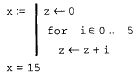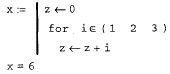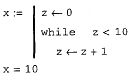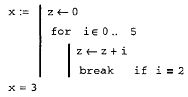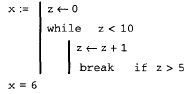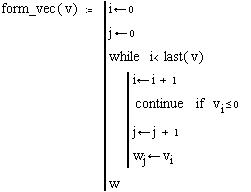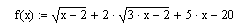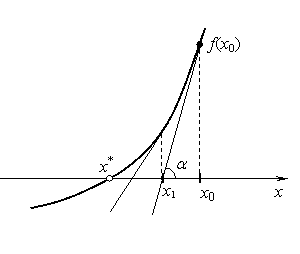
Рисунок 5 – Метод Ньютона.
Пусть нам известно начальное приближение к корню 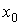 (вопрос выбора начального приближение будет подробно рассмотрен ниже). Проведем в этой точке касательную к кривой
(вопрос выбора начального приближение будет подробно рассмотрен ниже). Проведем в этой точке касательную к кривой 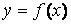 (рис. 5). Эта касательная пересечет ось
(рис. 5). Эта касательная пересечет ось
абсцисс в точке
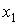
, которую будем рассматривать в качестве следующего приближения. Значение
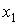
легко найти из рисунка:
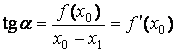 ,
,
выражая отсюда 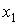 , получим
, получим
 .
.
Аналогично могут быть найдены и следующие приближения. Формула для k+1-го приближения имеет вид
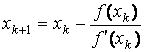 ,
, 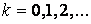 (12)
(12)
Из формулы (12) вытекает условие применимости метода: функция 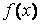 должна быть дифференцируемой и
должна быть дифференцируемой и 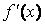 в окрестности корня не должна менять знак.
в окрестности корня не должна менять знак.
Для окончания итерационного процесса могут быть использованы условия (9) или (11).
1.5 Пакет MathCad. Использование программных фрагментов
Mathcad —это популярная система компьютерной математики, предназначенная для автоматизации решения массовых математических задач в самых различных областях науки, техники и образования. Название системы происходит от двух слов — MATHmatica (математика) и CAD (Computer Aided Design — системы автоматического проектирования, или САПР). Так что вполне правомерно считать Mathcad математическими САПР.[1, стр 9]
Как интегрированная система Mathcad 2000 содержит следующие основные компоненты:
1. Редактор документов — редактор с возможностью вставки математических выражений, шаблонов графиков и текстовых комментариев;
2. MathConnex — системный интегратор, обеспечивающий интеграцию Mathcad с рядом иных программных продуктов;
3. Центр ресурсов — система управления ресурсами системы;
4. Электронные книги — электронные книги с описанием типовых расчетов в различных областях науки и техники;
5. Справочная система — система для получения справочных данных по тематическому и индексному каталогу, а также для поиска нужных данных по ключевому слову или фразе;
6.Быстрые шпаргалки QuickSheets — короткие примеры с минимальными комментариями, описывающие применение всех встроенных операторов и функций системы;
7. Броузер Интернета — собственное средство выхода в Интернет.[1, стр.15]
Программа в Mathcad есть выражение, в свою очередь, состоящее из других выражений. Программы Mathcad содержат конструкции, во многом подобные программным конструкциям языков программирования: условные
передачи управления, операторы циклов, области видимости переменных, использование подпрограмм и рекурсии.
Написание программ в Mathcad позволяет решить такие задачи, которые невозможно или очень трудно решить другим способом.
Программа Mathcad есть частный случай выражения Mathcad. Подобно любому выражению, программа возвращает значение, если за ней следует знак равенства. Точно так же, как переменную или функцию можно определить через выражение, их можно определить и с помощью программы.
Главным различием между программой и выражением является способ задания вычислений. При использовании выражения алгоритм получения ответа должен быть описан одним оператором. В программе может быть использовано столько операторов, сколько нужно. Можно рассматривать программу как “составное выражение.
Условный оператор (if, otherwise)
Действие условного оператора if состоит из двух частей. Сначала проверяется логическое выражение (условие) справа от него. Если оно истинно, выполняется выражение слева от оператора if. Если ложно - ничего не происходит, а выполнение программы продолжается переходом к ее следующей строке. Вставить условный оператор в программу можно следующим образом:
1. Если необходимо, введите левую часть выражения и оператор присваивания.
2. Создайте новую строку программного кода, нажав на панели Programming (Программирование) кнопку Add Line (Добавить строку).
3. Нажмите кнопку условного оператора if.
4. Справа от оператора if введите условие. Пользуйтесь логическими операторами, вводя их с панели Boolean (Булевы операторы).
5. Выражение, которое должно выполняться, если условие оказывается выполненным, введите слева от оператора if.
6. Если в программе предусматриваются дополнительные условия, добавьте в программу еще одну строку нажатием кнопки Add Line и введите их таким же образом, используя оператор if или otherwise.
Оператор otherwise используется совместно с одним или несколькими условными операторами if и указывает на выражение, которое будет выполняться, если ни одно из условий не оказалось истинным.
Операторы цикла (for, while, break, continue)
В языке программирования MathCAD имеются два оператора цикла: for и while. Первый из них дает возможность организовать цикл по некоторой переменной, заставляя ее пробегать некоторый диапазон значений. Второй создает цикл с выходом из него по некоторому логическому условию. Чтобы вставить в программный модуль оператор цикла:
1. Создайте в программном модуле новую линию.
2. Вставьте один из операторов цикла for или while нажатием одноименной кнопки на панели Programming (Программирование).
3. Если выбран оператор for, то вставьте в соответствующие местозаполнители имя переменной и диапазон ее значений, а если while - то логическое выражение, при нарушении которого должен осуществляться выход из цикла.
4. В нижний местозаполнитель введите тело цикла, т. е. выражения, которые должны выполняться циклически.
5. При необходимости дополните программу другими строками и введите в них нужный код.
Диапазон значений переменной в условии цикла for можно задать как с помощью диапазона ранжированной переменной, так и с помощью вектора.
Оператор цикла for с ранжированной переменной
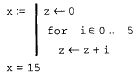
Оператор цикла for с вектором
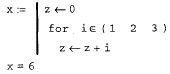
Оператор цикла while ,
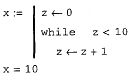
Иногда необходимо досрочно завершить цикл, т. е. не по условию в его заголовке, а в некоторой строке в теле цикла. Для этого предназначен оператор break. Например, в листинге, как только значение переменной цикла i достигает 2, цикл, благодаря оператору break в последней строке программного модуля, прерывается. Соответственно, значение переменной х остается равным 0+1+2=3.
Оператор break внутри цикла for
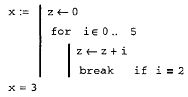
Оператор break внутри цикла while
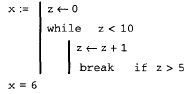
Чтобы четче обозначить границы завершения тела цикла, в его конце может использоваться дополнительная строка с оператором continue, который вводится одноименной кнопкой панели. Обычно используется для продолжения выполнения цикла путем возврата в начало тела цикла. Составим программу-функцию, формирующую новый вектор из положительных проекций исходного вектора.
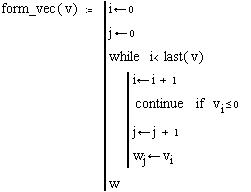
2 Алгоритмический анализ задачи
Постановка задачи.
Задание состоит из трех частей.
1. Расчетно – графическая часть
Исходные данные:
· Вид нелинейного уравнения
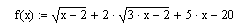
· Аргумент функции должен быть представлен в виде дискретной переменной. Диапазон изменения переменной выбрать самостоятельно.
Результаты:
· Значения функции, ее первой и второй производных на всем диапазоне значений аргумента функции
· График функции, ее первой и второй производных
· Значения корней уравнения, полученных с помощью
а) трассировки и нанесения маркеров
b) стандартной функции поиска корней уравнения
2. Программная часть
Исходные данные:
· Результаты расчетно – графической части
· Численные методы
a) половинного деления
b) хорд
c) касательных
Результаты:
Значения корней уравнения, полученных каждым численным методом и с разной степенью точности
3. Исследовательская часть
Анализ количества итераций от точности численного метода
Исходные данные:
·
Вектор точности вычисления корня уравнения
Результаты:
· Количество итераций вычисления корня уравнения для каждой величины точности
· График зависимостей количества итераций от точности вычислений
2.2 Графическая схема алгоритма
Планируя процесс вычисления корней нелинейного уравнения составляем последовательность действий необходимых расчетов, который изложен в графической схеме алгоритма (рисунок 6).
| Определение нелинейного уравнения f(x) |
| Нахождение первой и второй производной функции |
| Определение аргумента, нахождение значения функции, её первой и второй производной |
| График и функции, её первой и второй производной |
| Определение корня стандартной функцией |
| определение функции метода половинного деления |
| определение функции метода хорд |
Рисунок 6. Алгоритм решения задачи.
| определение функции метода касательных |
| Определения корня с заданной степенью точности |
| Определение вектора точности вычисления корня уравнен |
| Расчет количества итераций различными методами |
| Вывод графика зависимости кол-ва итераций |
Рисунок 6. Алгоритм решения задачи.
При вычислении корней нелинейного уравнения первоначально, в соответствии с поставленной задачей, был разработан алгоритм её решения. В графической схеме алгоритма был отражен процесс решения задачи, это и ввод исходных данных, и выполнение расчетно - графической части, и составление программного фрагмента, и
проведение исследований по анализу количества итераций, и конечно вывод результатов.
Описание документа MathCAD

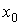 (вопрос выбора начального приближение будет подробно рассмотрен ниже). Проведем в этой точке касательную к кривой
(вопрос выбора начального приближение будет подробно рассмотрен ниже). Проведем в этой точке касательную к кривой 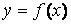 (рис. 5). Эта касательная пересечет ось
(рис. 5). Эта касательная пересечет ось 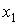 , которую будем рассматривать в качестве следующего приближения. Значение
, которую будем рассматривать в качестве следующего приближения. Значение 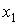 легко найти из рисунка:
легко найти из рисунка: 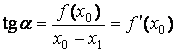 ,
,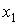 , получим
, получим .
.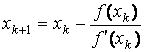 ,
, 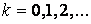 (12)
(12)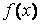 должна быть дифференцируемой и
должна быть дифференцируемой и 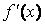 в окрестности корня не должна менять знак.
в окрестности корня не должна менять знак.