Теорема деления тензоров (критерий тензорности)
Рассмотрим удобный критерий для характеристики геометрических и физических величин при помощи тензоров. Пусть некоторая величина в прямоугольных координатах 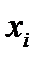 и
и 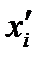 определяется при помощи
определяется при помощи 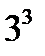 чисел
чисел 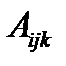 и
и 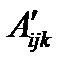 соответственно, и пусть для любых трех векторов
соответственно, и пусть для любых трех векторов 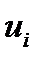 ,
, 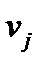 ,
, 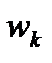 справедливо равенство:
справедливо равенство:
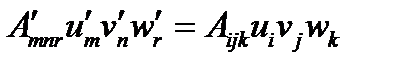 (114)
(114)
т.е. левая и правая части равенства – скаляры. Тогда можно показать, что 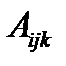 и
и 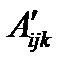 являются компонентами тензора 3-его ранга относительно координатных систем
являются компонентами тензора 3-его ранга относительно координатных систем 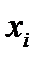 и
и 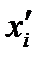 соответственно. Для доказательства выразим в равенстве (114) компоненты векторов в старой системе
соответственно. Для доказательства выразим в равенстве (114) компоненты векторов в старой системе 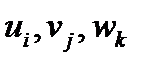 через компоненты в новой системе
через компоненты в новой системе 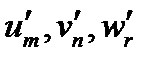 :
: 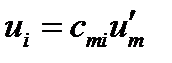 ,
, 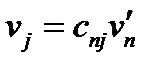 ,
, 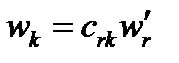 и подставим в (114):
и подставим в (114): 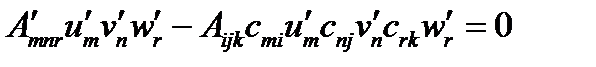 , или
, или
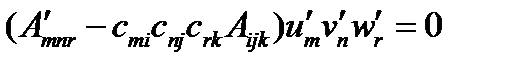 (115)
(115)
Левая часть этого равенства представляет собой тройную сумму по индексам 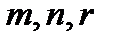 . Она может тождественно равняться нулю лишь в том случае, когда обращаются в нуль все ее коэффициенты при компонентах векторов, т.е. когда для всех значений индексов
. Она может тождественно равняться нулю лишь в том случае, когда обращаются в нуль все ее коэффициенты при компонентах векторов, т.е. когда для всех значений индексов 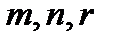 выражение в скобках равно нулю:
выражение в скобках равно нулю: 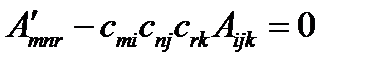 . Отсюда получим:
. Отсюда получим: 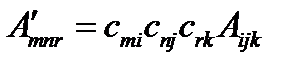 (116)
(116)
т.е. величины 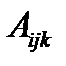 в старой системе координат преобразуются в величины
в старой системе координат преобразуются в величины 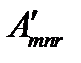 в новой системе так же, как компоненты тензора 3-его ранга. Аналогично можно провести рассуждения и для обратного перехода от новой системы к старой. Следовательно, приходим к выводу, что
в новой системе так же, как компоненты тензора 3-его ранга. Аналогично можно провести рассуждения и для обратного перехода от новой системы к старой. Следовательно, приходим к выводу, что 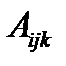 – это тензор 3-его ранга.
– это тензор 3-его ранга.
Аналогично можно показать, что 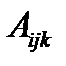 – тензор 3-его ранга, если известно, что
– тензор 3-его ранга, если известно, что 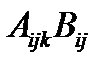 есть вектор при любом выборе тензора 2-ого ранга
есть вектор при любом выборе тензора 2-ого ранга 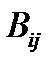 .
.
Для краткости мы рассмотрели лишь тензор 3-его ранга, но можно получить обобщение для тензоров любого ранга. Изложенный критерий является частным случаем известной в тензорной алгебре теоремы деления тензоров.
§18. 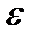 - тензор Леви-Чивиты (единичный тензор 3-го ранга).
- тензор Леви-Чивиты (единичный тензор 3-го ранга).
Во многих случаях очень удобным оказывается использование так называемого символа Леви-Чивиты:
 (117)
(117)
Круговые перестановки – это 123, 231, 312. Некруговые перестановки – это 132, 213, 321. Следствием этого определения являются следующие соотношения:
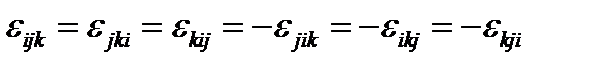 (118)
(118)
Справедливость их следует из того, что перестановки 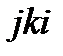 и
и 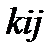 являются круговыми из первоначальной перестановки
являются круговыми из первоначальной перестановки 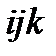 , а перестановки
, а перестановки 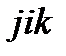 ,
, 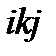 ,
, 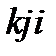 круговыми не являются.
круговыми не являются.
Приведем полезные соотношения, связанные с символом Леви-Чивиты:
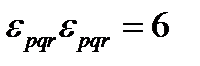 ,
, 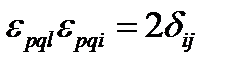 ,
, 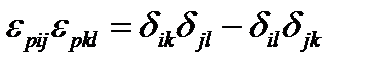 (119)
(119)
Рассмотрим применение символа Леви-Чивиты. Как известно из курса векторной алгебры, смешанное произведение трех векторов 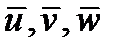 записывается в виде определителя:
записывается в виде определителя:
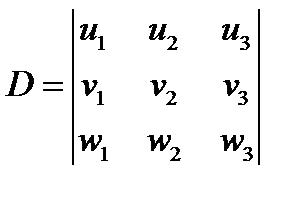 (120)
(120)
С помощью символа Леви-Чивиты смешанное произведение записывается компактно:
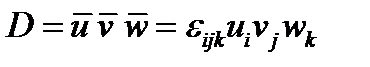 (121)
(121)
Чтобы доказать это, проведем суммирование по индексам 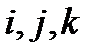 , принимая во внимание определение (117):
, принимая во внимание определение (117):
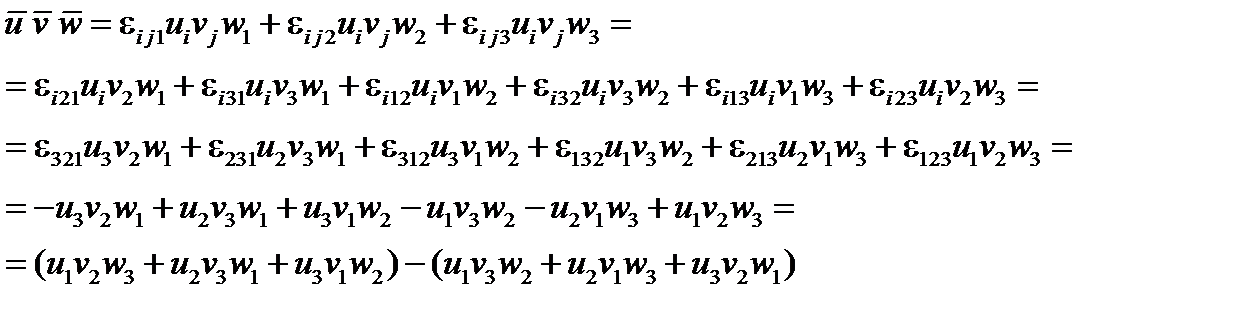
С другой стороны, если раскрыть определитель (120), то получим то же самое.
Как известно, смешанное произведение, т.е. определитель (120), положительно, если тройка перемножаемых векторов 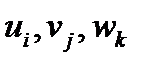 и тройка базисных векторов имеют одинаковую ориентацию (например, обе – правые). В противном случае смешанное произведение отрицательно. Отсюда следует, что при переходе от правой системы координат к левой и наоборот, смешанное произведение меняет знак. Такие величины называются псевдоскалярами, в отличие от истинных скаляров, которые не меняются при любых преобразованиях. В частности, модуль смешанного произведения, т.е. объем параллелепипеда, построенного на перемножаемых векторах, является истинным скаляром.
и тройка базисных векторов имеют одинаковую ориентацию (например, обе – правые). В противном случае смешанное произведение отрицательно. Отсюда следует, что при переходе от правой системы координат к левой и наоборот, смешанное произведение меняет знак. Такие величины называются псевдоскалярами, в отличие от истинных скаляров, которые не меняются при любых преобразованиях. В частности, модуль смешанного произведения, т.е. объем параллелепипеда, построенного на перемножаемых векторах, является истинным скаляром.
Выведем закон преобразования символа Леви-Чивиты при преобразованиях координат. Обозначим компоненты символа Леви-Чивиты в новой координатной системе через 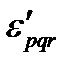 , а компоненты векторов, участвующих в смешанном произведении, через
, а компоненты векторов, участвующих в смешанном произведении, через 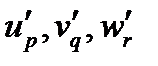 . В новой координатной системе смешанное произведение запишется как
. В новой координатной системе смешанное произведение запишется как 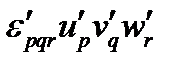 , и имеет место равенство:
, и имеет место равенство:
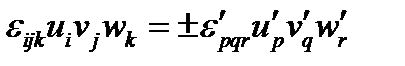 , (122)
, (122)
где знак плюс берется, если при преобразовании координат ориентация базисных векторов не меняет знак, и знак минус – в противном случае. Вспоминая закон преобразования векторов (формулы (40), (41)), получим из (122): 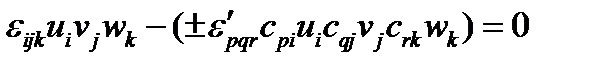 , или
, или 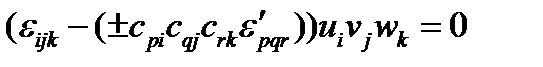 .
.
Рассуждая теперь так же, как в параграфе 17, получим:
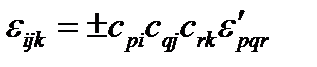 (123)
(123)
Аналогично получается и обратная формула:
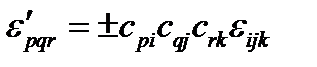 (124)
(124)
Этими формулами определяется закон преобразования символа Леви-Чивиты. С точностью до знака он совпадает с законом преобразования тензора 3-его ранга.
Если при преобразовании ориентация системы координат не меняется, т.е. если, например, правая система остается правой, то в формулах (123) и (124) нужно брать знак плюс, если же правая система переходит в левую, или наоборот, – то знак минус. Геометрический объект, преобразующийся по формулам (123) и (124), называется псевдотензором, в данном случае 3-его ранга. Если ограничиться только правыми системами координат, что мы и будем подразумевать в дальнейшем за небольшими исключениями, то символ Леви-Чивиты будет истинным тензором 3-его ранга. Он так и называется тензором Леви-Чивиты или 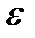 - тензором. Из определений (117) и (118) следует, что
- тензором. Из определений (117) и (118) следует, что 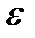 - тензор является полностью антисимметричным по всем трем индексам.
- тензор является полностью антисимметричным по всем трем индексам.
Векторное произведение тоже очень просто записывается с помощью 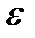 - тензора:
- тензора:
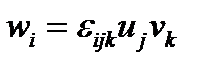 (125)
(125)
В курсе линейной алгебры векторное произведение определялось как вектор. Это не совсем так с точки зрения определения вектора, данного в параграфе 2. Там мы определяли вектор как объект, компоненты которого преобразуются по формулам (40), (41). Найдем закон преобразования компонент векторного произведения, имея в виду, что символ Леви-Чивиты преобразуется по формулам (123), (124), а векторы 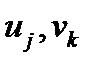 – по формулам (40), (41):
– по формулам (40), (41):
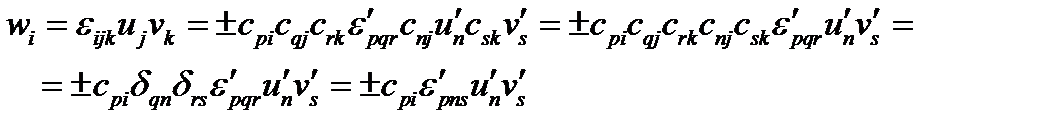
Поскольку в новой системе координат векторное произведение определяется той же формулой (125), то 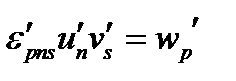 , и тогда
, и тогда
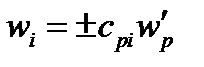 (126)
(126)
Аналогично получаем формулу обратного перехода, тоже с двумя знаками: плюс и минус:
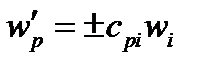 (127)
(127)
| Рис. 9а) |
Примерами аксиальных или псевдовекторов являются угловая скорость, момент количества движения, момент силы, ротор полярного вектора, напряженность и индукция магнитного поля. В то время как перемещение, скорость, ускорение, сила – это все полярные векторы. Аксиальный вектор характеризует вращение вокруг некоторой оси и поэтому изображается отрезком прямой определенной длины параллельно оси с указанием направления вращения вокруг оси. На рис. 9 показано символическое изображение полярного вектора (а) и аксиального вектора (б):
| Рис. 9б) |
Допустим, что мы перешли от правой системы координат к левой посредством преобразования 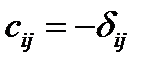 , т.е. изменили направление всех осей напротивоположные (рис. 10). Новые компоненты полярного вектора будут равны:
, т.е. изменили направление всех осей напротивоположные (рис. 10). Новые компоненты полярного вектора будут равны:
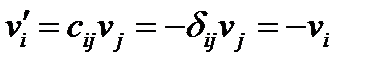 (128)
(128)
 |
 |
| Рис. 10 |
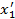 |
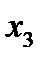 |
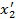 |
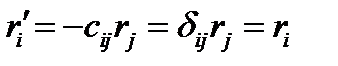 (129)
(129) т.е. аксиальный вектор не изменился.
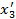 |
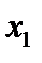 |
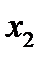 |
Бивектор.
Антисимметричный тензор 2-ого ранга называется иначе бивектором. Такое название проистекает из того, что этому тензору можно поставить в соответствие вектор (точнее аксиальный вектор, т.е. псевдовектор). Пусть 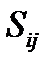 – антисимметричный тензор 2-го ранга. Его матрица имеет вид:
– антисимметричный тензор 2-го ранга. Его матрица имеет вид:
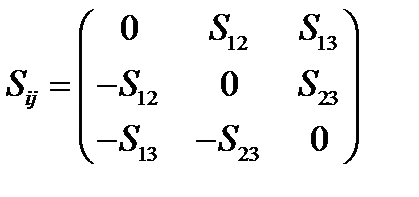 (130)
(130)
Такой тензор имеет всего три, как говорят, существенные компоненты 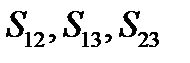 . Найдем компоненты тензора
. Найдем компоненты тензора 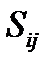 в какой-либо другой системе, используя закон преобразования тензоров 2-ого ранга (70) и принимая во внимание его антисимметричность:
в какой-либо другой системе, используя закон преобразования тензоров 2-ого ранга (70) и принимая во внимание его антисимметричность:
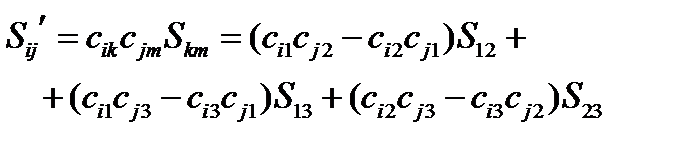 (131)
(131)
Как было показано в параграфе 12, свойство антисимметричности не зависит от системы координат. Поэтому и в новой системе существенными будут только три компоненты:
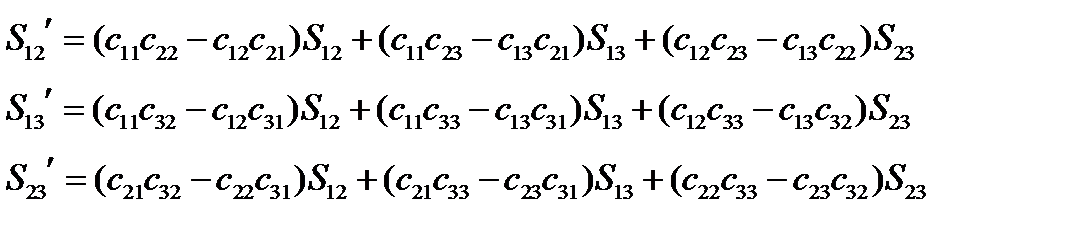 (132)
(132)
Проанализируем сначала первую из этих формул. В правой части в скобках выражения равны минорам элементов третьей строки матрицы преобразования 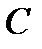 (см. §3):
(см. §3):
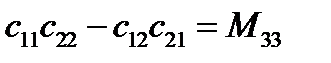 ,
, 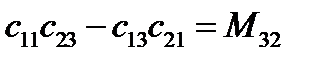 ,
, 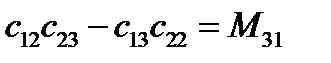 (133)
(133)
или, заменяя миноры 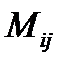 алгебраическими дополнениями
алгебраическими дополнениями 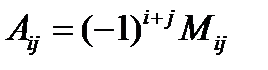 , получим:
, получим:
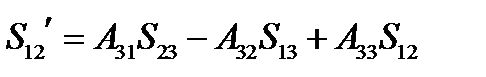 (134)
(134)
Аналогично для двух других существенных компонент получим:
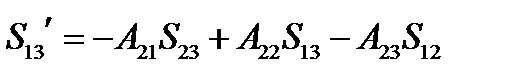 ,
, 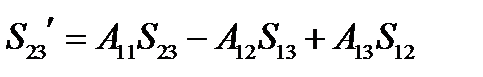 (135)
(135)
В задаче 6 параграфа 8 было показано, что каждый элемент матрицы преобразования 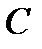 равен с точностью до знака своему алгебраическому дополнению. С учетом этого получаем:
равен с точностью до знака своему алгебраическому дополнению. С учетом этого получаем:
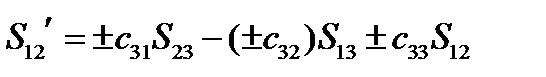 ,
,
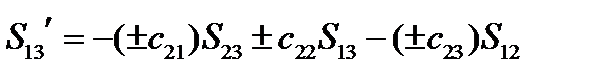 (136)
(136)
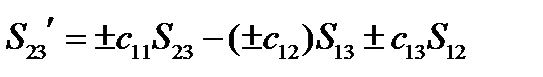
Если при преобразовании координат ориентация новой системы не изменится, то в (136) следует брать знак плюс. Тогда:
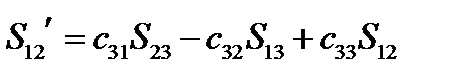
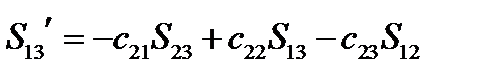 (137)
(137)
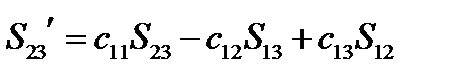
Эти выражения напоминают закон преобразования компонент вектора. Последнее будет особенно заметно, если переобозначить существенные компоненты тензора 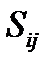 так:
так: 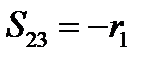 ,
, 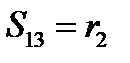 ,
, 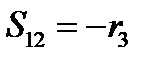 . Соответственно в новой системе:
. Соответственно в новой системе: 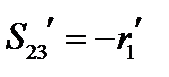 ,
, 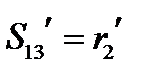 ,
, 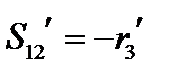 . Тогда формулы (137) принимают знакомый вид:
. Тогда формулы (137) принимают знакомый вид:
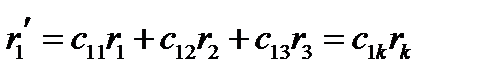
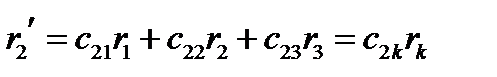 (138)
(138)
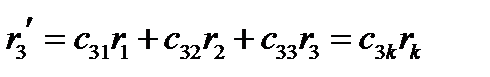
или коротко: 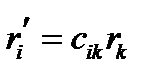 (139)
(139)
Если же ориентация новой системы изменилась, то:
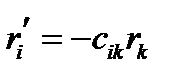 (140)
(140)
Объединяя эти две формулы, окончательно получим:
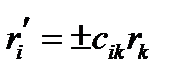 (141)
(141)
Теперь видно, что три величины 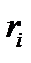 являются компонентами аксиального вектора. Матрица антисимметричного тензора 2-ого ранга (бивектора) выглядит теперь так:
являются компонентами аксиального вектора. Матрица антисимметричного тензора 2-ого ранга (бивектора) выглядит теперь так:
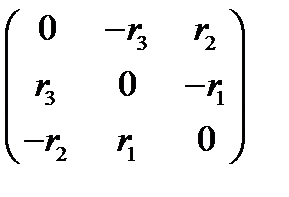 (142)
(142)
Таким образом, всякий антисимметричный тензор 2-ого ранга эквивалентен аксиальному вектору. В правосторонних системах координат это будет истинный вектор. Используя  - тензор, связь между вектором
- тензор, связь между вектором 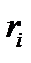 и бивектором
и бивектором 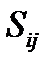 можно записать так:
можно записать так:
 (143)
(143)
Чтобы убедиться в этом, распишем подробно:
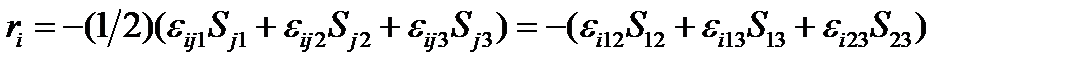 . Тогда:
. Тогда: 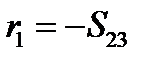 ,
, 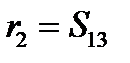 ,
, 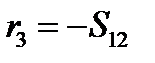 , что совпадает с введенными выше компонентами вектора
, что совпадает с введенными выше компонентами вектора  .
.
По формуле (143) можно найти аксиальный вектор 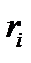 , зная бивектор
, зная бивектор 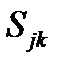 . Можно получить и обратную формулу. Для этого умножим обе части (143) на
. Можно получить и обратную формулу. Для этого умножим обе части (143) на 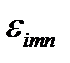 :
: 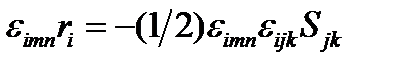 .
.
Воспользуемся третьей формулой (119):
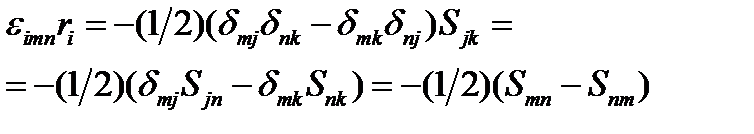
или с учетом антисимметричности 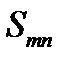 :
: 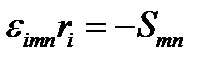 . Окончательно:
. Окончательно: 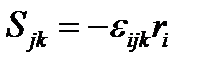 (144)
(144)
Эта формула позволяет найти бивектор 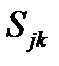 , если известен вектор
, если известен вектор 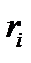 .
.
