Л а б о р а т о р н а я р а б о т а 3

ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ТИПОВЫХ ДИНАМИЧЕСКИХ ЗВЕНЬЕВ

Ц Е Л Ь Р А Б О Т Ы - экспериментальное определение амплитудно-частотных и фазо-частотных характеристик типовых динамических звеньев, построение по экспериментальным данным логарифмической амплитудной и фазовой характеристик, а также амплитудно-фазовой характеристики звена с проверкой значений экспериментальных и теоретических характеристик для данных частот.

3.1. краткие сведения из теории

Частотные характеристики систем (звеньев) заключают в себе полную информацию о динамических свойствах так же, как и дифференциальные уравнения и передаточные функции, которыми они описываются.

Частотные характеристики вытекают из комплексного коэффициента усиления W(jw) системы (звена), который может быть представлен в виде:

(3.1)

где A(w) = |W(jw)| – модуль комплексного коэффициента усиления;

j(w) – аргумент комплексного коэффициента усиления;

P(w) и Q(w) – действительная и мнимая части комплексного коэффициента усиления соответственно.

Изменение модуля и аргумента комплексного коэффициента усиления в функции частоты w, представленное в виде годографа на комплексной плоскости, называют амплитудно-фазовой характеристикой (рис. 3.1).

Модуль А(w) и аргумент j(w) комплексного коэффициента усиления как функции частоты представляют собой две частотные характеристики – амплитудно-частотная и фазо-частотная.

Действительная P(w) и Q(w) мнимая части комплексного коэффициента усиления представляют собой вещественную и мнимую частотные характеристики.

Каждая из этих характеристик может быть определена через другие частотные характеристики

;

; (3.2)

;

.

Рисунок 3.1. Фрагмент амплитудно-фазовой частотной характеристики.

Одним из достоинств применения частотных характеристик является возможность их экспериментального получения. Эксперимент заключается в следующем. На вход системы (звена) подается синусоидальный сигнал определенной частоты w (рис. 3.2):

.

Рисунок 3.2. К определению частотных характеристик.

Через некоторое время, необходимое для протекания переходного процесса (рис.3.2), элемент войдет в режим установившихся вынужденных колебаний. При этом, выходная величина y(t) будет изменятся по гармоническому закону с той же частотой w, но с отличающейся амплитудой Y_m и со сдвигом по оси времени (рис. 3.2):

,

(3.3)

φ - фазовый сдвиг между входным и выходным сигналами, градус.

Повторяя такой эксперимент при фиксированном X_m для различных значений частоты (от 0 до 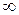), можно установить, что амплитуда Y_m и фазовый сдвиг φ выходного сигнала конкретного элемента зависят от частоты воздействия. Подавая гармоническое воздействие на вход различных элементов, можно убедиться, что величины Y_m и φ зависят также от типа и параметров элемента. Следовательно, зависимости амплитуды Y_m и сдвига фаз φ от значений частоты w могут служить характеристиками динамических свойств элементов. Так как амплитуда выходного сигнала Y_m зависит еще от амплитуды входного сигнала X_m, то целесообразно при описании передаточных свойств элементов рассматривать отношение амплитуд Y_m/X_m.

Зависимость отношения амплитуд выходного и входного сигнала от частоты называют амплитудной частотной характеристикой (АЧХ). Зависимость фазового сдвига между входным и выходным сигналами от частоты называют фазовой частотной характеристикой (ФЧХ).

В данной работе определяются частотные характеристики для апериодического, реального дифференцирующего и колебательного звеньев.

3.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Собрать схему получения частотных характеристик звеньев согласно рис. 3.3. В качестве исследуемого звена (блок W(p)) использовать модель апериодического звена с параметрами k = 0.7, T = 1.2 c. Амплитуду входного синусоидального сигнала установить равной единице: X_m = 1.

2. Изменяя частоту входного сигнала в заданных пределах измерить и занести в таблицу 3.1. значения амплитуды Y_m и сдвига по оси времени для каждого значения частоты. Измерения амплитуды Y_m и сдвига по оси времени выполняются после окончания переходного процесса - когда амплитуда выходного сигнала Y_m становится постоянной.

Рис. 3.3. Схема получения частотных характеристик динамических звеньев.

Таблица 3.1.

w, рад/с	0.1	0.3	0.5	0.7	0.9	1.0	1.5	2.0	2.5	3.0	3.5	5.0	7.0
, с
Ym
tмод, с

При выполнении моделирования необходимо для каждого диапазона частот задавать свое время моделирования t_мод (Stop time)- табл. 3.1.

3. Выполнить моделирование и получить частотные характеристики для реального дифференцирующего звена с параметрами k = 0.8, T = 0.6 c. Результаты занести в таблицу 3.1.

4. Выполнить моделирование и получить частотные характеристики для колебательного звена с параметрами k = 0.7, T = 0.5 c, ξ = 0.5. Результаты занести в таблицу 3.1

5. По полученным данным рассчитываются частотные характеристики A(w), j(w) - используя формулу (3.3), а также ; ; . Результаты занести в таблицу 3.2.

Таблица 3.2.

Замер	w, рад/с	A(w)	j(w)	P(w)	Q(w)	W(jw)

6. Построить экспериментальные частотные характеристики исследуемых звеньев: амплитудную частотную характеристику, фазовую частотную характеристику, действительную и мнимую частотные характеристики, амплитудно-фазовую частотную характеристику, логарифмические частотные характеристики.

7. Вывести соотношения для частотной характеристики каждого из исследуемых звеньев, взяв за основу выражения для их передаточных функций. Рассчитать и построить теоретические кривые амплитудно-частотной, фазочастотной, логарифмических амплитудной и фазовой характеристик, а также вещественной и мнимой на одних графиках с экспериментальными кривыми (результаты расчета свести в таблицу вида табл. 3.2). Сравнить их.

3.3.СОДЕРЖАНИЕ ОТЧЕТА

1. Краткое описание задачи и метода исследования.

2. Схема получения частотных характеристик.

3. Результаты эксперимента, сведенные в таблицу.

4. Результаты расчета по экспериментальным данным, сведенные в таблицу.

5. Выведенные соотношения для теоретического построения частотных характеристик.

6. Результата расчета по теоретическим данным, сведенные в таблицу.

7. Графики теоретических и экспериментальных кривых частотных характеристик.

8. Выводы о работе.