Однородные системы линейных уравнений
Однородная система линейных уравнений AX = 0 всегда совместна. Она имеет нетривиальные (ненулевые) решения, если r = rank A < n.
Для однородных систем базисные переменные (коэффициенты при которых образуют базисный минор) выражаются через свободные переменные соотношениями вида:
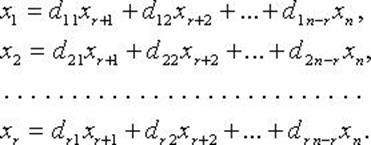
Тогда n - r линейно независимыми вектор-решениями будут:

а любое другое решение является их линейной комбинацией. Вектор-решения 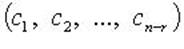 образуют нормированную фундаментальную систему.
образуют нормированную фундаментальную систему.
В линейном пространстве 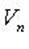 множество решений однородной системы линейных уравнений образует подпространство размерности n - r;
множество решений однородной системы линейных уравнений образует подпространство размерности n - r; 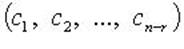 - базис этого подпространства.
- базис этого подпространства.
13 билет
ФУНДАМЕНТАЛЬНАЯ СИСТЕМА РЕШЕНИЙ
линейной однородной системы обыкновенных дифференциальных уравнений - базис векторного пространства действительных (комплексных) решений этой системы. (Система может состоять и из одного уравнения.) Более подробно это определение формулируется следующим образом.
Множество действительных (комплексных) решений {x1(t),...,xn(t)}(заданных на нек-ром множестве Е)линейной однородной системы обыкновенных дифференциальных уравнений наз. Ф. с. р. этой системы уравнений (на множестве Е)при выполнении совокупности следующих двух условий: 1) если действительные (комплексные) числа С 1,..., С n таковы, что функция C1x1(t)+...+Cnxn(t)тождественно равна нулю на Е, то все числа С 1,..., С n равны нулю; 2) для всякого действительного (комплексного) решения х(t)рассматриваемой системы уравнений найдутся действительные (соответственно комплексные) числа С 1,..., С n (не зависящие от t)такие, что x(t) = C1x1(t)+...+Cnxn(t)при всех 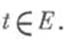
Если 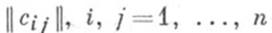 -произвольная невырожденная
-произвольная невырожденная 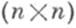 -матрица, а {x1(t), ..., х п(t)}есть Ф. с. р., то
-матрица, а {x1(t), ..., х п(t)}есть Ф. с. р., то 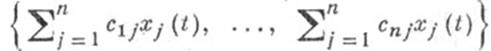 также есть Ф. с. р.; всякая Ф. <с. <р. получается таким преобразованием из данной Ф. с. р.
также есть Ф. с. р.; всякая Ф. <с. <р. получается таким преобразованием из данной Ф. с. р.
Если система дифференциальных уравнений имеет вид

где  (или
(или 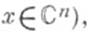 а
а 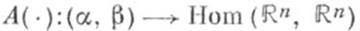 (соответственно
(соответственно 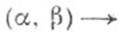
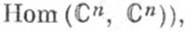 причем отображение
причем отображение 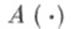 суммируемо на каждом отрезке, содержащемся в
суммируемо на каждом отрезке, содержащемся в 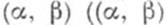 - конечный или бесконечный интервал в
- конечный или бесконечный интервал в 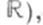 то векторное пространство решений этой системы изоморфно
то векторное пространство решений этой системы изоморфно 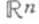 (соответственно
(соответственно 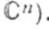 Следовательно, система (1) имеет бесконечно много Ф. с. р., и каждая такая Ф. с. р. состоит из пре шений. Напр., для системы уравнений
Следовательно, система (1) имеет бесконечно много Ф. с. р., и каждая такая Ф. с. р. состоит из пре шений. Напр., для системы уравнений
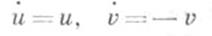 произвольная Ф. с. р. имеет вид
произвольная Ф. с. р. имеет вид
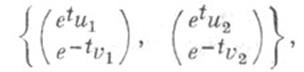
где 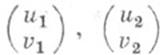 -произвольные линейно независимые векторы-столбцы.
-произвольные линейно независимые векторы-столбцы.
Всякая Ф. с. р. системы (1) имеет вид
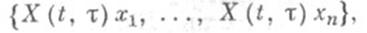
где 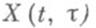 - Коши оператор системы (1),
- Коши оператор системы (1), 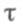 - произвольное фиксированное число из интервала
- произвольное фиксированное число из интервала 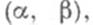 а x1, . . ., х п - произвольный фиксированный базис пространства
а x1, . . ., х п - произвольный фиксированный базис пространства 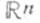 (соответственно
(соответственно 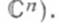
Если система дифференциальных уравнений состоит из одного уравнения
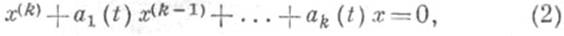
где функции
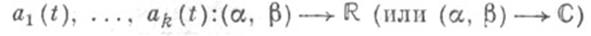 суммируемы на каждом отрезке, содержащемся в
суммируемы на каждом отрезке, содержащемся в 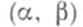 (где
(где 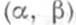 - конечный или бесконечный интервал в
- конечный или бесконечный интервал в 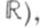 то векторное пространство решений этого уравнения изоморфно
то векторное пространство решений этого уравнения изоморфно 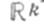 (соответственно
(соответственно 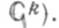 Следовательно, уравнение (2) имеет бесконечно много Ф. с. р., и каждая из них состоит из kрешений. Напр., уравнение
Следовательно, уравнение (2) имеет бесконечно много Ф. с. р., и каждая из них состоит из kрешений. Напр., уравнение 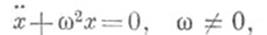 имеет Ф. с. р.
имеет Ф. с. р.  общее действительное решение этого уравнения дается формулой
общее действительное решение этого уравнения дается формулой 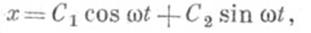 где C1, С2 - произвольные действительные постоянные.
где C1, С2 - произвольные действительные постоянные.
Если система дифференциальных уравнений имеет вид
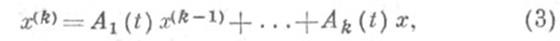
где  (или
(или 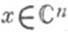 ) и при всяком i = l, ..., k-1 отображение
) и при всяком i = l, ..., k-1 отображение
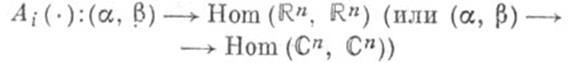
суммируемо на каждом отрезке, содержащемся в 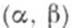 (где
(где 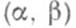 -конечный или бесконечный интервал в
-конечный или бесконечный интервал в 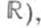 то пространство решений этой системы уравнений изоморфно
то пространство решений этой системы уравнений изоморфно 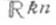 (соответственно
(соответственно 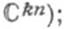 Ф. с. р. системы (3) существуют, и каждая из них состоит из kn решений.
Ф. с. р. системы (3) существуют, и каждая из них состоит из kn решений.
Для линейных однородных систем дифференциальных уравнений, не разрешенных относительно старших производных, даже если коэффициенты системы постоянные, число решений, входящих в Ф. с. р. (т. е. размерность векторного пространства решений), вычисляется иногда не столь просто, как в вышеприведенных случаях. (В [1], з 11 рассмотрено такое вычисление для линейных систем дифференциальных уравнений с постоянными коэффициентами, не разрешенных относительно старших производных.)
14 билет
Векторы на плоскости
Определение вектора
Рассмотрим на плоскости две точки A и B. Обозначим через 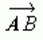 вектор AB, понимая под этим направленный отрезок AB, т. е. отрезок, у которого точка A является началом, а точка B -- концом . Таким образом, точки A и B, ограничивающие вектор вектор AB, понимая под этим направленный отрезок AB, т. е. отрезок, у которого точка A является началом, а точка B -- концом . Таким образом, точки A и B, ограничивающие вектор 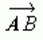 , играют различную роль. Именно в этом в первую очередь и состоит главное различие между вектором , играют различную роль. Именно в этом в первую очередь и состоит главное различие между вектором 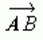 и отрезком AB. Две точки A и B плоскости задают два различных вектора и отрезком AB. Две точки A и B плоскости задают два различных вектора 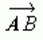 и и 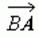 одинаковой длины и противоположно направленные. одинаковой длины и противоположно направленные. |
Сложение векторов


Параллельный перенос
Под параллельным переносом вдоль вектора понимают перемещение всех точек пространства в одном направлении на одинаковое расстояние. Определим сложение векторов так, чтобы последовательные сдвиги вдоль двух векторов соответствовали сдвигу вдоль суммы этих векторов.
Пусть даны два вектора 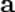 и
и 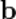 . Приложим вектор
. Приложим вектор 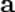 к некоторой точке
к некоторой точке  , получим
, получим 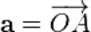 . Приложим вектор
. Приложим вектор 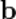 к точке
к точке 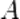 , получим
, получим 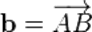 . Тогда вектор
. Тогда вектор 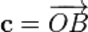 будем называть суммой векторов:
будем называть суммой векторов: 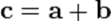 .
.

Докажем, что данное определение не зависит от выбора точки  .
.
Приложим вектор 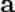 к другой точке
к другой точке 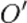 , получим
, получим 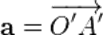 . Приложим вектор
. Приложим вектор 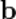 к точке
к точке 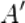 , получим
, получим 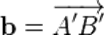 .
.
Рассмотрим направленные отрезки 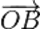 и
и 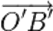 . Они, очевидно, равны (см. рис.), поскольку
. Они, очевидно, равны (см. рис.), поскольку 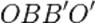 — параллелограмм.
— параллелограмм.
Умножение на число
Произведением вектора 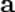 на число
на число 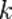 называется вектор, который:
называется вектор, который:
- коллинеарен вектору
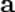 ;
; - сонаправлен ему, если
 , или противоположнонаправлен, если
, или противоположнонаправлен, если  ;
; - длины связаны следующим соотношением:
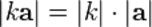 .
.
Данное определение согласовано с определением сложения:
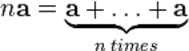 |
для любого натурального 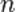 .
.
