Свойства дифференциала
Если 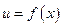 и
и 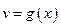 - функции, дифференцируемые в точке
- функции, дифференцируемые в точке  , то непосредственно из определения дифференциала следуют следующие равенства:
, то непосредственно из определения дифференциала следуют следующие равенства:
1) 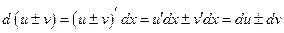
2) 
3) 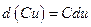
4) 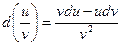
Дифференциал сложной функции.
Инвариантная форма записи дифференциала
Пусть 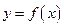 ,
, 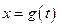 , т.е
, т.е 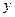 - сложная функция. Тогда
- сложная функция. Тогда
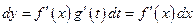 .
.
Следовательно, форма записи дифференциала 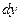 не зависит от того, является ли
не зависит от того, является ли  независимой переменной или функцией какой-либо другой переменной, в связи с чем эта форма записи называется инвариантной формой записи дифференциала.
независимой переменной или функцией какой-либо другой переменной, в связи с чем эта форма записи называется инвариантной формой записи дифференциала.
Однако, если  - независимая переменная, то
- независимая переменная, то 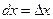 , но
, но
если  зависит от t, то
зависит от t, то 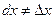 .
.
Пример. Найти производную функции 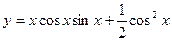 .
.
Сначала преобразуем данную функцию: 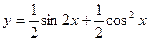 . Тогда
. Тогда
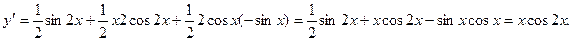
Пример. Найти производную функции 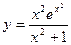 . Имеем
. Имеем
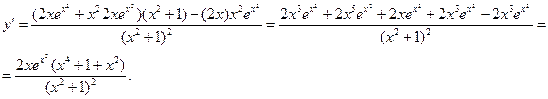
Пример. Найти производную функции 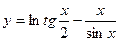 . Имеем
. Имеем
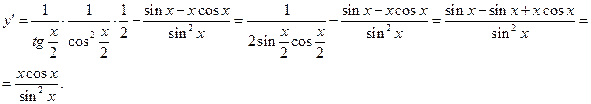
Пример. Найти производную функции 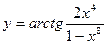 . Имеем
. Имеем
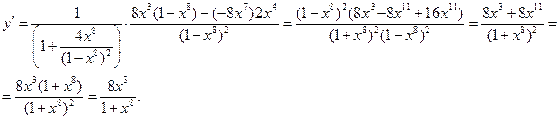
Пример. Найти производную функции 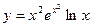 . Имеем
. Имеем
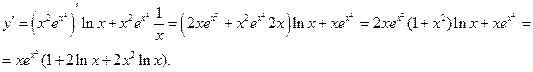
Формула Тейлора
Теорема Тейлора. 1) Пусть функция  имеет в точке
имеет в точке 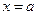 и некоторой ее окрестности производные порядка до
и некоторой ее окрестности производные порядка до 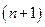 включительно, (т.е. все предыдущие до порядка n функции и их производные непрерывны и дифференцируемы в этой окрестности).
включительно, (т.е. все предыдущие до порядка n функции и их производные непрерывны и дифференцируемы в этой окрестности).
2) Пусть х- любое значение из этой окрестности, причём 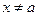 .
.
Тогда между точками х и а найдется такая точка 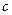 , что справедлива формула:
, что справедлива формула:
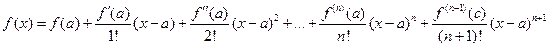
- это выражение называется формулой Тейлора, а выражение:
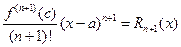
называется остаточным членом в форме Лагранжа.
Доказательство. Представим функцию  в виде некоторого многочлена
в виде некоторого многочлена 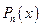 , значение которого в точке
, значение которого в точке 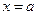 равно значению функции
равно значению функции  , а значения его производных равно значениям соответствующих производных функции в точке
, а значения его производных равно значениям соответствующих производных функции в точке 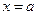 :
:
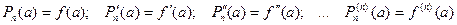 .
.
Чем больше значение 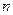 , тем ближе значения многочлена к значениям функции, тем точнее он определяет функцию.
, тем ближе значения многочлена к значениям функции, тем точнее он определяет функцию.
Представим этот многочлен с неопределенными пока коэффициентами:
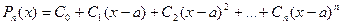 .
.
Для нахождения неопределенных коэффициентов вычисляем производные многочлена в точке 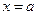 и составляем систему уравнений:
и составляем систему уравнений:
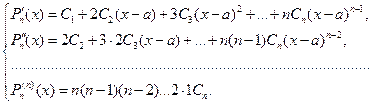
Решение этой системы при 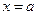 не вызывает затруднений, получаем:
не вызывает затруднений, получаем:
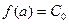 ,
,
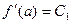 ,
,
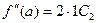 ,
,
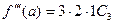 ,
,
…………………….
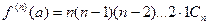 .
.
Подставляя полученные значения 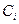 в формулу (
в формулу (  ), получи:
), получи:
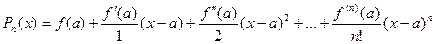 .
.
Как было замечено выше, многочлен не точно совпадает с функцией  , т.е. отличается от нее на некоторую величину. Обозначим эту величину
, т.е. отличается от нее на некоторую величину. Обозначим эту величину 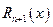 .
.
Тогда:
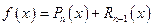 .
.
Теорема доказана.
Иногда используется другая запись для остаточного члена 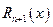 . Тавк как точка
. Тавк как точка 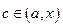 , то найдется такое число q из интервала
, то найдется такое число q из интервала 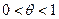 , что
, что 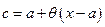 . Тогда можно записать:
. Тогда можно записать:
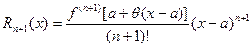
Тогда, если принять 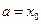 ,
, 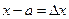 ,
, 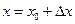 , формулу Тейлора можно записать в виде:
, формулу Тейлора можно записать в виде:
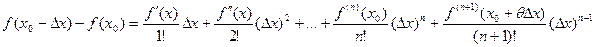
где 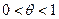 . Если принять
. Если принять 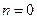 , получим:
, получим:
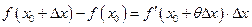 .
.
Формула Тейлора имеет огромное значение для различных математических преобразований. С ее помощью можно находить значения различных функций, интегрировать, решать дифференциальные уравнения и т.д.
Формула Маклорена
Формулой Маклоренаназывается формула Тейлора при 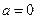 :
:
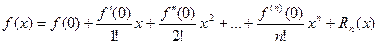
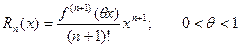
Следует отметить, что при разложении функции в ряд применение формулы Маклорена предпочтительнее, чем применение непосредственно формулы Тейлора, т.к. вычисление значений производных в нуле проще, чем в какой- либо другой точке, естественно, при условии, что эти производные существуют.
Однако, выбор числа а очень важен для практического использования. Дело в том, что при вычислении значения функции в точке, расположенной относительно близко к точке а, значение, полученное по формуле Тейлора, даже при ограничении тремя – четырьмя первыми слагаемыми, совпадает с точным значением функции практически абсолютно. При удалении же рассматриваемой точки от точки а для получения точного значения надо брать все большее количество слагаемых формулы Тейлора, что неудобно.
Другими словами, чем больше по модулю значение разности 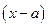 тем более точное значение функции отличается от найденного по формуле Тейлора.
тем более точное значение функции отличается от найденного по формуле Тейлора.
Кроме того, можно показать, что остаточный член 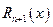 является бесконечно малой функцией при
является бесконечно малой функцией при 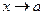 , причем долее высокого порядка, чем
, причем долее высокого порядка, чем 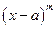 , т.е.
, т.е.
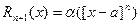 .
.
Таким образом, ряд Маклорена можно считать частным случаем ряда Тейлора.
