Разложение данной функции в ряд Тейлора приведет к выражению
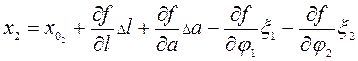 (83)
(83)
Полагая x2 безошибочным это выражение переписывают так
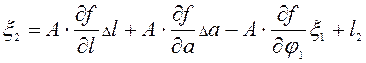 (84)
(84)
Где
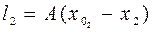 (85)
(85)
a 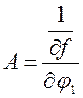 (86)
(86)
Для пункта с номером i можно записать
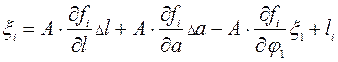 (87)
(87)
Для решения поставленной задачи все пункты располагают вдоль меридиана (рис.)

 i Таким образом составляется система уравнений поправок с тремя 3 неизвестными Dl, Da, x1.
i Таким образом составляется система уравнений поправок с тремя 3 неизвестными Dl, Da, x1.
2 
 Теперь необходимо составить соответствующую систему по дуге
Теперь необходимо составить соответствующую систему по дуге
1 параллели. Формула длины параллели имеет вид
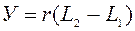 (88)
(88)
Где r – радиус параллели, вычисляемый по формуле
РИС. 8 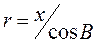 (89)
(89)
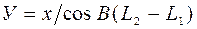 (90)
(90)
Принцип составления соответствующего уравнения относительно Dl, Da здесь такой же, как и в предыдущем случае.
Поскольку из астрономических определений находят долготу l то можно записать
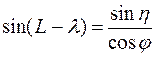 (91)
(91)
Очевидно, что
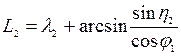 (92)
(92)
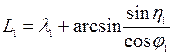 (93)
(93)
Подставляя эти выражения в формулу вычисления длины дуги параллели последнюю в общем виде запишем так
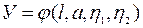 (94)
(94)
Разложение её в ряд Тейлора при приближенных значениях l и a приводим к выражению
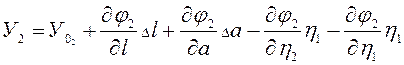 (95)
(95)
Что соответствует следующему линейному уравнению
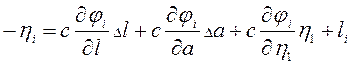 (96)
(96)
Где
 (97)
(97)
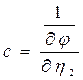 (98)
(98)
В данном случае пункты располагают вдоль параллели. Значения Dl, Da, x1, и h1 находят по методу наименьших квадратов, полагая
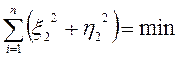 (99)
(99)
Уравнения для первого пункта имеет вид
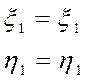 (100,101)
(100,101)
· Способ площадей.
В этом способе используется сеть геодезических пунктов, на которых определяются астрономические широты ji и долготы li.
Пусть известны значения широт и долгот при приближенных значениях параметров эллипсоида: а0, l0. Обозначим их через dBi° и dL i° .
Тогда можно записать, что на определяемом эллипсоиде должны быть справедливыми следующие уравнения.
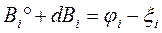 (102)
(102)
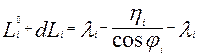 (103)
(103)
Или
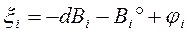 (104)
(104)
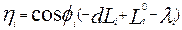 (105)
(105)
Значения dBi и dLi по правила сферической геодезии выражают через dB1, dL1, dA1, Da, Dl, где dB1, dL1 – поправки в координаты исходного пункта эллипсоида, dA1 – поправка в длину с исходного пункта на текущий.
В свою очередь для исходного пункта эллипсоида можно записать
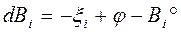 (106)
(106)
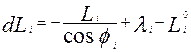 (107)
(107)
С углом этих выражений получают линейные уравнения для xi и hi в функции от Da, Dl, xi , hi, которые решаются по методу наименьших квадратов при условии
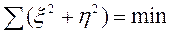 (108)
(108)
· Способ проектирования.
В этом случае также составляется система уравнений
 (109,110)
(109,110)
Для каждого пункта астрономической сети. Кроме того для каждого из них добавляется следующее уравнение
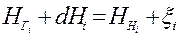 (111)
(111)
Где Hг, Hн – геодезическая высота точки и высота точки над уровнем моря (геоидом) соответственно, xi – высота геоида над эллипсоидом, dHi – поправка в геодезическую высоту за переход к новому эллипсоиду.
Как и в способе площадей dBi, dLi выражают через xi, hi.
Далее предполагается, что геоцентрические координаты точек получают одинаковое смещение.В этой связи dBi, dLi выражают через dx, dу, dz. Таким образом неизвестными в данной задаче будут dx, dу, dz, Da, Dl.
Полученную систему уравнений тоже решают по методу наименьших квадратов при условии
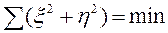 (112)
(112)
Глава 4.
Система высот.
Согласно теории Стокса для определения высоты точки земной поверхности относительно эллипсоида ещё необходимо знать высоту этой точки относительно геоида. Высоты обычно получают из геометрического нивелирования. Полагаем, что из-за неоднородности гравитационного поля высоты точек определяются неоднозначно. Пусть имеется некоторая исходная уровенная плоскость (рис.)
 |  |  |

 d
d


 c
c
 |

 bBn
bBn



 ah
ah
A1A2
РИС.9
На ней точки A1 и A2 находятся на одинаковой высоте над уровнем моря. Обозначим через h2 – превышение точки B над точками A1 и A2 . Линии c и d – уровенные поверхности гравитационного поля.
При нивелировании между точками A и B расположен нивелир на уровенной поверхности l. В таком положении пузырёк уровня будет находится в нуль пункте, но визирная ось трубы находясь в плоскости уровенной поверхности l не будет горизонтальной исходной уровенной поверхности точек A1 и A2. В результате разность отсчётов a - b не будет равна превышению h. Эта же уровенная поверхность на участке BA2 паралельна исходной поверхности и разность отсчётов m - n равна превышению h между точками A2 и В.
Как видим, из-за не параллельности уровенных поверхностей получаются различные значения превышений между одними и теми же точками. С тем, чтобы ликвидировать такое различие необходимо вводить поправки за не параллельность уровенной поверхности. А это требует введения определенной системы высоты, построенной на основе теории потенциала.
