Теоретические сведения. Теория вероятностей

Теория вероятностей

Методические указания

к практическим занятиям по дисциплине

«Теория вероятностей,

математическая статистика и случайные процессы»

для студентов специальности 220400

Саратов 2004

Тема 1. Элементы комбинаторики

Теоретические сведения

При выборе m элементов из n различных элементов говорят, что они образуют соединение из n элементов по m. Различают три вида соединений элементов:

1. Размещениями называются соединения, которые отличаются друг от друга составом элементов или их порядком, и каждое из которых содержит m элементов, взятых из n различных элементов.

Например, выпишем все размещения элементов a, b, c, d по два: ab, ba, ac, ca, ad, da, bc, cb, bd, db, cd, dc.

2. Перестановками из n элементов называются соединения, каждое из которых содержит n различных элементов, взятых в определенном порядке.

Например, выпишем все перестановки из элементов a, b, c: abc, acb, bac, bca, cab, cba.

3. Сочетаниями из n элементов по m называются соединения, отличающиеся друг от друга, по крайней мере, одним элементом, каждое из которых содержит m элементов, взятых из n различных элементов.

Например, выпишем все сочетания из элементов a, b, c, d, e по три: abc, abd, abe, acd, ace, ade, bcd, bce, bde, cde.

Задача о числе размещений:Сколькими способами можно выбрать и разместить по m различным местам n разных предметов? Количество таких способов обозначается 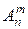и читается: «число размещений из n по m».

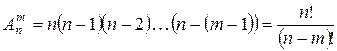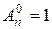, (по определению)

Пример 1. Сколько всего пятизначных телефонных номеров, в каждом из которых ни одна цифра не повторяется?

Решение. Это задача о выборе и размещении по пяти разным местам пяти из десяти различных цифр. Поэтому число указанных телефонных номеров равно .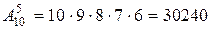

Пример 2. Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные?

Решение. Поскольку нечетных цифр пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на две разные позиции двух из пяти различных цифр. Следовательно, указанных чисел имеется .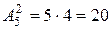

Задача о числе перестановок:Сколькими способами можно переставить n разных предметов, расположенных на n разных местах? Количество таких способов обозначается 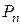и читается: «число перестановок из n».

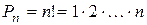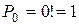, (по определению)

Пример 1. Сколько всего шестизначных четных чисел можно составить из цифр 1, 3, 4, 5, 7, 9, если в каждом из этих чисел ни одна цифра не повторяется?

Решение. Из всех указанных цифр последней может быть только цифра 4. Остальные пять цифр могут стоять на оставшихся пяти местах в любом порядке. Значит, нужно найти число перестановок из пяти элементов. 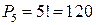. Таким образом, можно составить 120 указанных чисел.

Пример 2. Сколькими способами семь книг разных авторов можно поставить на полке в один ряд?

Решение. Эта задача о числе перестановок семи разных книг 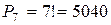. Следовательно, имеется 5040 способов осуществить расстановку книг.

Задача о числе сочетаний:Сколькими способами можно выбрать m из n разных предметов? Количество таких способов обозначается 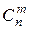и читается: «число сочетаний из n по m».

; ; .

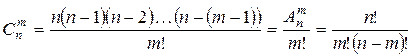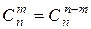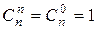Пример1. Сколькими способами читатель может выбрать две книжки из пяти имеющихся?

Решение. Искомое число способов равно числу сочетаний из пяти по два. Так как 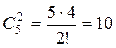, то указанную выборку читатель может осуществить десятью способами.

Пример 2. В выпуклом семиугольнике проведены всевозможные диагонали, при этом никакие три из них не пересекаются в одной точке. Сколько точек пересечения указанных диагоналей?

Решение. Каждой точке пересечения диагоналей соответствуют четыре вершины семиугольника, а каждой четверке вершин семиугольника соответствует одна точка пересечения. Поэтому число всех точек пересечения диагоналей равно числу способов, которыми среди семи вершин можно выбрать четыре вершины. Поскольку 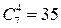, то число точек пересечения диагоналей равно 35.

Правило сложения

Если некоторый предмет 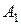может быть выбран из совокупности предметов 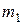способами, а другой предмет 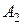может быть выбран 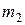способами, то выбрать либо 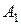, либ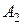о можно 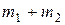способами. Правило распространяется на совокупность .

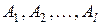Правило умножения

Если некоторый предмет 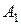можно выбран из совокупности предметов 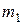способами и после каждого такого выбора предмет 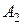может быть выбран 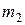способами, то пара объектов ( 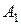, 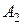) в указанном порядке может быть выбрана 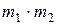способами. Правило распространяется на совокупность .

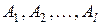Пример 1. Из двух математиков и десяти экономистов надо составить комиссию в составе восьми человек. Сколькими способами может быть составлена комиссия, если в нее должен входить хотя бы один математик?

Решение. В указанной комиссии может быть либо один математик и семь экономистов, либо два математика и шесть экономистов. Выбор одного математика из двух возможен 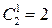способами, а семи экономистов из десяти – 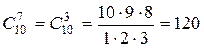способами. По правилу произведения число способов выбора комиссии из одного математика и семи экономистов равно 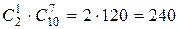. Выбор двух математиков из двух возможен 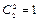способом, а шести экономистов из десяти – 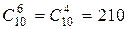способами. По правилу произведения число способов выбора комиссии из двух математиков и семи экономистов равно 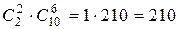. Общее число способов выбора комиссии с одним или с двумя математиками по правилу сложения равно .

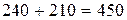Пример 2. Сколько существует делителей числа 210?

Решение. Разложим данное число на простые множители: 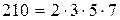. Число делителей, составленных из произведения двух простых множителей, равно 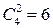(это числа 6, 10, 14, 15, 21, 35); число делителей, составленных из произведения трех простых множителей, равно 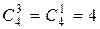(это числа 30, 42, 70, 105); число простых делителей равно четырем (это числа 2, 3, 5, 7). Кроме того, делителями являются число 1 и число 210. Итак, согласно правилу сложения, число всех делителей равно .

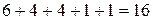До сих пор рассматривались соединения, в каждое из которых любой из n различных элементов входит один раз. Можно рассматривать соединения с повторениями.

Размещения с повторениями. Например, выпишем размещения по три из элементов 4 и 5 с повторениями: 444, 445, 454, 544, 555, 554, 545, 455.

Задача о числе размещений с повторениями: Сколькими способами можно разместить по m различным местам любые m предметов, выбранных из n различных предметов с повторениями каждого из них любое число раз, но не более m?

.

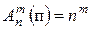Пример 1. Каждый телефонный номер состоит из 5 цифр. Сколько всего телефонных номеров, содержащих только цифры 2, 3, 5 и 7?

Решение. Это задача о числе размещений в пяти разных местах пяти цифр, выбранных из четырех разных цифр с повторениями каждой из них любое число раз, но не более пяти. Так как 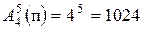, то число всех указанных телефонных номеров равно 1024.

Пример 2. Буквы азбуки Морзе состоят из символов – точка и тире. Сколько букв получим, если потребуем, чтобы каждая буква состояла не более чем из пяти указанных символов?

Решение. Число всех букв, каждая из которых записывается одним символом, равно 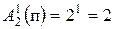. Число всех букв, каждая из которых записывается двумя символами, равно 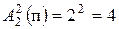. Число всех букв, каждая из которых записывается тремя символами, равно 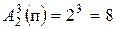. Число всех букв, каждая из которых записывается четырьмя символами, равно 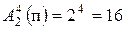. Число всех букв, каждая из которых записывается пятью символами, равно 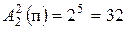. Число всех указанных букв равно 62.

Перестановки с повторениями – перестановки из n предметов, в каждую из которых входят 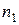одинаковых предметов одного типа, 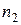одинаковых предметов другого типа и т.д. 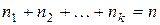. Например, выпишем перестановки с повторениями цифр 4 и 5, каждая из которых взята по два раза: 4455, 5544, 4545, 5454, 4554, 5445.

Задача о числе перестановок с повторениями: Сколькими способами можно переставить n предметов k различных типов каждого типа соответственно 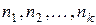одинаковых предметов, расположенных на n разных местах?

.

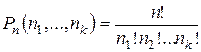Пример 1. Сколькими способами можно расположить в ряд 2 зеленые и 4 красные лампочки?

Решение. 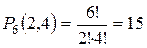способами.

Пример 2. Сколькими способами можно переставить буквы в слове какао, чтобы получались всевозможные различные наборы букв?

Решение. 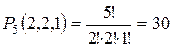способами.

Сочетания с повторениями. Например, выпишем все сочетания из трех цифр 3, 4,5 по два с повторениями: 33, 34 (43), 35 (53), 44, 45 (54), 55.

Задача о числе сочетаний с повторениями: Если имеется по m одинаковых предметов каждого из n различных типов, то сколькими способами можно выбрать m из этих m×n предметов?

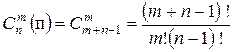
Пример 1. В кондитерской имеется пять разных сортов пирожных. Сколькими способами можно выбрать набор из четырех пирожных?

Решение. 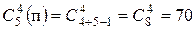способов.

Пример 2. Сколькими способами можно выбрать четыре монеты из четырех пятирублевых и из четырех двухрублевых монет?

Решение. 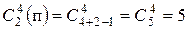способов.

Упражнения

1) Сколько можно составить сигналов из 6 флагов разного цвета, взятых по 2?

2) Сколькими способами можно из 20 студентов группы выбрать старосту и профорга?

3) Сколькими способами можно разложить 8 разных писем по 8 разным конвертам, если в каждый конверт кладется только одно письмо?

4) 12 человек играют в городки. Сколькими способами они могут набрать команду из четырех человек на соревнования?

5) В розыгрыше первенства по футболу принимают участие 16 команд, при этом любые две команды играют между собой только один матч. Сколько всего игр?

6) Сколькими способами можно разместить восемь пассажиров в три вагона?

7) Сколько будет костей домино, если использовать в их образовании все цифры?

8) Десять книг (7 книг различных авторов и трехтомник одного автора) помещены на книжной полке. Сколькими способами их можно расставить на полке так, чтобы книги автора трехтомника стояли рядом?

9) Сколькими способами можно рассадить на скамейке пять человек?

10) Сколько всего четырехзначных чисел, делящихся на 2?

11) В подразделении 30 солдат и три офицера. Сколькими способами можно выделить патруль, состоящий из трех солдат и одного офицера?

12) Сколькими способами можно разделить группу из 15 человек на две группы так, чтобы в одной было 4 человека, а в другой 11?