В задаче предполагается, что проведен некоторый эксперимент, в результате которого получен набор данных
Найти указанные пределы
а) 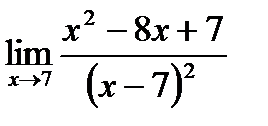 ; б)
; б) 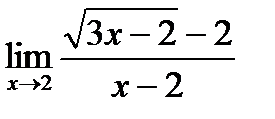 ;
;
в) 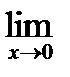
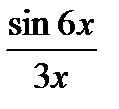 ; г)
; г) 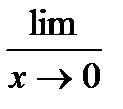
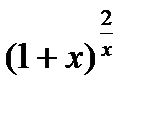 ;
;
Найти производные функций
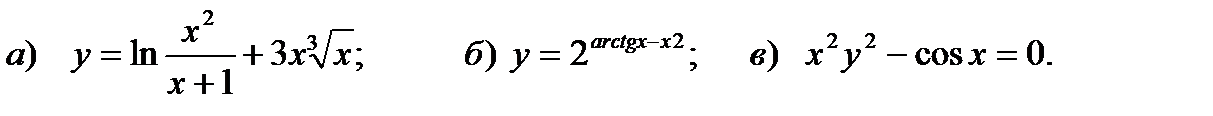
Провести полное исследование функции и построить её график
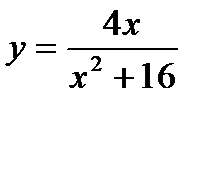 ;
;
Решить средствами дифференциального исчисления
Сечение тоннеля имеет форму прямоугольника, завершённого сверху полукругом. Периметр сечения 18 м. При каком радиусе полукруга площадь сечения будет наибольшей?
Решить указанные неопределенные интегралы и результаты интегрирования проверить дифференцированием
а) 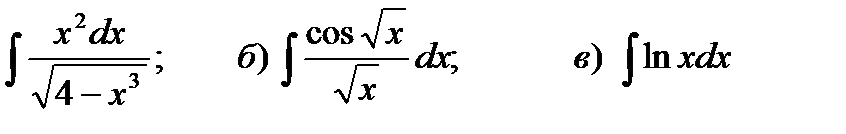 .
.
6. вычислить площадь фигуры, ограниченной указанными линиями. Сделать чертеж:
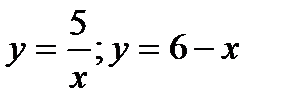 .
.
Найти общее решение дифференциальных уравнений первого порядка.
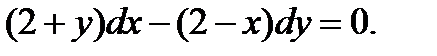
Найти общее решение линейного дифференциальных уравнений первого порядка.
72. 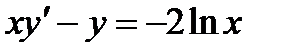 .
.
Найдите частное решение линейного дифференциального уравнения второго порядка, удовлетворяющие указанным начальным условиям
82. 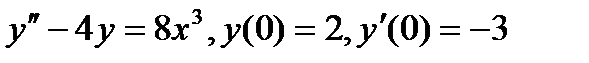 .
.
Решить, применяя теоремы сложения и умножения вероятностей.
Из трех орудий произвели залп по цели. Вероятность попадания в цель при одном выстреле из первого орудия равна 0,8; для второго и третьего орудия эти вероятности соответственно равны 0,6 и 0,9. Найти вероятность того, что: 1) только один снаряд поразит цель; 2) только два снаряда поразят цель; 3) все три снаряда поразят цель.
Решить, применяя формулу полной вероятности или Байеса.
При проверке качества зерен пшеницы было установлено, что все зерна могут быть разделены на 4 группы. К зернам 1-й группы принадлежит 96%, ко второй 2%, к 3-й 1%, к 4-й 1% всех зерен. Вероятность того, что из зерна вырастет колос, содержащий не менее 50 зерен для 1-й группы равна 0,5; 2-й группы 0,2; 3-й группы 0,18; 4-й группы 0,02. Найти вероятность того, что из взятого наугад зерна вырастет колос, содержащий не менее 50 зерен.
Составить ряд, функцию распределения для рассматриваемой ДСВ. Найти числовые характеристики.
В партии из шести деталей имеется 4 стандартных. Наудачу отобраны 3 детали. Составить ряд и функцию распределения числа стандартных деталей среди отобранных. Найти числовые характеристики. Вычислить вероятность того, что число стандартных деталей не меньше двух.
В задаче предполагается, что проведен некоторый эксперимент, в результате которого получен набор данных.
Требуется:
1. Построить вариационный ряд частот или относительных частот;
2. Изобразить геометрически вариационный ряд, построив гистограмму частот;
3. Вычислить точечные оценки параметров распределения;
4. Высказать гипотезу о виде закона распределения признака и применить критерий согласия хи-квадрат Пирсона на 5%-м уровне значимости;
5. Считая полученный набор данных генеральной совокупностью, сделать из этой совокупности выборку объема 10, для которой:
а) вычислить точечные оценки параметров распределения – выборочную среднюю арифметическую 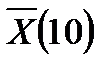 и исправленную выборочную дисперсию
и исправленную выборочную дисперсию 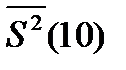 , сравнить полученные значения с соответствующими характеристиками генеральной совокупности;
, сравнить полученные значения с соответствующими характеристиками генеральной совокупности;
б) найти доверительный интервал для генеральной средней на уровне значимости 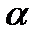 =0,05 при неизвестной и известной дисперсии;
=0,05 при неизвестной и известной дисперсии;
в) найти доверительный интервал для генеральной дисперсии.
Выработка продукции предприятиями в сравнении с предыдущей пятилеткой дается таблицей (в %):
