Имитация сложного события, состоящего из зависимых событий

В случае, когда сложное событие состоит из элементарных зависимых событий А и В имитация сложного события производится с помощью проверки следующих неравенств:

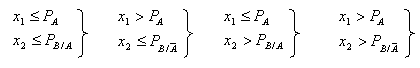
В зависимости от того, какая из этих четырех систем неравенств выполняется, делается вывод о том, какой из этих четырех возможных исходов 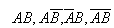имеет место.

В качестве исходных данных задаются 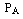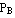_, и условная вероятность 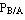, вероятность 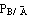может быть вычислена. По формуле полной вероятности: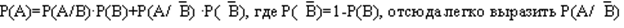

Имитация событий, составляющих полную группу

Пусть событие А_i (i=1,n) составляют полную группу, тогда их вероятности Р_i, таковы что:

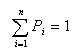
Имитация факта появления одного из событий А_i (i=1,n) сводится к проверке следующих неравенств:

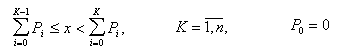
Выполнение К-го неравенства эквивалентно выполнению события А_К. Описанный алгоритм называют иногда алгоритмом “розыгрыша по жребию”. Его можно интерпретировать как установление номера К-го отрезка длинной Р_К, на который пало СЧ х, при условии разбиения отрезка единичной длины на отрезки с длинами P1,P2,...Pn (рис 3.3.)

Рис. 3.3.

Вопросы для самопроверки

1. Как Вы понимаете смысл слов “имитация факта наступления события” и “имитация события”? В данном тексте это одно и тоже?

2. Докажите, что алгоритмы имитации сложных событий (параграфы 2.8. и 2.9.) могут быть сведены к имитации полной группы событий, сравните их. Какие алгоритмы предпочтительнее?

3. Докажите справедливость алгоритмов, описанных в параграфе 2.8.

Упражнения

1. Проектируемый объект состоит из трех независимых узлов. Вероятности безотказной работы каждого узла: Р₁=0,9; Р₂=0,85; Р₃=0,8. В процессе проектирования проводится 10³ имитационных экспериментов (ИЭ) над математической моделью (ММ) объекта. Составить программу и блок-схему для подсчета количества возможных исходов.

2. Проектируемый объект состоит из двух блоков, вероятности отказов которых Р₁=0,1 и Р₂=0,15. Если вышел из строя второй блок, то вероятность отказа первого увеличивается до Р₁=0,15. Над ММ объекта проводится ИЭ. Составить блок-схему алгоритма и программу, позволяющего оценить вероятности всевозможных вариантов отказов, если количество ИЭ равно 10².

3. Вероятность появления сбоя при работе информационной системы в течение часа равна 0,1. Если количество сбоев произошло 3 раза подряд, то состояние системы оценивается как “аварийное”. Оценить вероятность наступления аварийной ситуации в течении 30 дней (рабочий день 8 часов).

4. Вычислительный комплекс имеет 3 процессора. В случае максимальной загрузки задачи простаивают в очереди на выполнение 0,5 мин. (нормальный режим.) Составить блок-схему и программу имитации возможных режимов работы комплекса, подсчитать количество случаев ненормальной работы, если вероятность отказа каждого процессора равна 0,1 , а количество проводимых ИЭ – .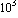

5. С помощью ИЭ приводится сравнение двух технологий изготовления изделий. В первом случае изделие проходит пять технологических операций, вероятности появления брака при каждой из которых независимы и равны соответственно P1,P2,P3,P4,P5, вторая технология содержит семь операций с вероятностями брака Р6, Р7, Р8, Р9,Р10,Р11,Р12. Составить блок-схему алгоритма и программу оценки технологий по количеству производимого брака. Предположить, что изготовлению подлежат n изделий (n=100).

6. Изделие изготавливается с вероятностью Р₁ – неустранимого брака и Р₂ – устранимого брака. Начертить блок-схему и составить программу имитации процесса изготовления N изделий, предусмотреть вычисление оценки вероятности изготовления детали без брака (n=100).

7. Оценить надежность изделия, состоящего из трех узлов и устройств А, B, C, D,E, F (РИС. 3.4.). Узел 1 выходит из строя, когда выходят из строя А и В. Узел 2 не исправен, когда вышло из строя С. Узел 3 выходит из строя, когда одновременно вышли из строя D, E, F. Вероятности безотказной работы всех устройств равны соответственно: Р(А)=0,8; Р(В)=0,7; Р(С)=0,95; Р(D)=0,85; P(E) =0,9; P(F)=0,7. Составить блок-схему и программу для получения оценки вероятности безотказной работы всей системы, количество НЭ взять равным 100. Можно ли решить задачу аналитическими методами? В каких случаях задачу следует решать методами имитационного моделирования? Если возможно решение задачи аналитически, то сравните полученные разными способами решения.

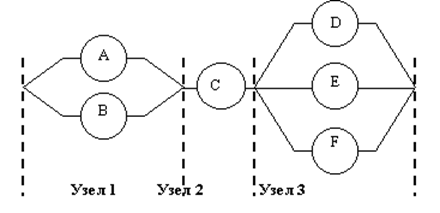
Рис. 3.4.