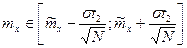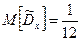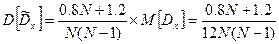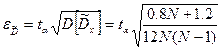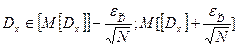Характеристики рассеивания случайной величины
Различают моменты: начальные и центральные.
Начальным моментом k-го порядка называют:
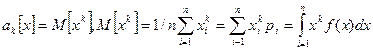
Центральным моментом k-го порядка называют:
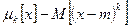
Вычисляется:
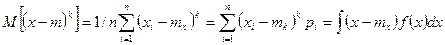
Свойства центрального момента:
1о. М1[х]=0
2о. М2[х] – дисперсия случайной величины.
Центральный момент третьего порядка служит для определения характеристик асимметрии распределения случайной величины относительно его математического ожидания.
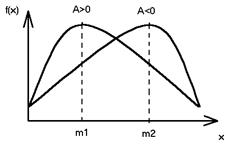
Коэффициент симметрии: 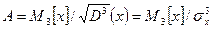
Если значение А>0, то функция плотности распределения смещена влево, если значение A<0, то функция плотности распределения смещена вправо относительно М0.
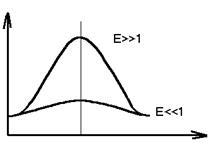
М4[x] служит для определения крутизны для распределения случайной величины.
Коэффициент эксцесса:
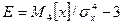
Характеризует крутизну распределения относительно нормального закона распределения, для которого указанная величина равна 3.
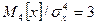
 |
Характеристика вероятностных взаимодействий решает следующую задачу:
Дано две случайные величины: X; Y. Определить их зависимость и независимость.
Корреляционный момент (корреляция).
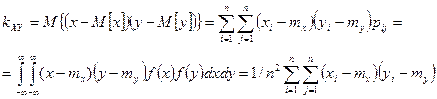
Коэффициент корреляции:
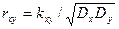
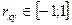
Если x, y – независимы, то rx,y à 0
Если x ~ y, то rx,y à 1
Если x ~ 1/y, то rx,y à -1
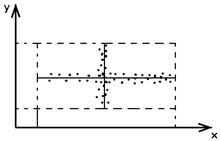 |
Геометрическая интерпритация коэффициента коррелиации.
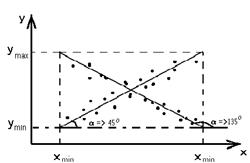 |
Если a стремиться к 0 Ú 90о, то x, y независимы.
Коэффициент автокоррелиации.
Пусть есть последовательность X = {x1, …, xn}, вторую последовательность Y получаем путем сдвига Х на t разрядов kxy.
Основные законы распределения.
1. равномерное распределение
2. нормальное распределение
3. экспонециал (показательное)
4. хи-квадрат
Равномерное распределение.
Непрерывная случайная величина равномерно распределена на [a; b]
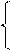 0, x<a
0, x<a
f(x) = c, a £ x £ b (const ³ 0)
0, x>b
Зная, что
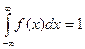
можно определить
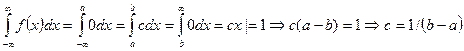
 Нормальное распределение.
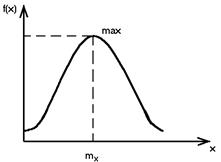
Нормальное распределение.
Это наиболее часто встречающийся закон.
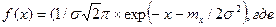
mx – математическое ожидание
s=ÖDx – среднеквадратическое отклонение
M[x] =mx
D[x] = s2
Хорошо описывается погрешность при рассмотрении случайных и псевдослучайных чисел.
Задача1: определить доверительный интервал для матожидания и дисперсии случайных чисел.
t=(x-mx)/sÖ2
В этом случае x=mx+Ö2st
Случайная величина t – называется нормированной случайной величиной с нормальным законом распределения, которая имеет следующую функцию распределения:
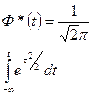
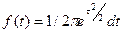 – плотность распределения.
– плотность распределения.
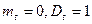
Функция Лапласа.
 1 t
1 t
 Ф*(t)=Ö2p òe-t2/2 dt
Ф*(t)=Ö2p òe-t2/2 dt
-¥
Связь Ф*(t) и Ф(t):
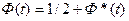
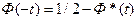
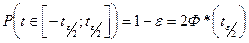
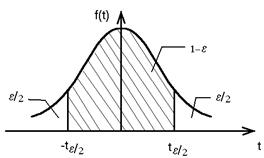
a = 1 - e - доверительная вероятность.
Таблица функции Лапласа для te/2.
mx Î[x-∆; x+∆]
∆ = te/2 ´ s/ÖN
s - среднеквадратическое отклонение.
N – число элементов выборки.
Р = 0,95
Доверительный интервал – это интервал, относительного которого можно с заранее определенной вероятностью близкой к единице утверждать. Что он содержит неизвестное нам значение параметра mx.
Задача2: определить длину последовательности для определения точечных характеристик с заданной вероятностью.
N = (te/2s/∆)2
N – объем выборки, которое с вероятностью р =1 - e обеспечит заданную точность ∆.
Правило трех сигма.
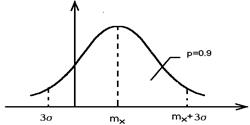 Для случайной величины Х распределенной по нормальному закону ее значение укладывается на участке mx ± 3s
Для случайной величины Х распределенной по нормальному закону ее значение укладывается на участке mx ± 3s
с вероятностью р = 0,9973.
|
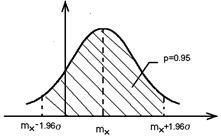
Доверительный интервал для 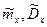 (имперические значения)
(имперические значения)