Применения основной теоремы арифметики
Если у нас есть канонические разложения двух натуральных чисел, то мы можем считать, что эти разложения состоят из одинаковых простых сомножителей, добавляя сомножители вида 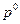 .
.
Например, 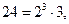
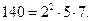 Считают, что
Считают, что 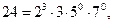
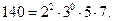
Теорема 2. Пусть 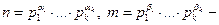 канонические разложения натуральных чисел п и т. Тогда
канонические разложения натуральных чисел п и т. Тогда 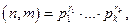 где
где 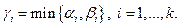
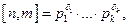 где
где 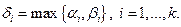
Примеры: 1. 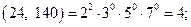
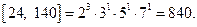
2. Пусть 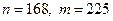 . Найдем их канонические разложения:
. Найдем их канонические разложения:
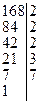
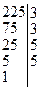
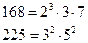
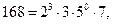
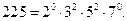
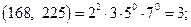
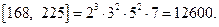
ВОПРОС № 8 Приводимые и неприводимые многочлены. Теорема о разложении многочлена на неприводимые множители над произвольным полем.
Пусть 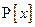 - кольцо многочленов одной переменной с коэффициентами из поля
- кольцо многочленов одной переменной с коэффициентами из поля 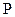 . Как известно, любой многочлен
. Как известно, любой многочлен 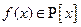 делится на любой элемент
делится на любой элемент 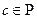 , отличный от
, отличный от
нуля и на многочлены 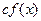
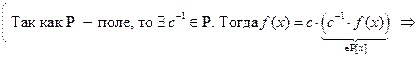
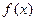
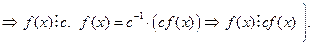 Такие делители называются тривиальными делителями многочлена .
Такие делители называются тривиальными делителями многочлена .
Опр.1. Многочлен 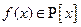 положительной степени из кольца
положительной степени из кольца 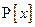 называется неприводимым над полем Р, если
называется неприводимым над полем Р, если 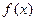 имеет только тривиальные делители в кольце
имеет только тривиальные делители в кольце 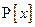 .
.
Опр.2. Многочлен 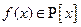 положительной степени называется приводимым над полем Р, если
положительной степени называется приводимым над полем Р, если 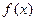 имеет в кольце
имеет в кольце 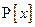 делители, отличные от тривиальных.
делители, отличные от тривиальных.
Если вспомнить определение делимости многочленов, то можем сказать, что многочлен 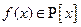 положительной степени называется приводимым над полем Р, если
положительной степени называется приводимым над полем Р, если
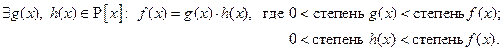 .
.
То есть 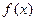 разложен в произведение двух многочленов положительной степени.
разложен в произведение двух многочленов положительной степени.
А многочлен, неприводимый над Р, в виде такого произведения представлен быть не может.
Отметим, что понятие неприводимого многочлена существенно привязано к полю. Один и тот же многочлен может быть неприводим над некоторым полем, а над другим - приводим.
Например, многочлен 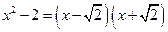 - приводим над
- приводим над  и неприводим над
и неприводим над  .
.
Отметим основные свойства неприводимых многочленов.
1) Любой многочлен первой степени из кольца 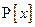 неприводим над Р.
неприводим над Р.
Доказательство: (от противного) Пусть 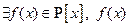 - первой степени - приводимый над полем Р. Тогда
- первой степени - приводимый над полем Р. Тогда 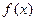 имеет нетривиальные делители, т.е.
имеет нетривиальные делители, т.е. 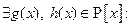

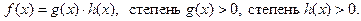 Тогда
Тогда 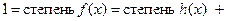
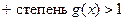 . . Значит
. . Значит 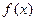 - неприводим над Р. ▲.
- неприводим над Р. ▲.
2) Любой многочлен кольца 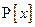 либо взаимно прост с неприводимым над Р многочленом
либо взаимно прост с неприводимым над Р многочленом 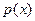 , либо делится на
, либо делится на 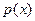 .
.
Доказательство: Пусть 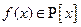 . Обозначим
. Обозначим 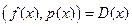 . Тогда
. Тогда
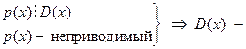 тривиальный делитель многочлена
тривиальный делитель многочлена 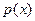 , то есть либо
, то есть либо 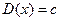 , где
, где 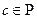 ,
, 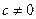 ; либо
; либо 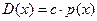 .
.
Если 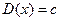 , то
, то 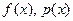 - взаимно просты.
- взаимно просты.
Если 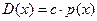 , тогда
, тогда 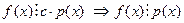 . ▲.
. ▲.
3) Любые два неприводимых над полем Р многочлена 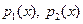 либо взаимно просты, либо ассоциированы.
либо взаимно просты, либо ассоциированы.
Доказательство: Так как 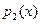 - неприводим, то по свойству 2 либо
- неприводим, то по свойству 2 либо 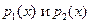 взаимно просты, либо
взаимно просты, либо 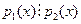 .
.
Если 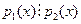 , то т.к.
, то т.к. 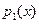 -неприводим, то
-неприводим, то 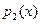 -тривиальный делитель многочлена
-тривиальный делитель многочлена 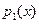 . Но
. Но 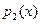 неприводим, поэтому положительной степени
неприводим, поэтому положительной степени 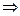
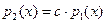 , где
, где 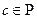 ,
, 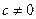
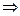
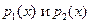 ассоциированы. ▲.
ассоциированы. ▲.
4) Если произведение двух многочленов кольца 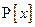 делится не неприводимый над Р многочлен
делится не неприводимый над Р многочлен 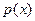 , то хотя бы один из сомножителей делится на
, то хотя бы один из сомножителей делится на 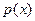 .
.
Доказательство: Пусть 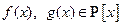 и
и 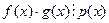 .
.
Если 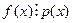 , то всё доказано.
, то всё доказано.
Если 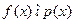 , то по свойству 2,
, то по свойству 2, 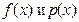 взаимно просты, а тогда по свойствам взаимно простых многочленов
взаимно просты, а тогда по свойствам взаимно простых многочленов 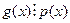 .
.
Следствие свойства 4: Если произведение нескольких многочленов делится на неприводимый многочлен кольца 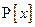 , то хотя бы один из сомножителей делится на этот неприводимый многочлен. (Доказывается методом математической индукции).
, то хотя бы один из сомножителей делится на этот неприводимый многочлен. (Доказывается методом математической индукции).
5) Каждый многочлена кольца 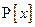 степени
степени 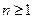 делится хотя бы на один неприводимый над Р многочлен.
делится хотя бы на один неприводимый над Р многочлен.
Доказательство: Индукцией по степени п многочлена 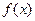 .
.
1) Если 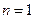 , т.е.
, т.е. 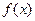 -многочлен первой степени, то он неприводим и
-многочлен первой степени, то он неприводим и 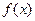 делится на себя.
делится на себя.
2) Допустим, что для всякого многочлена степени, меньшей чем п, теорема верна, т.е. всякий многочлен степени, меньшей чем п, делится на неприводимый многочлен.
3) Докажем утверждение для многочлена 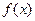 степени п. Если
степени п. Если 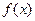 неприводим, то
неприводим, то 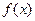 делится на себя и всё доказано.
делится на себя и всё доказано.
Если 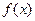 - приводим, то
- приводим, то 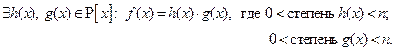
По индуктивному предположению, 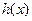 делится на некоторый неприводимый многочлен
делится на некоторый неприводимый многочлен 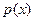 , а тогда имеем:
, а тогда имеем: 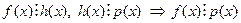 . ▲.
. ▲.
Роль неприводимых над полем Р многочленов усматривается из следующей теоремы:
Теорема. Любой многочлен из кольца 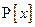 степени
степени 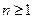 может быть представлен в виде произведения неприводимых над полем Р многочленов и такое представление единственно с точностью до порядка сомножителей и ассоциированности.
может быть представлен в виде произведения неприводимых над полем Р многочленов и такое представление единственно с точностью до порядка сомножителей и ассоциированности.
Доказательство: 1. Существование разложения докажем индукцией по степени п многочлена.
1) Многочлены первой степени неприводимы над Р и разложение для многочлена первой степени тривиально.
2) Допустим, что утверждение справедливо для всех многочленов степени k, меньшей п.
3) Докажем утверждение для многочлена 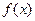 степени п. Если
степени п. Если 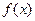 неприводим, то всё доказано.
неприводим, то всё доказано.
Если 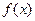 - приводим, то
- приводим, то 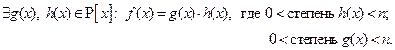
Тогда, по индуктивному предположению, 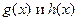 могут быть представлены в виде произведения неприводимых многочленов:
могут быть представлены в виде произведения неприводимых многочленов: 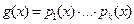 ;
;
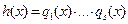 .
.
Следовательно, 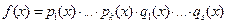 и разложение для
и разложение для 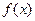 получено.
получено.
2. Единственность разложения докажем индукцией по степени п многочлена.
1) Для многочленов первой степени утверждение справедливо, т.к. они неприводимы над Р.
2) Допустим, что утверждение справедливо для всякого многочлена степени 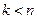 .
.
3) Докажем утверждение для многочлена 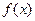 степени п. Допустим, что имеются 2 разложения многочлена
степени п. Допустим, что имеются 2 разложения многочлена 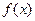 на неприводимые многочлены:
на неприводимые многочлены:
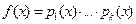 и
и 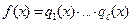
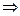
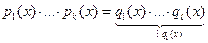
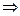
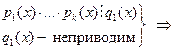 |
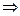 хотя бы один из сомножителей делится на
хотя бы один из сомножителей делится на 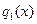 .
.
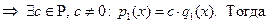 Пусть, например,
Пусть, например, 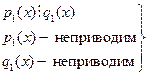
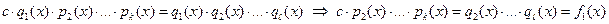 .
.
Степень 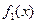 меньше п
меньше п 
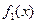 единственным образом, с точностью до порядка сомножителей и ассоциированности, может быть разложен в произведение неприводимых многочленов
единственным образом, с точностью до порядка сомножителей и ассоциированности, может быть разложен в произведение неприводимых многочленов  таким будет и разложение
таким будет и разложение 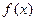 . ▲.
. ▲.
