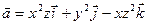Контрольная работа №8. 8.1. Представить двойной интеграл в виде повторного с внешним интегрированием по x и
Вариант 23.
8.1. Представить двойной интеграл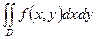 
в виде повторного с внешним интегрированием по x и внешним интегрированием по y, если границы области интегрирования D ограничены кривыми с уравнениями: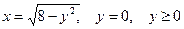 
8.2. Вычислить двойной интеграл по области D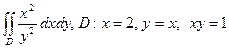 
8.3. Вычислить интеграл, перейдя от прямоугольных декартовых координат
к полярным: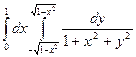 
8.4. Вычислить объем тела, ограниченного заданными поверхностями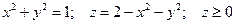 
8.5. Используя формулу Грина, вычислить криволинейный интеграл по замкнутому контуру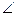 
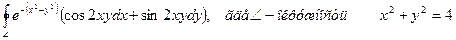
8.6. Вычислить, используя формулу Стокса или непосредственно криволинейный интеграл 2-го рода и пояснить его физический смысл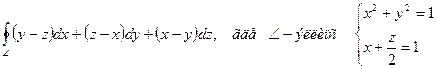 
8.7. Найти массу однородного тела, ограниченного данными поверхностями, считая его плотность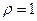 
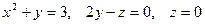
8.8. Выяснить, является ли векторное поле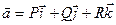 
потенциальным.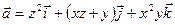 
Контрольная работа №8.
Вариант 24.
8.1. Представить двойной интеграл 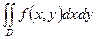в виде повторного с внешним интегрированием по x и внешним интегрированием по y, если границы области интегрирования D ограничены кривыми с уравнениями: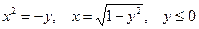 
8.2. Вычислить двойной интеграл по области D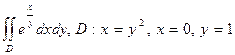 
8.3. Вычислить интеграл, перейдя от прямоугольных декартовых координат
к полярным: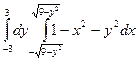 
8.4. Вычислить объем тела, ограниченного заданными поверхностями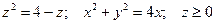 
8.5. Используя формулу Грина, вычислить криволинейный интеграл по замкнутому контуру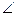 
8.6. Вычислить, используя формулу Стокса или непосредственно криволинейный интеграл 2-го рода и пояснить его физический смысл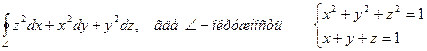 
8.7. Найти массу однородного тела, ограниченного данными поверхностями, считая его плотность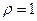 
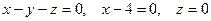
8.8. Выяснить, является ли векторное поле 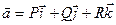потенциальным.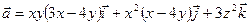 
Контрольная работа №8.
Вариант 25.
8.1. Представить двойной интеграл 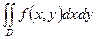в виде повторного с внешним интегрированием по x и внешним интегрированием по y, если границы области интегрирования D ограничены кривыми с уравнениями: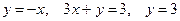 
8.2. Вычислить двойной интеграл по области D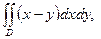 
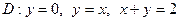
8.3. Вычислить интеграл, перейдя от прямоугольных декартовых координат
к полярным: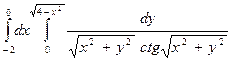 
8.4. Вычислить объем тела, ограниченного заданными поверхностями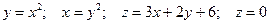 
8.5. Используя формулу Грина, вычислить криволинейный интеграл по замкнутому контуру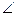 
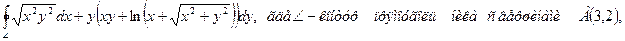
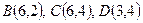
8.6. Вычислить, используя формулу Стокса или непосредственно криволинейный интеграл 2-го рода и пояснить его физический смысл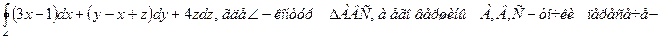 
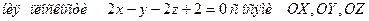
8.7. Найти функцию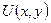 
по заданному ее полному дифференциалу:
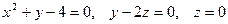
8.8. Выяснить, является ли векторное поле 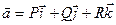потенциальным.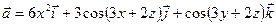 
Контрольная работа №8.
Вариант 26.
8.1. Представить двойной интеграл 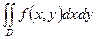в виде повторного с внешним интегрированием по x и внешним интегрированием по y, если границы области интегрирования D ограничены кривыми с уравнениями: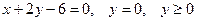 
8.2. Вычислить двойной интеграл по области D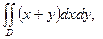 
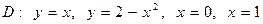
8.3. Вычислить интеграл, перейдя от прямоугольных декартовых координат
к полярным: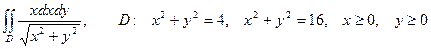 
8.4. Вычислить объем тела, ограниченного заданными поверхностями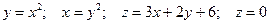
8.5. Используя формулу Грина, вычислить криволинейный интеграл по замкнутому контуру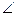 
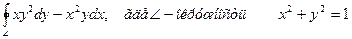
8.6. Вычислить, используя формулу Стокса или непосредственно криволинейный интеграл 2-го рода и пояснить его физический смысл
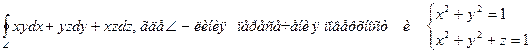
8.7. Найти массу однородного тела, ограниченного данными поверхностями, считая его плотность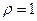 
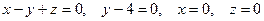
8.8. Выяснить, является ли векторное поле 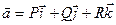гармоническим 