Распределение часов по темам и видам работ

В. Г. ШЕРШНЕВ

МАТЕМАТИЧЕСКИЙ АНАЛИЗ

Часть I. Дифференциальное исчисление

Курс лекций

Москва

ГОУ ВПО «РЭА им. Г. В. Плеханова»

УДК 512

ББК

Ш

Шершнев В. Г.

Ш Математический анализ. Часть I. Дифференциальное исчисление.

Курс лекций для дистанционной формы обучения. – М.: ГОУ ВПО

«РЭА им. Г.В. Плеханова», 2009 г. - 110 с.

Данное пособие составлено на основе лекций, читаемых автором на экономических факультетах РЭА им. Г. В. Плеханова. Содержит теоретический материал по разделам математического анализа: множества, пределы последовательностей и функций, дифференциальное исчисление функций одной и нескольких переменных. Приводится решение характерных заданий. Пособие соответствует программе по математическому анализу для студентов экономических специальностей.

УДК 512

ББК

© ГОУ ВПО «РЭА им. Г. В. Плеханова», 2009

© Шершнев В.Г., 2009

Оглавление

Календарно-тематический план . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Глава I. Введение в математический анализ . . . . . . . . . . . . . . . . . . . . .
1.1. Множества . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.1.1. Определение множества . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.1.2. Операции над множествами . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.1.3. Свойства операций над множествами . . . . . . . . . . . . . . . . . . . . . . .
1.1.4. Декартово произведение множеств . . . . . . . . . . . . . . . . . . . . . . . . .
1.1.5. Модуль числа, его свойства . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.1.6. Грани числовых множеств . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.1.7. Счетные и несчетные множества . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2. Функции, их классификация . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.3. Предел последовательности . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.4. Предел функции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.4.1. Определение предела функции . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.4.2. Геометрический смысл предела . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.4.3. Односторонние пределы. Необходимое и достаточное условия существования предела функции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.5. Бесконечно малые и бесконечно большие функции . . . . . . . . . . . . . .
1.5.1. Определение бесконечно малой функции . . . . . . . . . . . . . . . . . . . .
1.5.2. Свойства бесконечно малых функций . . . . . . . . . . . . . . . . . . . . . . .
1.6. Теоремы о представлении функции в виде суммы предела и бесконечно малой функции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.7. Теоремы о пределах (свойства пределов) . . . . . . . . . . . . . . . . . . . . . . .
1.8. Замечательные пределы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.8.1. Первый замечательный предел . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.8.2. Второй замечательный предел . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.8.3. Применение второго замечательного предела в финансовых вычислениях . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.9. Сравнение бесконечно малых функций . . . . . . . . . . . . . . . . . . . . . . . . .
1.10. Непрерывность функции в точке и на отрезке . . . . . . . . . . . . . . . . . .
1.10.1. Определение непрерывности функции . . . . . . . . . . . . . . . . . . . . .
1.10.2. Действия над непрерывными функциями . . . . . . . . . . . . . . . . . . .
1.10.3. Непрерывность элементарных функций . . . . . . . . . . . . . . . . . . . .
1.10.4. Свойства непрерывных функций . . . . . . . . . . . . . . . . . . . . . . . . . .
1.10.5. Точки разрыва функций . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Глава II. Дифференциальное исчисление функций одной переменной . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.1. Производная функции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.1.1. Определение производной функции . . . . . . . . . . . . . . . . . . . . . . . .
2.1.2. Дифференцируемость функции, ее взаимосвязь с производной и непрерывностью функции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.1.3. Непосредственное нахождение производной . . . . . . . . . . . . . . . . .
2.1.4. Геометрический смысл производной. . . . . . . . . . . . . . . . . . . . . . . .
2.1.5. Механический смысл производной . . . . . . . . . . . . . . . . . . . . . . . . .
2.1.6. Правила дифференцирования функций . . . . . . . . . . . . . . . . . . . . . .
2.1.7. Вывод производных основных элементарных функций . . . . . . . .
2.1.8. Сводка формул. Правила дифференцирования и таблица производных . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.1.9. Производные высших порядков . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.1.10. Эластичность функции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.1.11. Геометрический смысл эластичности . . . . . . . . . . . . . . . . . . . . . .
2.1.12. Экономический смысл эластичности . . . . . . . . . . . . . . . . . . . . . . .
2.1.13. Свойства эластичности функции . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2. Дифференциал функции одной переменной . . . . . . . . . . . . . . . . . . . . .
2.2.1. Определение дифференциала функции . . . . . . . . . . . . . . . . . . . . . .
2.2.2. Геометрический смысл дифференциала . . . . . . . . . . . . . . . . . . . . . .
2.2.3. Свойства дифференциала . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2.4. Применение дифференциала для приближенных вычислений . . .
2.2.5. Дифференциалы высших порядков . . . . . . . . . . . . . . . . . . . . . . . . .
2.3. Теоремы о дифференцируемых функциях . . . . . . . . . . . . . . . . . . . . . .
2.3.1. Теорема Ролля . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.3.2. Геометрический смысл теоремы Ролля . . . . . . . . . . . . . . . . . . . . . .
2.3.3. Примеры использования теоремы Ролля . . . . . . . . . . . . . . . . . . . . .
2.3.4. Теорема Лагранжа о конечном приращении функции . . . . . . . . . .
2.3.5. Геометрический смысл теоремы Лагранжа . . . . . . . . . . . . . . . . . . .
2.3.6. Теорема Коши . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.3.7. Раскрытие неопределенностей при нахождении пределов. Правило Лопиталя . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.3.8. Применение правила Лопиталя для раскрытия неопределенностей типа степени . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.4. Формулы Тейлора и Маклорена . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.4.1. Формула Тейлора. Остаточный член в форме Лагранжа . . . . . . .
2.4.2. Формула Маклорена . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.4.3. Разложение основных элементарных функций по формуле Маклорена . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.4.4. Применение формулы Маклорена для вычисления пределов и значений функций . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.5. Исследование функций . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.5. 1.Необходимый и достаточный признаки монотонности функций .
2.5.2. Определение экстремума функции . . . . . . . . . . . . . . . . . . . . . . . . . .
2.5.3. Необходимый признак экстремума функции . . . . . . . . . . . . . . . . .
2.5.4. Первый достаточный признак экстремума функции (с использованием первой производной) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.5.5. Второй достаточный признак экстремума функции (с использованием производной второго порядка) . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.5.6. Определение выпуклости, вогнутости графика функции, точки перегиба . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.6.7. Достаточный признак выпуклости, вогнутости графика функции
2.5.8. Необходимый признак существования точки перегиба . . . . . . . .
2.5.9. Достаточный признак существования точки перегиба . . . . . . . . . .
2.5.10. Асимптоты графика функции . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.5.11. Построение графика функции . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Глава III. Дифференциальное исчисление функций нескольких переменных . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.1. Определение функции нескольких переменных . . . . . . . . . . . . . . . . . .
3.2. Предел функции нескольких переменных . . . . . . . . . . . . . . . . . . . . . . .
3.3. Бесконечно малые функции нескольких переменных . . . . . . . . . . . . .
3.4. Свойства пределов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.5. Непрерывность функций нескольких переменных. Точки и линии разрыва . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.6. Частные приращения и частные производные функции нескольких переменных . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.6.1. Геометрический смысл частных производных . . . . . . . . . . . . . . . .
3.7. Дифференцируемость функции нескольких переменных . . . . . . . . . .
3.8. Необходимые условия дифференцируемости функции нескольких переменных . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.9. Достаточные условия дифференцируемости функции нескольких переменных . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.10. Полный дифференциал функции нескольких переменных . . . . . . .
3.10. 1. Применение полного дифференциала функции нескольких переменных для приближенных вычислений . . . . . . . . . . . . . . . . . . . . . . . . . .
3.11. Частные производные высших порядков . . . . . . . . . . . . . . . . . . . . . . .
3.12. Дифференциалы высших порядков . . . . . . . . . . . . . . . . . . . . . . . . . .
3.13. Частные производные сложной функции нескольких переменных
3.14. Производная функции, заданной неявно. . . . . . . . . . . . . . . . . . . . . .
3.15. Производная функции по направлению. . . . . . . . . . . . . . . . . . . . . . .
3.16. Градиент функции, его свойства . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.17. Формула Тейлора для функций двух переменных . . . . . . . . . . . . . .
3.18. Локальный экстремум функции нескольких переменных . . . . . . . .
3.19. Необходимый признак локального экстремума . . . . . . . . . . . . . . . .
3.20. Достаточный признак локального экстремума функции двух переменных . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.21. Метод наименьших квадратов (МНК) . . . . . . . . . . . . . . . . . . . . . . . .
3.22. Условный экстремум функции нескольких переменных . . . . . . . . .
3.22.1. Постановка задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.22.2. Нахождение критических точек . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.22.3. Метод множителей Лагранжа . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.22.4. Достаточный признак условного экстремума функции нескольких переменных . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.23. Абсолютный экстремум функций нескольких переменных . . . . . .
Вопросы к экзамену . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Литература . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

КАЛЕНДАРНО-ТЕМАТИЧЕСКИЙ ПЛАН

Распределение часов по темам и видам работ

Наименование разделов и тем	Всего	Аудиторные часы	Самостоят. работа	Форма контр.
Лекци	Семин.
Раздел 1.Введение в математический анализ
Тема 1.Множества и функции
Тема 2.Предел числовой последовательности
Тема 3.Предел функции					Контр. работа
Тема 4.Сравнение бесконечно малых функций. Непрерывность функции
Раздел 2.Дифференциальное исчисление функций одной переменной
Тема 5.Производная функции
Тема 6.Дифференциал функции. Предельный анализ
Тема 7.Теоремы о дифференцируемых функциях. Правило Лопиталя.					Контр. работа
Тема 8.Применение дифференциального исчисления для исследования функций					Контр. работа
Раздел 3. Дифференциальное исчисление функций нескольких переменных
Тема 9.Функции нескольких переменных: определение, предел, непрерывность, частные производные
Тема 10.Дифференцируемость функций нескольких переменных
Тема 11.Экстремум функции нескольких переменных
Тема 12.Метод наименьших квадратов					Контр. работа
Всего					Экзам.

Глава I. Введение в математический анализ

Множества

Определение множества

Математическим анализом называется раздел математики, занимающийся исследованием функций на основе идеи бесконечно малой функции.

Основными понятиями математического анализа являются величина, множество, функция, бесконечно малая функция, предел, производная, интеграл и т. д.

Величиной называется все, что может быть измерено и выражено числом.

Множеством называется совокупность некоторых элементов. Элементами множества могут быть числа, фигуры, предметы, понятия и т. п.

Множества обозначаются прописными буквами, а элементы множеств - строчными буквами. Элементы множеств заключаются в фигурные скобки. Если элемент х принадлежит множеству Х, то записывают х Î Х (Î - принадлежит). Если множество А является частью множества В, то записывают А Ì В (Ì - содержится).

Множество может быть задано одним из двух способов: перечислением и с помощью определяющего свойства.

Например, перечислением заданы следующие множества:

1) 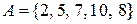- множество чисел;

2) 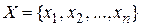- множество некоторых элементов ;

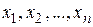2) 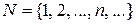- множество натуральных чисел;

3) 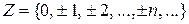- множество целых чисел.

В общем случае множество элементов х с помощью определяющего свойства 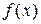записывается в виде .

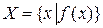Например:

1) 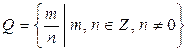- множество рациональных чисел;

2) 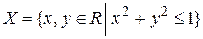- множество вещественных чисел x, y, для которых сумма квадратов не превосходит единицу.

Если множество не содержит ни одного элемента, то оно называется пустым множеством и записывается .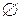

При записи математических выражений часто используются кванторы.

Квантором называется логический символ, который характеризует следующие за ним элементы в количественном отношении.

" - квантор общности, используется вместо слов «для всех», «для любого».

$ - квантор существования, используется вместо слов «существует», «имеется». Используется также сочетание символов $!, которое читается как существует единственный.

Например, запись " xÎD $! y Î E означает, что для любого x, принадлежащего множеству D, существует единственное y, принадлежащее множеству E.

Операции над множествами

Два множества А и В равны (А = В), если они состоят из одних и тех же элементов.

Например, если A = {1, 2, 3, 4}, B = {3, 1, 4, 2}, то А = В.

Объединением (суммой) множеств А и В называется множество А È В, элементы которого принадлежат хотя бы одному из этих множеств.

Например, если A = {1, 2, 4}, B = {3, 4, 5, 6}, то А È В = {1, 2, 3, 4, 5, 6}.

Если объединяются n множеств, то записывают .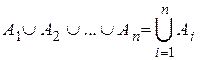

Пересечением (произведением) множеств А и В называется множество А Ç В, элементы которого принадлежат как множеству А, так и множеству В.

Например, если A = {1, 2, 4}, B = {3, 4, 5, 2}, то А Ç В = {2, 4}.

Если множество является пересечением n множеств, то записывают .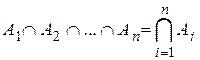

Разностью множеств А и В называется множество А \ В, элементы которого принадлежат множеству А, но не принадлежат множеству В.

Например, если A = {1, 2, 3, 4}, B = {3, 4, 5}, то А \ В = {1, 2}.

Симметрической разностью множеств А и В называется множество А Δ В, являющеесяобъединением разностей множеств А \ В и В \А , т. е.

А Δ В = (А \ В)È (В \А).

Например, если A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, то А Δ В = {1, 2}È{5, 6}= = {1, 2, 5, 6}.