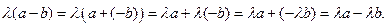П. 5. Определение группы

Опр.6. Пусть 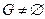, * - бинарная операция на множестве 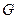. называется группой, если выполняются следующие условия (аксиомы группы):

1) 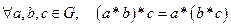, т.е. операция * ассоциативна;

2) 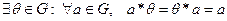, т.е. в множестве 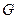существует нейтральный относительно операции * элемент;

3) 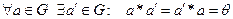, т.е. для каждого элемента а множества 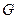существует в множестве 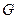симметричный к нему элемент .

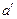Опр.7. Группа 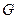называется коммутативной (абелевой), если операция * коммутативна.

Опр.8. Группа 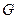называется конечной, если 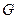- конечное множество; при этом число элементов множества 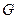называют порядком группы .

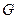Если 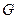- бесконечное множество, то группа 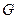называется бесконечной группой.

Свойства группы

1) Нейтральный элемент в группе единственный (теорема 1).

2) Каждый элемент группы имеет единственный симметричный к нему элемент (теорема 2).

3) 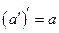. Симметричный к симметричному для элемента а элемент есть сам элемент а.

Доказательство: По определению симметричного элемента имеем, что 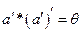. Тогда . ▲

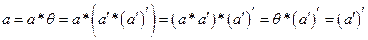4) В группе выполняются законы сокращения, т.е. 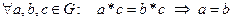и .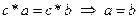

Доказательство: Пусть 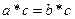. Тогда

.

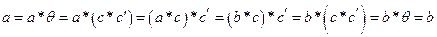Аналогично доказывается другой закон сокращения. ▲

5) В группе 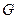каждое из уравнени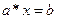й и 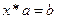имеет единственное решение для любых .

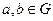Доказательство: Действительно, т.к. 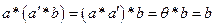, то элемент 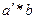является решением уравнения .

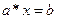Если с -ещё одно решение этого уравнения, т.е. 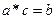, то имеем

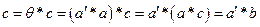, т.е. . ▲

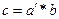6) 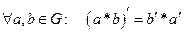(Теорема 2).

Аддитивная и мультипликативная запись группы

Аддитивная запись

Пусть 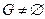, «+» - бинарная операция на 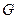. 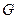-группа, если:

1) ;

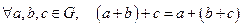2) ;

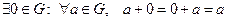3) .

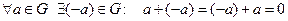Группу 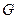при этом называют группой по сложению или аддитивной группой.

Мультипликативная запись

Пусть 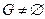, «∙» - бинарная операция на 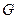. 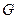-группа, если:

1) ;

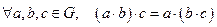2) ;

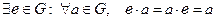3) .

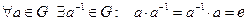Группу 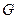при этом называют группой по умножению или мультипликативной группой.

Примеры групп:

1. Аддитивные группы целых, рациональных, действительных, комплексных чисел. При этом они абелевы (всякое кольцо есть группа по сложению).

2. Множество целых четных чисел аддитивная абелева группа.

3. Множество отличных от нуля элементов любого поля образует абелеву группу по умножению. Эта группа называется мультипликативной группой поля.

Таким образом, мы имеем мультипликативные группы полей рациональных, действительных и комплексных чисел.

4. Группу по умножению составляют все положительные действительные числа. Эта группа коммутативна.

5. Пусть - множество всех корней n-степени из 1 в поле комплексных чисел. Известно, что 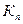- конечное множество, содержащее n элементов, т.е. все корни находятся по формуле 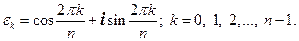Легко проверить, что 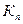- группа по умножению, притом абелева и конечная порядка n.

Этот пример показывает, что для любого натурального числа n существует конечная мультипликативная группа порядка n.

6. Пусть m - натуральное число. 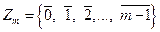- множество классов вычетов по модулю m. Это множество по сложению образует абелеву конечную группу порядка m. Нейтральным элементом группы 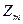является класс 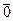, противоположным элементом для класса 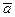является класс .

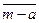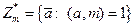- мультипликативная группа.

7. Множество всех движений плоскости (пространства) относительно их композиции образует группу, притом коммутативную. Действительно, из геометрии известно, что композиция 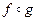движений f и g есть снова движение; преобразование 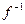, обратное движению f, есть также движение; тождественное преобразование, очевидно, является движением, ассоциативный закон 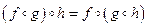выполняется для любых преобразований.

8. Аналогично устанавливается, что множество всех подобий плоскости (пространства), множество всех аффинных преобразований плоскости (пространства) являются группами относительно композиции преобразований.

9. Множество всех квадратных матриц n-ого порядка над полем P является аддитивной абелевой группой.

10. Множество всех обратимых квадратных матриц n-oго порядка на полем P - мультипликативная группа; при 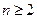некоммутативна.

11. Пусть 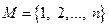- конечное n-элементное множество. Взаимно однозначное отображение 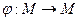называется подстановкой n-ной степени.

Подстановку 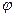обычно записывают в следующем виде: 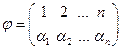, указывая во второй строке образы чисел 1, 2,…, п, т.е. 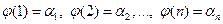. Известно, что существует п! подстановок п-ной степени. Умножение 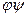двух подстановок - это результат выполнения сначала подстановки 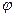, а затем подстановки 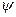. Множество 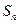всех подстановок п-ной степени есть группа по умножению, при этом конечная, порядка п!. Эта группа при 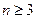является некоммутативной. Она называется симметрической группой п-ной степени.

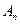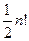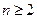12. Множество всех четных подстановок п-ной степени также образует группу по умножению. Эта группа конечна и имеет порядок при . При 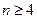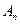- некоммутативная группа, а группа 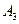коммутативна. Группа 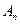называется знакопеременной группой п-ной степени.

ВОПРОС № 2 Определение кольца. Свойства. Коммутативные кольца. Делители нуля. Примеры колец.

Опр.1. Непустое множество К, в котором определены две бинарные операции – сложение «+» и умножение «×», называется кольцом, если выполняются следующие условия (аксиомы кольца):

1) 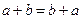для всех а и b из К;

2) 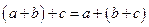для всех ;

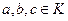3) существует элемент 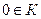такой, что 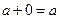для любого 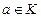(элемент 0 – нулевой элемент кольца);

4) для каждого элемента 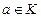существует элемент 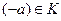такой, что 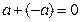(элемент (- а) при этом называют противоположным для элемента а);

5) 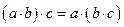для всех ;

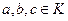6) 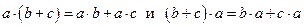для всех .

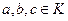Часто в математике рассматривают кольца, удовлетворяющие дополнительным требованиям.

Опр.2. Кольцо К называется коммутативным, если умножение удовлетворяет условию коммутативности, т.е. 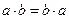для всех .

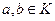Опр.3. Если в кольце К имеется такой элемент 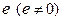, что 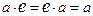для всех 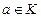, то говорят, что К -кольцо с единицей, а элемент 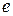называют единицей кольца.

Аксиомы 1) – 4) показывают, что любое кольцо является абелевой (коммутативной) группой по сложению, которую называют аддитивной группой кольца.

Из свойств групп следует, что во всяком кольце выполняются следующие свойства:

I.В кольце К существует единственный нулевой элемент.

II.Каждый элемент а кольца К имеет единственный противоположный элемент .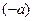

III.В кольце имеет место закон сокращения, т.е. , .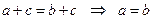

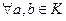IV. .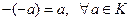

V. .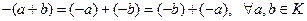

VI.Уравнение 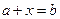для любых элементов 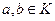имеет единственное решение .

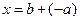Сумма 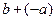обозначается 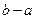и называется разностью элементов 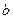и а. Таким образом, в кольце появляется еще одна бинарная операция – вычитание, при этом .

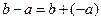Отметим некоторые свойства разности:

1) 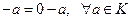. Действительно, .

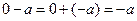2) 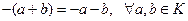. Действительно, .

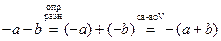3) 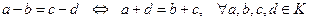. Действительно, .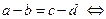

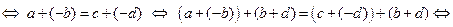
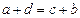4) 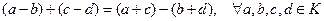. Действительно,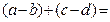

.

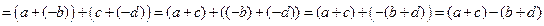5) 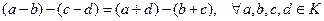. Действительно,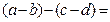

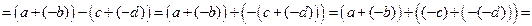
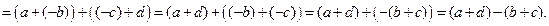
Дальнейшие свойства кольца:

VII.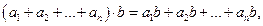

.

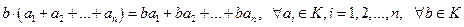VIII.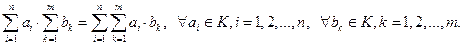

Свойства VII и VIII легко доказываются методом математической индукции.

IX. 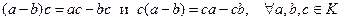, т.е. дистрибутивные законы выполняются и для разности элементов кольца.

Действительно,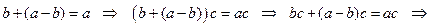

.

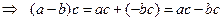X. .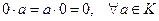

Действительно,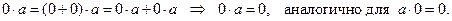

XI. .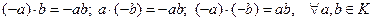

Действительно,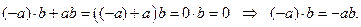

Аналогично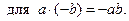

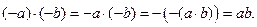(«минус» на «минус» дает «плюс»)

XII. .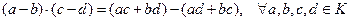

Действительно,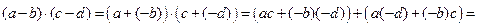

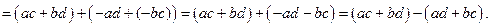
Опр.4. Элементы 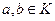называются делителями нуля, если 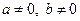, но .

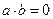Примеры колец:

1. Каждое из следующих множеств – 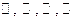является кольцом. Все они являются коммутативными кольцами с единицей и не содержат делителей нуля.

2. Множество всех четных целых чисел является коммутативным кольцом без единицы и делителей нуля.

3. Множество 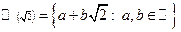является коммутативным кольцом с единицей и без делителей нуля.

4. Множество 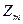классов вычетов по модулю m является коммутативным кольцом с единицей 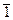. При составном модуле m кольцо 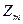содержит делители нуля. Например, в кольце 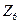классы вычетов 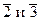являются делителями нуля, т.к. 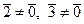, но .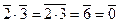

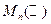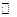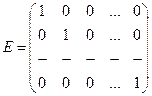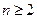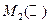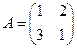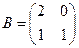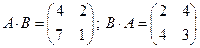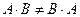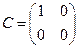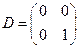5. Множество квадратных матриц n-ого порядка над полем действительных чисел является кольцом с единицей. Единицей является матрица . Это кольцо некоммутативное при и содержит делители нуля. Например, в кольце если , , то и мы видим, что . Матрицы и отличны от нуля – нулевой матрицы 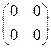, но .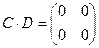

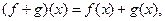
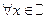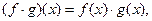
6. Множество функций, определенных для всех действительных значений х и принимающих действительные значения, является коммутативным кольцом с единицей. Сложение и умножение функций определяется при этом «поточечно»: , 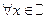. Нулевой элемент - функция 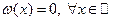, единичный элемент - функция 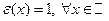. В этом кольце имеются делители нуля, например, следующие функции: .

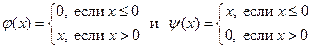7. Множество многочленов от переменной х с коэффициентами из поля Р образует кольцо 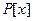. Это кольцо коммутативное, содержит единицу и не имеет делителей нуля.

ВОПРОС № 3 Определение поля. Свойства. Характеристика поля. Примеры полей.

Опр.1. Полем называется множество Р, в котором определены 2 бинарные операции – сложение «+» и умножение «×», удовлетворяющие следующим условиям (аксиомы поля):

1⁰ Сложение ассоциативно, т.е.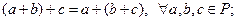

2⁰ Сложение коммутативно, т.е.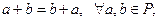

3⁰ 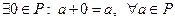(0 - нулевой элемент);

4⁰ 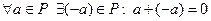(-а - противоположный к элементу а элемент);

5⁰ Умножение ассоциативно, т.е.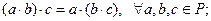

6⁰ Умножение коммутативно, т.е.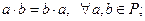

7⁰ 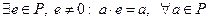(е - нейтральный элемент);

8⁰ 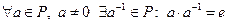( 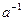- обратный к элементу а элемент);

9⁰ Имеет место дистрибутивный закон умножения относительно сложения (т.е. умножение и сложение связаны дистрибутивным законом): .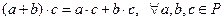

Видим, что поле является кольцом (1⁰, 2⁰, 3⁰, 4⁰, 5⁰, 9⁰), причем коммутативным (6⁰) и с единицей (7⁰).

Поэтому можно дать другое определение поля:

Полем называется коммутативное кольцо с единицей, в котором 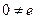и любой ненулевой элемент обратим (т.е. имеет обратный элемент).

Поэтому в поле справедливы все свойства кольца, а именно:

1) В поле P существует единственный нулевой элемент.

2) Каждый элемент поля P имеет единственный противоположный элемент.

3) В поле P имеет место закон сокращения: .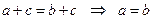

4) Уравнение 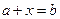имеет единственное решение 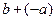, которое называется разностью элементов b и a обозначается 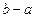, т.е. в поле P можно рассматривать бинарную операцию – вычитание и установить все свойства вычитания.

5) Единичный элемент поля P единственный.

6) .

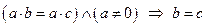Доказательство: Пусть 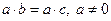, тогда, т.к. 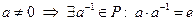. Значит, ▲.

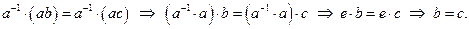7) Каждый отличный от нуля элемент а имеет единственный обратный к нему элемент.

8) .

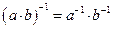9) В поле нет делителей нуля, т.е. нет ненулевых элементов, произведение которых было бы равно нулю.

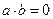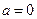Доказательство: Покажем, что если , то или 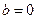. Действительно, пусть 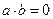. Если 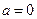, то все доказано. Пусть 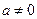, тогда ▲.

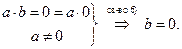10) Для любых элементов а и b, 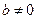поля Р, уравнение 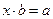имеет единственное решение 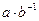. Это решение данного уравнения называется частным элементов а и b и обозначается .

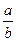Итак, частное любых двух элементов а и b, 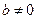поля Р однозначно определено и .

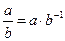Свойства частного:

1. 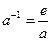. Действительно,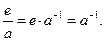

2. 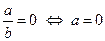. Действительно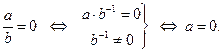

3. .

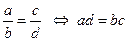Доказательство: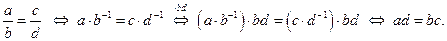

4. .

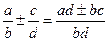Доказательство: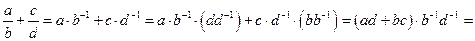

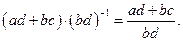Разность аналогично.

5. .

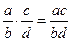Доказательство: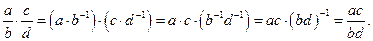

6.

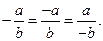
Доказательство: 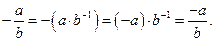Но из свойства 3) следует, что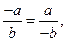

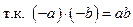значит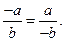

7.

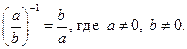
Действительно,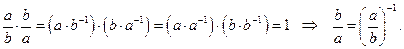

Примеры полей:

1. Каждое из следующих множеств - 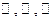является полем.

2. 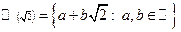- поле.

3. Множество всех дробно-рациональных функций с действительными коэффициентами есть поле, т.е. множество 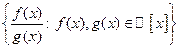- поле.

4. 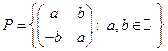- поле; 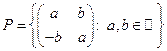- поле.

Все перечисленные поля являются бесконечными, т.е. содержат бесконечно много элементов. Существуют, однако, поля, состоящие из конечного числа элементов.

5. Рассмотрим кольцо 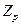классов вычетов по простому модулю р, то есть 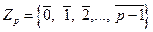и покажем, что это поле.

Доказательство: если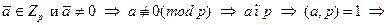

.

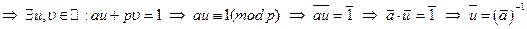6. Отметим, что если модуль m не является простым числом, то кольцо 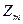классов вычетов по данному модулю полем не является. Действительно, т.к. m -составное число, то 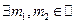такие, что 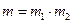, причем 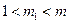и 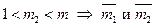– делители нуля, т.к. 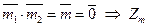не является полем.

Характеристика поля

Не все свойства числовых полей сохраняются в случае произвольных полей. Так, складывая число 1 само с собою несколько раз, т.е. беря любое целое положительное кратное единицы, мы никогда не получим нуля 0. Это имеет место не для всех полей. Например, рассмотрим поле 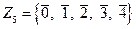, в нем 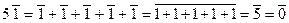, то есть в поле 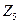нашлось целое кратное единицы 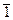, равное нулю .

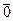Опр.2. Пусть е – единица поля Р. Наименьшее натуральное число m такое, что 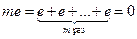(если оно существует), называется характеристикой поля Р.

Если же любое натуральное кратное единицы е поля Р отлично от нуля, то говорят, что поле Р имеет характеристику нуль.

Очевидно, что характеристика поля 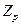, где р -простое число, равна р.

Справедлива следующая теорема.

Теорема. Характеристикой поля является либо нуль, либо простое число.

Доказательство: Если характеристика поля Р есть нуль, то все доказано.

Пусть она не есть нуль, а натуральное число m и допустим, что m не является простым числом. Число 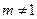, т.к. в противном случае 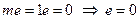, чего в поле нет. Так как m -составное число 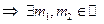такие, что 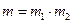, причем 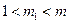и 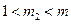. Тогда 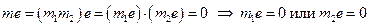(т.к. в поле нет делителей нуля), а это означает, что m не является наименьшим натуральным числом с таким свойством, что противоречит тому, что m -характеристика поля P, значит m -простое число. ▲

ВОПРОС № 4 Определение векторного пространства. Свойства. Примеры векторных пространств.

Опр.1. Пусть - аддитивная абелева группа, т.е. на определена бинарная операция «+» такая, что: 1) «+» - ассоциативна;

2) «+» - коммутативна;

3) ;

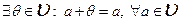4) .

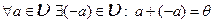Р - поле. Пусть также определено действие умножения элементов на элементы поля Р, т.е. указан закон, по которому 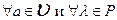ставится в соответствие единственный элемент 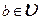, который называется произведением λ на а и обозначается 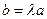. Тогда называется векторным пространством над полем Р, если:

1. .

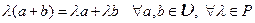2. .

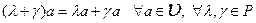3. .

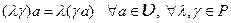4. .

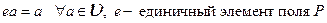Элементы называются векторами, а элементы поля Р – скалярами.

Замечание: - группа по сложению, нейтральный элемент относительно «+» обозначаем 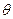. Нулевой элемент поля Р обозначаем 0.

Свойства:

Так как - группа относительно «+», то для выполнены все свойства группы, а именно: 1) нулевой вектор 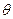единственный;

2) Для любого вектора 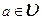существует единственный противоположный вектор ;

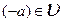3) Уравнение 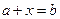имеет единственное решение . Это решение 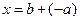обозначается 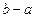и называется разностью векторов .

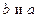Отметим дальнейшие простейшие свойства векторного пространства:

4) 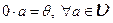(0 – нулевой элемент поля Р, 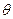- нулевой вектор из ).

Доказательство: 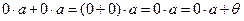. Итак,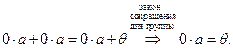

5) .

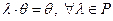Доказательство: .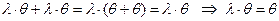

6) Если 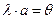, то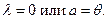

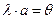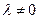Доказательство: пусть и , покажем, что тогда 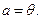Так как 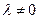, то 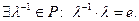Теперь имеем, что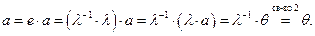

7) .

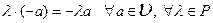Доказательство: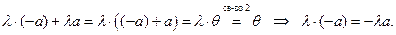

8) .

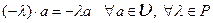Доказательство: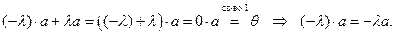

9) .

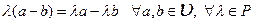Доказательство: