Средняя производительность
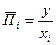 – средний темп изменения у при увеличении фактора от нуля до заданного значения хi .
– средний темп изменения у при увеличении фактора от нуля до заданного значения хi .
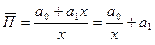 .
.
при 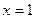
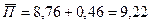 ;
;
при 
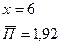 ;
;
при 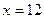
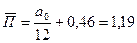 .
. 
Коэффициент эластичности
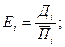
Для линейной регрессии коэффициент эластичности равен:
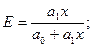
Коэффициент эластичности показывает на сколько процентов изменится результат производства( у) при изменении фактора (х) на 1%.
При 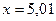 , коэффициент эластичности равен:
, коэффициент эластичности равен:
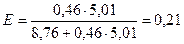 , т.е. при изменении фактора на 1% результат изменится на 0,21%.
, т.е. при изменении фактора на 1% результат изменится на 0,21%.
при х=52
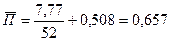 .
.
Коэффициент эластичности:
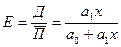 ;
;
при х=50 коэффициент эластичности равен
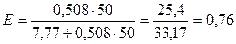 ,
,
т.е. при изменении (х) на 1% величина (у) изменится на 0,76%.
 Демонстрационная задача № 3
Демонстрационная задача № 3
Используя данные о фактической величине потерь на холостые повороты и заезды тракторных агрегатов при выполнении полевых работ в зависимости от длины гона, определить расчетные значения величины потерь, величину корреляционного отношения, его ошибку, критерий достоверности и доверительные границы корреляционного отношения.
Таблица 7
Исходные данные
| № п/п (j) | Фактическая величина потерь, % (yj) | Длина гона, км (xj) |
| 16.8 | 0.4 | |
| 10.8 | 0.7 | |
| 6.2 | 1.0 | |
| 6.0 | 1.3 | |
| 4.0 | 1.6 | |
| 3.8 | 1.9 | |
| 3.1 | 2.2 | |
| 16.0 | 0.5 | |
| 13.8 | 0.6 | |
| 12.1 | 0.7 | |
| 10.0 | 0.8 | |
| 9.0 | 0.9 | |
| 5.8 | 1.0 | |
| 8.1 | 1.1 |
Решение
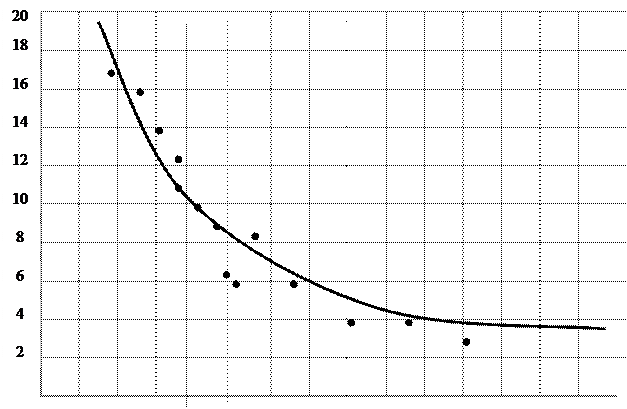
Для определения зависимости между значением фактической величины потерь на холостые повороты и заезды тракторных агрегатов при выполнении полевых работ и длиной гона построим график в двухмерной системе координат (x,y), где у – величины потерь на холостые повороты (%) и заезды, х – длина гона (км) (рис. 3).
Рисунок свидетельствует о наличии гиперболической зависимости. Уравнение гиперболы имеет вид y=a0+a1/x.
Для расчета параметров «a0» и «a1» решается система уравнений:
 |
0 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 2,0 2,2 2,4 2,6 2,8
Рис. 3. Графическое представление зависимости между значением фактической величины потерь на холостые повороты и заезды тракторных агрегатов и длиной гона. Точками показаны результаты наблюдений
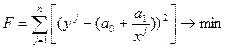
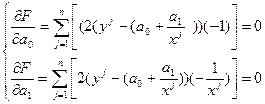 ;
;
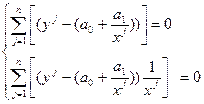 ;
;
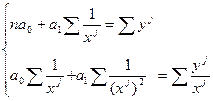 .
.
Промежуточные вычисления, необходимые для решения системы нормальных уравнений, приведены в табл. 8.
Таблица 8
Расчет коэффициентов системы нормальных уравнений
(случай гиперболической регрессии)
| № п/п (j) | Фактическая величина потерь , % (yj) | Длина гона, км (xj) | 1/хj | 1/(хj)2 | yj/xj | Расчетная величина потерь, %, ŷj |
| 16.8 | 0.4 | 2.5 | 6.25 | 42.0 | 19.32 | |
| 10.8 | 0.7 | 1.429 | 2.04 | 15.429 | 11.35 | |
| 6.2 | 1.0 | 1.0 | 1.0 | 6.2 | 8.17 | |
| 6.0 | 1.3 | 0.769 | 0.59 | 4.615 | 6.45 | |
| 4.0 | 1.6 | 0.625 | 0.39 | 2.5 | 5.38 | |
| 3.8 | 1.9 | 0.526 | 0.28 | 2.0 | 4.64 | |
| 3.1 | 2.2 | 0.455 | 0.21 | 1.409 | 4.11 | |
| 16.0 | 0.5 | 2.0 | 4.0 | 32.0 | 15.60 | |
| 13.8 | 0.6 | 1.666 | 2.78 | 23.0 | 13.12 | |
| 12.1 | 0.7 | 1.429 | 2.04 | 18.714 | 11.35 | |
| 10.0 | 0.8 | 1.25 | 1.56 | 16.25 | 10.02 | |
| 9.0 | 0.9 | 1.111 | 1.23 | 11.444 | 8.99 | |
| 5.8 | 1.0 | 1.0 | 1.0 | 9.2 | 8.17 | |
| 8.1 | 1.1 | 0.909 | 0.83 | 7.364 | 7.49 | |
| S | 125,5 | 16.669 | 24.20 | 192.125 |
Используя результаты расчёта табл. 8 запишем систему нормальных уравнений в виде:
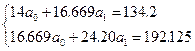 ;
; 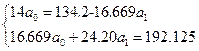 ;
;
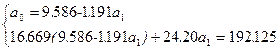 ;
; 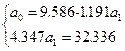 ;
;
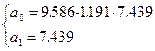 ;
; 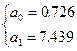 .
.
Сглаженная зависимость потерь на холостые повороты и заезды тракторных агрегатов от длины гона имеет вид:
y=0.726+7.439/x.
Поскольку зависимость между длиной гона и величиной потерь на холостые повороты и заезды тракторных агрегатов носит нелинейный характер, тесноту нелинейных связей можно характеризовать выборочным корреляционным отношением:
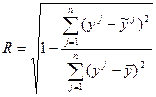
О степени линейной корреляции можно судить по значению ryx .
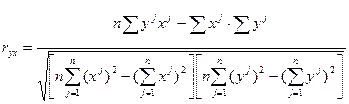 .
.
Для расчета величин (y-ŷ)2, ( 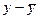 )2 составим таблицу 9.
)2 составим таблицу 9.
Таблица 9
Таблица для расчета корреляционного отношения
| № п/п (j) | Фактическая величина потерь , % (yj) | 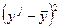 | Расчетная величина потерь, %, yj | 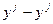 | 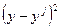 |
| 16.8 | 51,84 | 19.32 | -2,52 | 6,35 | |
| 10.8 | 1,44 | 11.35 | -0,55 | 0,30 | |
| 6.2 | 11,56 | 8.17 | -1,97 | 3,88 | |
| 6.0 | 12,96 | 6.45 | -0,45 | 0,20 | |
| 4.0 | 31,36 | 5.38 | -1,38 | 1,90 | |
| 3.8 | 33,64 | 4.64 | -0,84 | 0,71 | |
| 3.1 | 42,25 | 4.11 | -1,01 | 1,02 | |
| 16.0 | 40,96 | 15.60 | 0,40 | 0,16 | |
| 13.8 | 17,64 | 13.12 | 0,68 | 0,46 | |
| 12.1 | 12,25 | 11.35 | 1,75 | 3,06 | |
| 10.0 | 11,56 | 10.02 | 2,98 | 8,88 | |
| 9.0 | 0,49 | 8.99 | 1,31 | 1,72 | |
| 5.8 | 0,16 | 8.17 | 1,03 | 1,06 | |
| 8.1 | 2,25 | 7.49 | 0,61 | 0,37 | |
| S | 134.2 | 270,36 | 134,16 | 30,07 | |
| ∑/п | 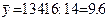 |
Подставляя найденные значения величин в формулу, получим:
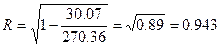 .
.
Стандартная (среднеквадратическая) ошибка определения коэффициента корреляции и корреляционного отношения может быть оценена по формулам:
при 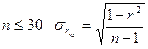 ;
; 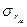 =______
=______ 
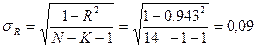 .
.
где N – объем выборки (случай, когда N<30);
K – число факторов.
Достоверность расчёта корреляционного отношения высока.
Очень большое значение выборочного корреляционного отношения и малая погрешность его определения говорят об адекватности принятой регрессионной зависимости реальной статистической картине, о верности выбранной гиперболической зависимости между величинами у и х.
Степень влияния фактора на результат, определяется значением коэффициента детерминации.
Коэффициент детерминации вычисляется по формуле:
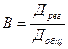 ; где Дрег и Дост – дисперсии отклонений сглаженных значений ŷj от среднего наблюдаемого
; где Дрег и Дост – дисперсии отклонений сглаженных значений ŷj от среднего наблюдаемого 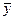 и отклонений наблюдаемых величин
и отклонений наблюдаемых величин 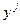 от сглаженного
от сглаженного 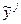 .
.
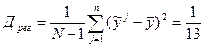
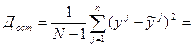
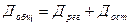
Таблица 10
Таблица для расчёта коэффициента детерминации
| N n/n | 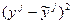 | 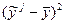 |
| ∑ | ||
| ∑ | Дост | Дрег |
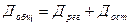
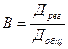
Коэффициент детерминации равный В= характеризует, что ….% изменений величины у вызвано изменением величины х, а (1-В) 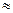 ….% влиянием неучтённых факторов.
….% влиянием неучтённых факторов.
Несмещённая выборочная оценка для дисперсии отклонений случайной величины у от поверхности регрессии вычислим по формуле:
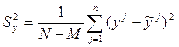
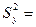
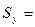
Стандартное отклонение величины у от линии регрессии составляет…., т.е. находится в пределах 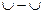 % от значений величины
% от значений величины 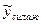 .
.
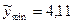
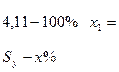
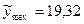
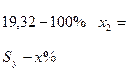 .
.
