Задания для самостоятельного решения
Комплексные числа
Блок №1
Определение комплексного числа. Алгебраическая форма комплексного числа.
Комплексными числами называются упорядоченные пары 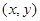 действительных чисел
действительных чисел 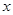 и
и 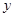 , для которых введены понятия равенства и операции сложения и умножения:
, для которых введены понятия равенства и операции сложения и умножения:
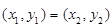 если
если 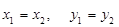 ,
,
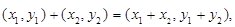
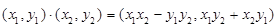 .
.
Комплексные числа вида 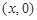 отождествляются с действительными числами
отождествляются с действительными числами 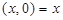 . Особую роль играет число
. Особую роль играет число 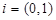 , которое называется мнимой единицей. Заметим, что
, которое называется мнимой единицей. Заметим, что 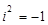 .
.
Каждое комплексное число 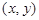 можно представить в виде
можно представить в виде 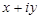 . Такая запись комплексного числа называется алгебраической формой комплексного числа. Число
. Такая запись комплексного числа называется алгебраической формой комплексного числа. Число 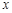 называется действительной частью, а
называется действительной частью, а 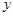 – мнимой частью комплексного числа
– мнимой частью комплексного числа 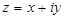 . Для них приняты следующие обозначения:
. Для них приняты следующие обозначения: 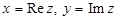 . Комплексное число
. Комплексное число 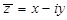 называется сопряженным с комплексным числом
называется сопряженным с комплексным числом 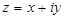 .
.
Вычитание и деление комплексных чисел являются действиями, обратными соответственно сложению и умножению:
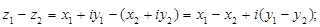
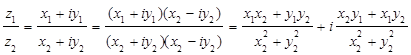
Геометрическое изображение чисел
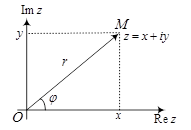 Комплексное число как упорядоченная пара вещественных чисел определяет точку
Комплексное число как упорядоченная пара вещественных чисел определяет точку 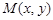 на плоскости или вектор
на плоскости или вектор 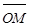 . Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью. Положение точки
. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью. Положение точки 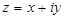 на комплексной плоскости однозначно определяется не только декартовыми координатами
на комплексной плоскости однозначно определяется не только декартовыми координатами 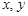 , но и полярными координатами
, но и полярными координатами 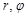 , где
, где 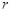 – длина вектора
– длина вектора 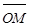 , а
, а 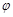 – угол между действительной осью и вектором
– угол между действительной осью и вектором 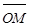 , отсчитываемый от положительного направления действительной оси. При этом, если отсчет ведется против часовой стрелки, то величина угла считается положительной, а если по часовой стрелке – отрицательной. Полярные и декартовы координаты связаны соотношениями
, отсчитываемый от положительного направления действительной оси. При этом, если отсчет ведется против часовой стрелки, то величина угла считается положительной, а если по часовой стрелке – отрицательной. Полярные и декартовы координаты связаны соотношениями 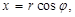
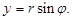
Операциям сложения и вычитания комплексных чисел можно поставить в соответствие операции над векторами:
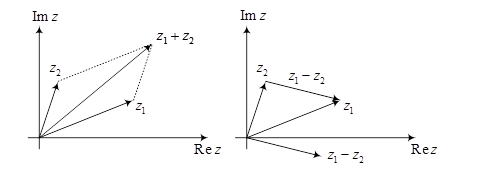
Геометрический смысл разности двух комплексных чисел – это расстояние между точками 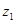 и
и 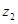 :
: 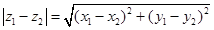 .
.
Задачи
Рассмотрим в аудитории типичные примеры, для решения которых используются приведенные определения, теоремы и понятия:
1.Найти 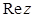 и
и 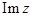 , если
, если
а) 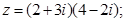 б)
б) 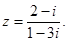
Решение. а) Перемножая почленно и учитывая, что 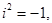 получим:
получим:
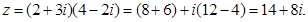
Ответ. 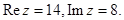
б) Умножим числитель и знаменатель на число, сопряженное знаменателю:
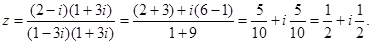
Ответ. 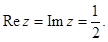
2.Найти 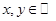 и записать комплексное число
и записать комплексное число 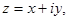 если
если
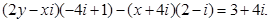
Решение. Выполнив операции над комплексными числами и используя условие
равенства двух комплексных чисел, получим:
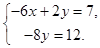 Решаем систему:
Решаем систему: 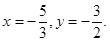
Ответ. 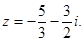
3.Вычислить:
а) 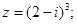 б)
б) 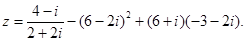
Решение. а) Применяя формулу куба разности, получим:
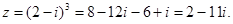
Ответ. 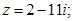
б) Последовательно выполнив операции над комплексными числами,
получим:
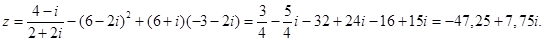
Ответ. 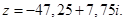
4.Решить уравнение:
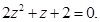
Решение. Находим дискриминант и пару комплексно-сопряженных корней уравнения:
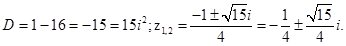
Ответ. 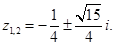
5.Начертить в комплексной плоскости линию, заданную уравнением
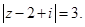
Решение. Так как 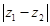 есть расстояние между точками
есть расстояние между точками 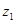 и
и 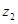 , то из равенства
, то из равенства
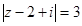 следует, что точки линии удалены от точки
следует, что точки линии удалены от точки 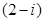 на расстояние,
на расстояние,
равное 3, то есть данная линия – окружность радиуса 3 с центром (2,–1).
Ответ.
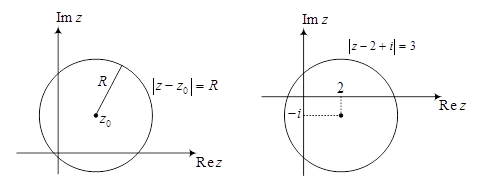
6.Изобразить на комплексной плоскости множество точек, удовлетворяющих заданным неравенствам:
а) 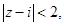 б)
б) 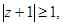 в)
в) 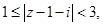
г) 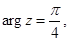 д)
д) 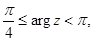 е)
е) 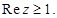
Решение.
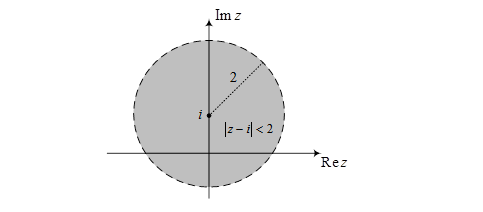
а) Неравенство 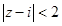 означает, что расстояние от точки
означает, что расстояние от точки 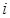 до точек z меньше 2. Этому условию удовлетворяют точки круга с центром в точке
до точек z меньше 2. Этому условию удовлетворяют точки круга с центром в точке 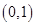 радиуса 2, исключая границу.
радиуса 2, исключая границу.
Ответ.
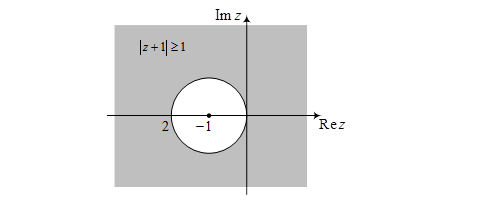
б) Неравенство 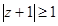 означает, что расстояние от точки
означает, что расстояние от точки 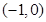 до точек z должно быть не меньше 1. Искомое множество лежит вне круга с центром в точке
до точек z должно быть не меньше 1. Искомое множество лежит вне круга с центром в точке 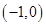 радиуса 1, включая границу.
радиуса 1, включая границу.
Ответ.
в) Искомое множество должно удовлетворять двум неравенствам 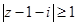 и
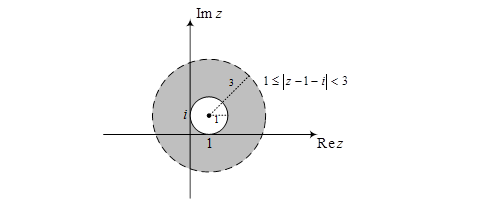
и 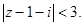 Первое неравенство определяет внешность круга, радиуса 1 с центром в точке (1,1), включая границу. Второе неравенство- круг радиуса 3 с центром в той же точке (1,1), исключая границу. Поэтому данное множество-кольцо с центром в точке (1,1), ограниченное окружностями радиусов
Первое неравенство определяет внешность круга, радиуса 1 с центром в точке (1,1), включая границу. Второе неравенство- круг радиуса 3 с центром в той же точке (1,1), исключая границу. Поэтому данное множество-кольцо с центром в точке (1,1), ограниченное окружностями радиусов 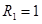 и
и 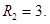
Ответ.
г) Равенство 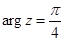 задает на плоскости множество точек с одинаковым аргументом, то есть луч, выходящий из начала координат под углом
задает на плоскости множество точек с одинаковым аргументом, то есть луч, выходящий из начала координат под углом 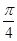 к действительной оси.
к действительной оси.
Ответ.
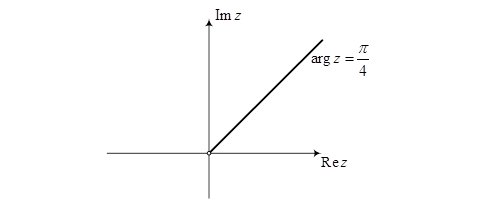
д) Неравенство 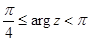 задает на плоскости угол, ограниченный двумя лучами, выходящими из начала координат под углами
задает на плоскости угол, ограниченный двумя лучами, выходящими из начала координат под углами 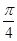 и
и 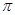 к действительной оси.
к действительной оси.
Ответ.
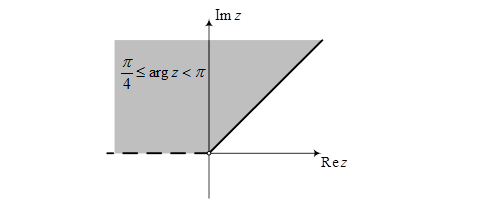
е) Неравенство 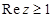 задает на плоскости множество точек, действительная часть которых не меньше 1. Это множество является полуплоскостью с границей, перпендикулярной действительной оси и проходящей через точку (1;0).
задает на плоскости множество точек, действительная часть которых не меньше 1. Это множество является полуплоскостью с границей, перпендикулярной действительной оси и проходящей через точку (1;0).
Ответ.
Задания для самостоятельного решения
1.Найти 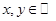 и записать комплексное число
и записать комплексное число 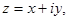 если
если
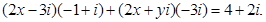
Ответ. 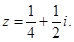
2.Решить систему в комплексных числах:
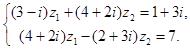
Ответ. 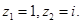
3.Вычислить:
а) 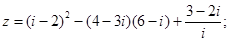
б) 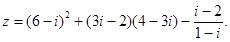
Ответ. 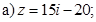
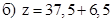 .
.
4.Решить уравнения:
а) 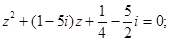 б)
б) 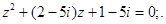
Ответ. 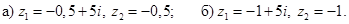
5.Изобразить на комплексной плоскости множество точек, удовлетворяющих неравенствам.
а) 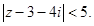
Ответ. Внутренность круга R = 5, центр О(3,4), границы не входят.
б) 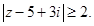
Ответ. Внешность круга R = 2, центр О(5,–3), граница включается.
в) 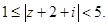
Ответ. Кольцо между двумя окружностями радиусов 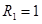 и
и 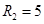 , центр обеих лежит в О(–2,–1). Внешняя окружность не включает границу; внутренняя граница включается.
, центр обеих лежит в О(–2,–1). Внешняя окружность не включает границу; внутренняя граница включается.
г) 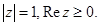
Ответ. Полуокружность 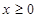 (граница включается).
(граница включается).
Блок №2
