Расчет ректификационных колонн и оптимизация их с помощью ЭВМ
Методика расчета ректификационных колонн на ЭВМ построена на математических методах решения системы уравнений, описывающих процесс разделения. Решение нелинейных уравнений осуществляется методами Тилле и Геддеса или Льюиса—Маттесона. В первом случае независимыми переменными являются температуры и материальные потоки на всех тарелках, во втором — полный состав одного из компонентов. Наибольшее применение в расчетах нашел метод Тилле и Геддеса, где в основу сходимости уравнений положен метод итераций (метод последовательных приближений) или метод Ньютона.
При использовании математической модели, основанной на теоретических тарелках, система балансовых уравнений для заданных по тарелкам значений температур становится линейной относительно составов. В этом случае применяются матричные методы решения систем линейных уравнений с последующей коррекцией распределения температур.
При моделировании процесса ректификации методом числа единиц переноса решение системы уравнений производится способом потарелочного расчета, суть которого состоит в том, что расчет начинают от верха колонны или от кипятильника и выполняют до тех пор, пока на какой-то тарелке полученный состав не будет соответствовать составу исходной смеси — для схем, представленных на рис. 3.1,а, б, или же составу 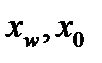 — для схемы по рис. 3.1,в.
— для схемы по рис. 3.1,в.
Рассмотрим расчет числа тарелок по схеме (на рис. 3.1,в в ректификационной колонне для бинарной смеси. При составлении математической модели примем следующие допущения: исходная смесь подается в колонну при температуре кипения; жидкость (пар) на тарелках колонны находится при температуре кипения (насыщения); потоки пара и жидкости, а также давление по высоте секций колонны постоянны; флегма поступает в колонну при температуре кипения; в зоне массообмена на тарелках осуществляется идеальное перемешивание жидкости и идеальное вытеснение пара.
Математическое описание колонны, представленной на рис. 3.3, для разделения бинарной смеси состоит из уравнений общего материального баланса колонны, уравнений материального баланса для произвольного сечения колонны по низкокипящему компоненту и уравнения, описывающего парожидкостное равновесие.
Блок-схема расчета числа тарелок ректификационной колонны приведена на рис. 3.16. Ниже дано описание блоков.
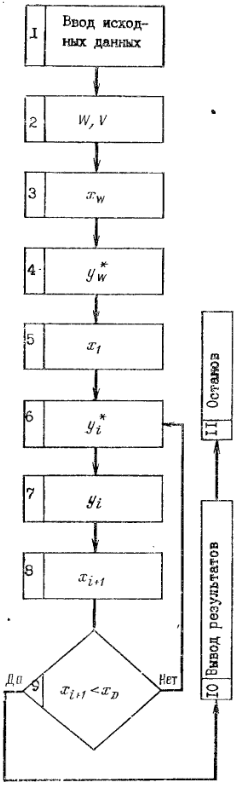
Рис. 3.16 – Блок-схема расчета ректификационной колонны на ЭВМ
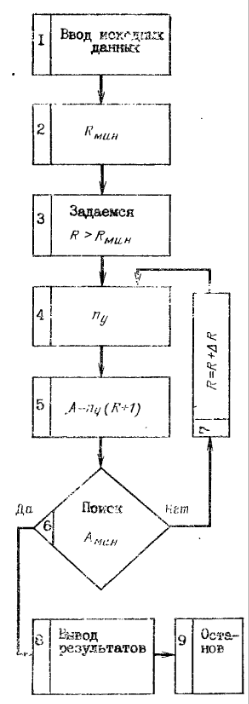
Рис. 3.17 – Блок-схема для определения оптимального флегмового числа 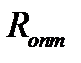 на ЭВМ
на ЭВМ
Блок 1. Исходные данные: F— количество исходного раствора; 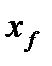 —состав исходного раствора; D—количество отбираемого дистиллята; R— количество подаваемой флегмы; а — коэффициент относительной летучести; xD— состав дистиллята.
—состав исходного раствора; D—количество отбираемого дистиллята; R— количество подаваемой флегмы; а — коэффициент относительной летучести; xD— состав дистиллята.
Б л о к 2. Определение кубового продукта Wи количества пара в колонне V производится по формулам материального баланса:
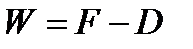 | (3.58) |
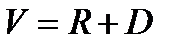 | (3.59) |
Блок 3. Определение xw производится из покомпонентного баланса колонны:
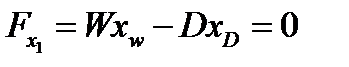 | (3.60) |
Блок 4. Определение равновесного значения концентрации низкокипящего компонента в паровой фазе куба:
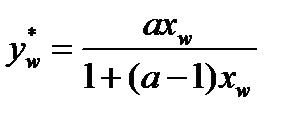 | (3.61) |
Блок 5. Определение состава жидкости 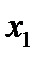 на первой (снизу) тарелке из уравнения материального баланса для куба колонны:
на первой (снизу) тарелке из уравнения материального баланса для куба колонны:
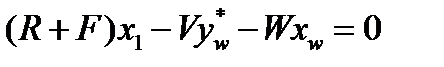 | (3.62) |
Блок 6. Определение равновесного значения концентрации низ- кокипящего компонента 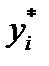 в паровой фазе:
в паровой фазе:
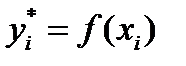 | (3.63) |
которая задается аналитическим выражением, например при постоянстве давления в колонне может быть использовано соотношение (3.61).
Блок 7. Определение состава пара 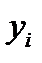 уходящего с i-й тарелки, осуществляется по формуле
уходящего с i-й тарелки, осуществляется по формуле
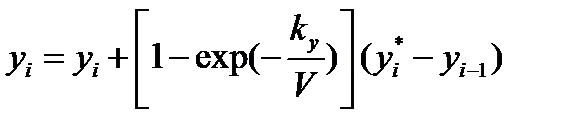 | (3.64) |
где kv— коэффициент массопередачи в паровой фазе.
Блок 8. Определяется состав жидкости на вышерасположен-ной тарелке. Этот блок представляет собой отдельную подпрограмму, в которой при 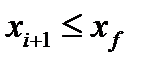 расчет ведут по зависимости (исчерпывающая часть колонны)
расчет ведут по зависимости (исчерпывающая часть колонны)
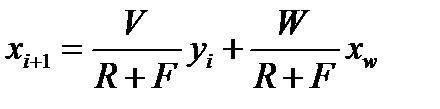 | (3.65) |
При 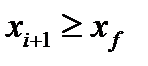 — по зависимости (укрепляющая часть колонны)
— по зависимости (укрепляющая часть колонны)
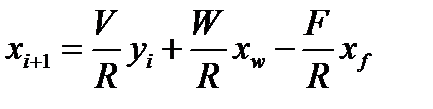 | (3.66) |
Блок 9. Производится проверка величины 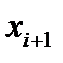 . Если она меньше
. Если она меньше 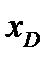 ,то производится расчет состава компонентов на следующей тарелке, если равна или больше, то переходят к блоку 10.
,то производится расчет состава компонентов на следующей тарелке, если равна или больше, то переходят к блоку 10.
Блок 10. Вывод на печать результатов расчета. В тех случаях, когда необходимо рассчитать температуру кипения жидкости как функцию состава на каждой тарелке, систему уравнений математического описания необходимо включить соотношение
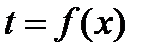 | (3.67) |
Блок 11. Останов, т. е. окончание расчета.
Оптимизация параметров и режимов работы ректификационных колонн приводит к более сложным математическим описаниям, реализация которых осуществляется путем составления отдельных подпрограмм в общем алгоритме расчета колонн.
При проектировании колонн обычно оптимизируют распределение концентраций, температур и давлений по высоте колонны, рабочее флегмовое число; количество подводимой теплоты, эксплуатационные затраты и т. д.
В качестве примера рассмотрим определение оптимального флегмового числа. За основу расчета возьмем метод, предложенный А. Н. Плановским, который основан на наличии пропорциональности между высотой колонны и числом единиц переноса 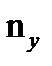 , с одной стороны, и между поперечным сечением колонны и расходом пара, определяемым как (R +1), с другой стороны. Величину оптимального флегмового числа получают из функции
, с одной стороны, и между поперечным сечением колонны и расходом пара, определяемым как (R +1), с другой стороны. Величину оптимального флегмового числа получают из функции
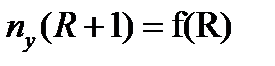 | (3.68) |
Расчет можно производить графически или с помощью ЭВМ. Блок-схема представлена на рис. 3.17. Принята следующая последовательность расчета:
1) Рассчитывается 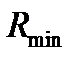 ;
;
2) задается значение 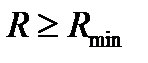 ;
;
3) определяется с помощью уравнений (3.12) и (3.63) подынтегральная функция в уравнении
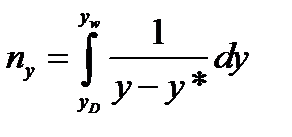 | (3.69) |
определяются пу и A=ny(R+1);
4) производится поиск величины 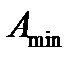 соответствующей
соответствующей 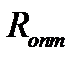 при
при 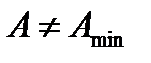 присваивается новое значение R и расчет повторяется.
присваивается новое значение R и расчет повторяется.
Список использованной литературы
1. Александров А.А. Ривкин С.Л. Термодинамические свойства воды и водяного пара: Справочник. М.: Энергоатомиздат, 1984. – 80 с.
2. Дытнерский Ю.И. Основные процессы и аппараты химической технологии. - Москва:1991. – 496 с.
3. Алексеев В.П. Расчет и моделирование аппаратов криогенных установок. Л.: Энергоатомиздат. 1987. – 280 с. Кафаров В.В., Мешалкин В.П., Гурьев Л.В. Оптимизация теплообменных процессов и систем.- М.: Энергоатомиздат, 1988. – 191 с.
4. Павлов К.Ф., Романков П.Г., Носков А.А. Примеры и задачи по курсу процессы и аппараты химической технологии. 10-е изд., перераб. и доп. - Ленинград: Химия. 1987. – 576 с.
5. Соболь Б.В., Месхи Б.Ч., Каныгин Г.И. Методы оптимизации. Практикум. Высшее образование. И.: Феникс, 2009. – 384 с.
6. Шервуд Т. Пигфорд Р. Уилки Ч. Массопередача. М.: 1982. – 696 с.
