Устойчивость устройств с обратной связью

Обеспечение устойчивости является необходимым условием правильного выполнения устройством задач по обработке сигнала.

Можно выделить три формы проявления неустойчивости:

· наличие сигнала на выходе устройства при отсутствии внешних источников сигнала;

· повышенный уровень шумоподобного сигнала и нелинейных искажений;

· неустойчивость при подаче входного сигнала.

На рис. 3.7 представлена зависимость амплитуды выходного синусоидального сигнала U_{ВЫХ max} от амплитуды входного синусоидального сигнала U_{ВХ max}.

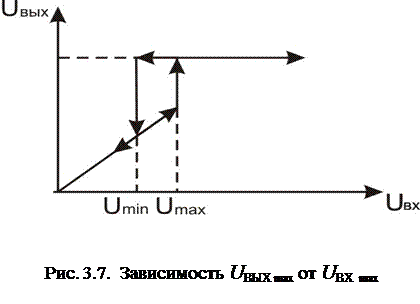При малом входном сигнале наблюдается увеличение выходного сигнала, пропорциональное входному. При достижении входным сигналом значения U_max наблюдается скачкообразное увеличение выходного сигнала. При дальнейшем увеличении входного сигнала уровень выходного сигнала сохраняется постоянным.

При обратном уменьшении входного сигнала уровень выходного сигнала не изменяется до тех пор, пока входной сигнал не достигнет значения U_min. При достижении этого значения уровень выходного сигнала скачкообразно уменьшится, и при дальнейшем уменьшении входного сигнала выходной сигнал пропорционально уменьшится.

Таким образом, в реальных устройствах устойчивость зависит от величины входного сигнала.

Устройства, у которых не наблюдаются первые две формы неустойчивости, называются устойчивыми в малом. Устройства, у которых отсутствует третья форма неустойчивости, называются устойчивыми в большом, или устойчивыми в режиме вынужденных колебаний.

Пусть схема устройства содержит n узлов и до момента времени t₀ узловые напряжения имеют значения U_i(t₀) = U_i(0), t < t₀. Пусть в момент времени t₀ ко всем узлам будет приложен импульсный скачок напряжения ∆U_i δ(t) = ∆U_i (0).

Устройство называется устойчивым по Ляпунову, если по 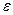>0 можно указать такое 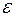> 0, что как только выполняется условие

,

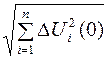
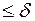немедленно выполняется условие

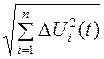
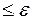для t > t ₀.

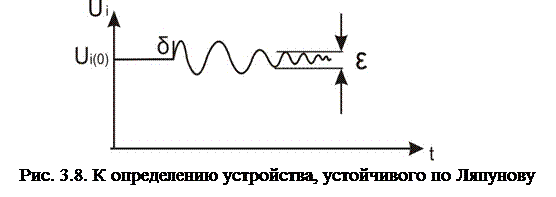
Устойчивость по Ляпунову иллюстрирует рис. 3.8 на примере одного узла.

Устройство называется асимптотически устойчивым, если оно устойчиво по Ляпунову и выполняется условие

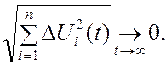
Устройство называется асимптотически устойчивым в целом, если оно асимптотически устойчиво при любых отклонениях начальных условий ∆U_i (t₀).

Сформулированные выше устойчивости в малом и большом есть частные случаи устойчивости по Ляпунову.

Проектируемое устройство должно удовлетворять третьему определению устойчивости, так как только в этом случае при скачкообразном отклонении начальных условий в виде короткого импульса устройство возвращается в первоначальное состояние при любых значениях отклонений.

Для того, чтобы выяснить, является ли устройство устойчивым, необходимо сформулировать критерии устойчивости, т.е. признак того, что выполняются условия устойчивости, данные в определениях.

Линейные устройства описываются передаточной функцией T(p) = 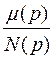, где р - оператор Лапласа, 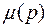- алгебраический полином степени m, N(p) - характеристический полином устройства степени m. Для линейного устройства сформулирован следующий алгебраический критерий: устройство является устойчивым по Ляпунову, если степень числителя T (p) не превосходит степени знаменателя, т.е. m ≤ n , и все корни характеристического полинома N(p) лежат в левой p-полуплоскости.

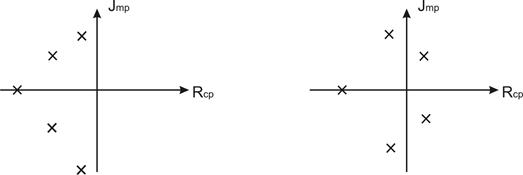
На рис. 3.9,а изображена p-плоскость и возможное расположение корней устойчивого устройства, имеющего характеристический полином пятой степени.

Рис. 3.9,б иллюстрируeт расположение корней неустойчивого устройства, полином N(p) которого имеет пару комплексно-сопряженных корней, расположенных в правой p-полуплоскости.

	а)		б)

Рис. 3.9. Корни полиномов устойчивого (а) и неустойчивого (б) устройства

Существует еще несколько алгебраических критериев (Льенара-Шепара, Раусса-Гурвица и др.), которые по специальным правилам проверяют определитель матриц, составляемых из коэффициентов полинома N(p).

Область применения алгебраических критериев устойчивости ограничена устройствами, для которых степень полинома N(p), т.е. число реактивных элементов лежит в пределах n = 2÷5. К таким объектам относятся простейшие системы авторегулирования. Степень полинома N(p) реальных устройств (фильтры, корректоры, усилители) может достигать значений n = 20÷50. Для этих значений точное определение коэффициентов полинома N(p) и его корней является сложной, а иногда невыполнимой вычислительной задачей даже для современных вычислительных средств.

Кроме того, алгебраические критерии работают с моделями устройства, т.е. с его математическим описанием. В ряде случаев само устройство, либо его отдельные части могут не иметь адекватного математического описания.

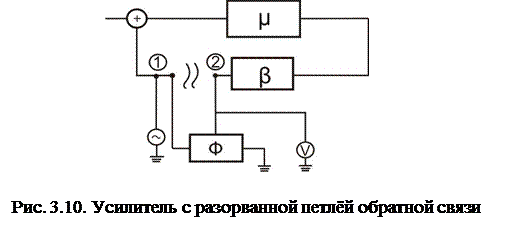
В связи с этим возникает необходимость сформулировать такой критерий устойчивости, который бы использовал результаты измерений характеристик самого устройства. Прежде чем перейти к этому критерию, дадим определение понятия годограф вектора.

Следуя рис. 3.10, разорвем петлю обратной связи, подсоединим к первой точке разрыва генератор синусоидального сигнала, ко второй точке разрыва подсоединим вольтметр V и фазометр Ф. Для частоты ω измерим значение

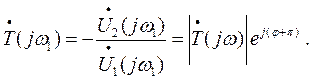
На рис. 3.11 изображена комплексная плоскость величины 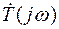, а на ней – векторы 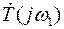, , 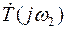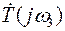и т. д. для различных частот.

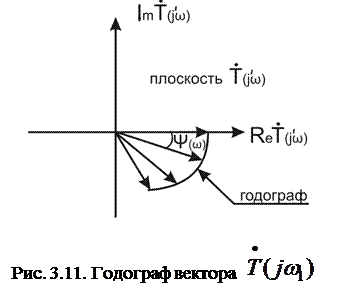
Длина вектора равна модулю 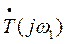, а угол 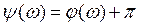, где 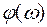– угол, измеренный фазометром Ф. Угол π появляется вследствие того, что возвратное отношение 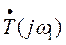, по определению, противоположно по знаку усилению по петле обратной связи, измеряемому в соответствии с рис. 3.10.

Годографом вектора 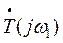называется кривая, соединяющая концы векторов 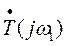для различных частот. Сформулируем частотный критерий Найквиста для устройства с одноканальной обратной связью.

Пусть устройство без обратной связи устойчиво. Для того, чтобы устройство при введении обратной связи было асимптотически устойчиво в целом, необходимо и достаточно, чтобы годограф вектора 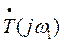не охватывал точку (– 1, 0) на плоскости 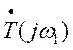, т.е. число пересечений оси 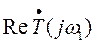слева от точки (– 1, 0) было бы четным.

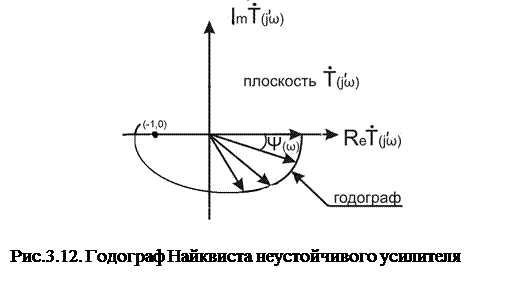
На рис. 3.12 представлен годограф Найквиста неустойчивого усилителя с ОС; годограф вектора 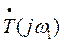охватывает точку (– 1,0).

Варианты диаграмм с годографом Найквиста устойчивых усилителей с ОС изображены на рис. 3.13,а , 3.13,б.

Устройство, имеющее форму годографа 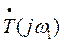, представленную на рис. 3.13,а, и имеющее четное (два) число пересечений оси абсцисс слева от точки (– 1, 0), называется устойчивым по Найквисту. Устройство, иллюстрируемое рис. 3.13,б, имеет ноль, т.е. четное число пересечений слева от точки (– 1, 0), и называется устойчивым по Боде.

а)	б)
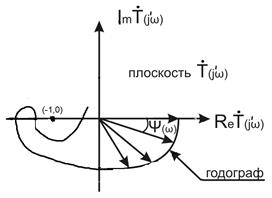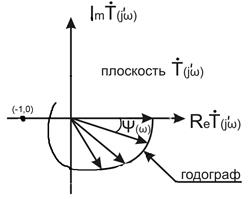Рис.3.13. Годографы Найквиста: а - усилитель устойчив по Найквисту; б - усилитель устойчив по Боде

Критерий Найквиста справедлив для линейных и нелинейных устройств с ОС и является конструктивным. Он не только решает задачу анализа устойчивости, но и позволяет спроектировать заведомо устойчивое устройство, формируя требуемую диаграмму Найквиста с помощью корректирующих цепей, включаемых в 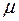- канал прямой передачи.

Вместе с тем, применение критерия Найквиста имеет ряд ограничений:

· критерий Найквиста был создан в эпоху ламповой схемотехники, когда каскады усилителя имели как правило трансформаторную связь. В современных условиях в большинстве случаев транзисторные каскады имеют прямую гальваническую связь, разрыв цепи ОС может нарушить режим работы усилителя по постоянному току;

· сегодня во многих случаях невозможен доступ к желаемой точке разрыва цепи ОС, например, при исполнении усилителя в виде ИМС;

· реальная схема усилителя может иметь несколько каналов ОС, а критерий Найквиста предполагает наличие в усилителе одноканальной ОС.

В [8] предложен и реализован метод определения неустойчивости усилителя без разрыва цепи ОС. Вопрос об устойчивости или неустойчивости усилителя решается анализом характеристики группового времени распространения (ГВР) от входа до выхода усилителя без размыкания цепи ОС. ГВР – это производная первого порядка от ФЧХ по круговой частоте, взятая со знаком минус. Достаточным условием возникновения неустойчивости усилителя является наличие на оси частот участка с отрицательным значением ГВР.

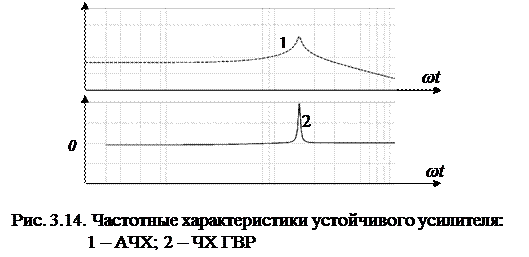
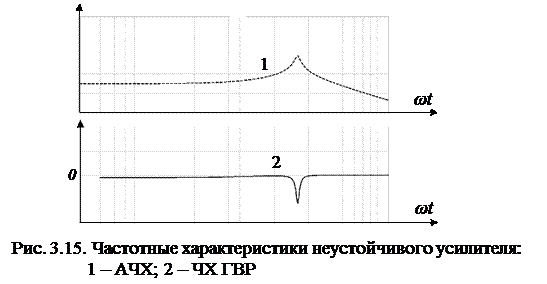
Примеры частотных характеристик устойчивого и неустойчивого усилителя приведены соответственно на рис. 3.14 и рис. 3.15. Характер АЧХ у данных усилителей абсолютно идентичен и не несёт информации об устойчивости или неустойчивости усилителя. В то же время характер ЧХ ГВР весьма информативен – у неустойчивого усилителя (рис. 3.15) имеется явно выраженный отрицательный участок на графике 2.