Існування кореня многочлена над довільним полем. Формули Вієта.

Наведемо приклади многочленів над полем Р, які не мають жодного корення у цьому полі.

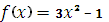над полем Q не має рац. коренів. Многочлен 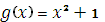над полем R не має дійсних коренів. Але кожній з цих многочленів має корені в деякому розширенні розглядуваного поля, а саме: 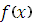має корені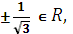 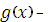корені .

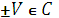Теорема 3 (Кронекера): Якщо 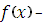довільний многочлен над полем Р, для якого 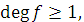то існує розширення К поля Р, в якому є корінь .

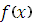Теорема 4: Для будь-якого многочлена 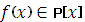степеня 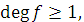існує таке розширення L поля Р, в якому 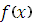розкладається на лінійні множники.

Означення 1:Поле L, в якому многочлен 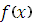розкладається на лінійні многочлени, називають полем розкладу цього многочлена.

Приклад 1.

не розкладається на множники 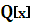в.

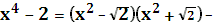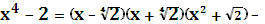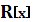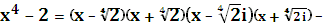
в кінці многочленів над полем чисел виду в кінці многочленів над полем R дійсних чисел 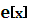над полем дійсних чисел, всі множники лінійні, тому С поле розкладу.

Означення 2:Поле Р називається алгебраїчно замкнутим, якщо воно є полем розкладу для будь-якого многочлена 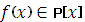ненульового степеня.

Приклад:поле С комплексних чисел. Твердження про алгебраїчну замкненість цього поля основна теорема теорії многочленів.

Наслідок 1:Многочлен 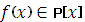n-го степеня має у полі розкладу n коренів.

Наслідок 2:У полі розкладу многочлен 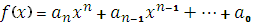має канонічний розклад виду 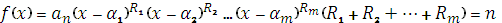, де 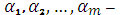різні корені многочлена .

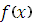Теорема 5 (Вієта):Якщо 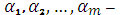корені многочлена 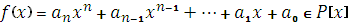, то

,

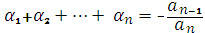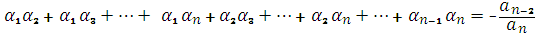, (3)

……………………………………………………………………………………

…………………………………………………………………………………….

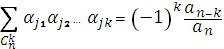
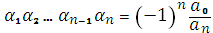
Символ 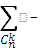cлід тут розмістити так, що сума береться по всіх 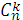комбінаціях з n індексів 1,2,3,…, n по k.

Для доведення формул (3) досить виконати множення у правій частині рівності:

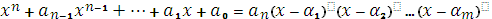
Формули Вієта.

Ф. Вієт (1540-1603) видатний французький математик.

4.Про алгебраїчну і функціональну рівність многочленів.

Приклади.

Алгебраїчна рівність:

Означення 1: Многочлени 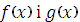називають рівними між собою і записують 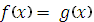, якщо канонічні форми цих многочленів збігаються: тобто .

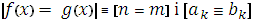Нехай 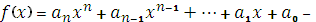многочлен над областю цілісності R, а С – деяке комутативне кільце що є розширенням R. Якщо α – будь-який елемент з С то має сенс вираз:

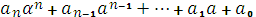, бо в (1) С визначено дії множення і додавання над елементами α, 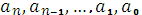. Вираз (1) утворений з 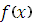заміного символа х елементом α. Позначають f(α) і називають значенням многочлена f(х) при х=α.

Кожному 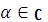відповідає за цим правилом єдиний елемент f(α) .

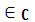Теорема 2: Якщо f(х) — будь-який многочлен над областю цілісності R, а С – деяке комутативне кільце, яке є розширенням R, то поставивши кожному елементу 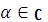у відповідність елемент f(α) 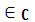, дістаємо функцію .

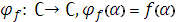Наслідок : Якщо R — область цілісності, що є числовим полем , то многочлени рівні між собою тоді і тільки тоді, коли їх значення в довільний точці області R рівні між собою.

*******************************************************************************

Лекція 4

Кратні множники многочлена

План.

1. Похідна многочлена. Властивості. Схема обчислення похідних в точці.

2. Незвідні кратні множники многочлена.

3. Задача відокремлення кратних множників.

4. Ознака кратності кореня многочлена.

1.Похідна многочлена. Властивості. Схема обчислення похідних в точці.

Похідною .від многочлена f’(x)=na_nx^n-1+(n-1)a_n-1x^n-2+…+2a₂x +a₁(*).

Похідна від многочлена нульового степеня, а також похідну від нуль-многочлена беруть рівною нулю.

Похідна від многочлена над полем Р є знову многочлен над полем Р.

Будемо розглядати многочлени та їх похідні над полем дійсних чисел.

deg f’=degf-1.

Для многочленів над полем дійсних чисел(як і для диференційованих функції) справедливі, як відомо, такі правила диференціювання:

[f(x)+g(x)]’=f’(x)+g’(x) (1)

[f(x)*g(x)]’=f’(x)g(x)+f(x)g’(x) (2)

І, зокрема,

[cf(x)]’=cf’(x) – (c - константа) (3)

Справедливість цих рівностей не залежить від того, над яким полем ці многочлени розглядають, бо вони означають просто рівність відповідних коефіцієнтів многочленів в обох частинах рівностей.

Пояснимо цю думку на прикладі формули (1). Якщо дано два многочлена з кільця R[x]:

f(x)=a_nxⁿ +a_n-1x^n-1+…+a₁x+a_0,

g(x) = b_mx^m +b_m-1x^m-1+…+b₁x+b_0, (n≥m), то

f(x)+g(x)= a_nxⁿ +a_n-1x^n-1+…+(a_m+b_m)x^m+…+(a₁+b₁)x+(a₀+b₀).

Переходячи до похідних за правилом (*), помічаємо, що формула (1) означає просто тотожну рівність многочленів:

na_nx^n-1+(n-1)a_n-1x^n-2+…+m(a_m+b_m)_x^m-1+…+(a₁+b₁)= [na_nx^n-1+(n-1)a_n-1x^n-2+…+ma_mx^m-1+…+a₁] +[mb_mx^m-1+…+b₁](4)

Можна розглядати f’(x), f’’(x), f’’’(x),…f^k(x). При цьому f^k(x) – визначають як похідну f^(k+1)x, f^k(x)=0, k>n, fⁿ(x)=n!a_n(a_n – сталий коефіцієнт f(x)).

2.Незвідні кратні множники многочлена.

Всякий многочлен над полем Р можна єдиним способом подати у вигляді добутку многочленів нижніх степенів, незвідних у цьому полі:

f(x)=[p₁(x)]^k1[p₂(x)]^k2…[p_i(x)]^ki (5)

Якби для кожного многочлена був відомий канонічний розклад (5), тоді було б досить розглядати лише незвідні множники, степінь яких, як правило, значно нижчий за степінь даного многочлена.

Покажемо, що в деяких випадках можливо розробити загальний метод розкладання многочлена на множники, хоч цей розклад не буде таким повним, як зображення (5).

Виберемо у розкладі (5) ті незвідні множники p_i(x), кратність яких k_i дорівнює 1, і позначимо добуток цих множників через µ₁(x):

µ₁(x)=p_i1(x) p_i2(x)… p_is(x)

Тепер утворимо добуток тих множників p_j(x) – кратність яких k_j =2, тобто тих, які входять у (5)зі степенем 2.

µ₂(x)=p_j1(x) p_j2(x)… p_js(x)

µ₂(x) – добуток самих незвідних множників, а не їх квадратів, так що в розклад входить [µ₂(x)]².

µ₃(x) – добуток незвідних множників кратності 3 і т.д.

Розклад (5) можна записати:

f(x)= µ₁(x)[ µ₂(x)]²[ µ₃(x)]³…[ µ_m(x)]^m, (6)

або ж f= µ₁ µ₂² µ₃³... µ_m^m.

Якщо множників кратності k<m в розкладі (6) немає природно вважають µ_k=1.

Розклад (6) доцільний тоді, коли в (5) існують кратні множники. Якщо ні, то f(x)= µ₁ (x).

Приклад 1.

f(x)= x¹³-5x¹²+6x¹¹+4x¹⁰-9x⁹+5x⁸-6x⁷-4x⁶+8x⁵=x⁵(x-2)³(x²+1)(x+1)²(x-1).

µ₁=(x²+1)(x-1)=x³-x²+x-1, µ₂=x+1, µ₃=x-2, µ₄=1, µ₅=5.

f(x)= µ₁(x)*[ µ₂(x)]²*[ µ₃(x)]³*[ µ₄(x)]⁴*[ µ₅(x)]⁵.

В цьому прикладі розклад многочлена f(x) на множники µ_k(x) дає змогу повністю знайти всі його корені, тому , що ми вміємо розв’язувати рівняння 1-3 степенями.

№3