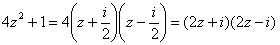Задания для самостоятельного решения
Задание.
А1. Найти: 1. 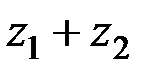 ; 2.
; 2. 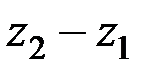 ; 3.
; 3. 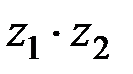 ;4.
;4.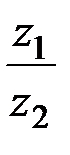 .
.
1.1 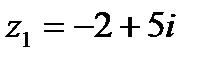 и и 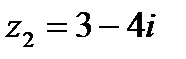 | 1.2 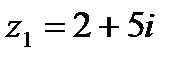 и и 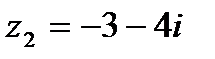 |
1.5 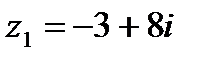 и и 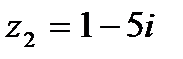 | 1.6 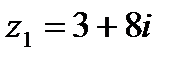 и и 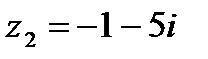 |
1.9 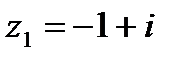 и и 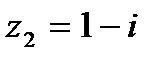 | 1.10 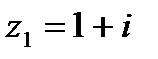 и и 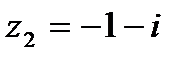 |
1.13 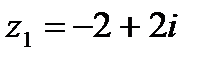 и и 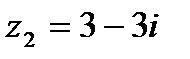 | 1.14 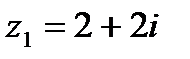 и и 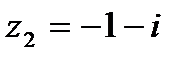 |
1.17 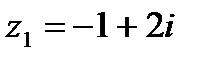 и и 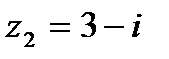 | 1.18 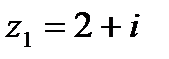 и и 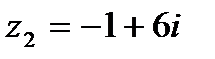 |
1.21 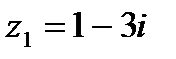 и и 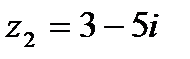 | 1.22 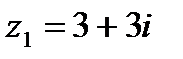 и и 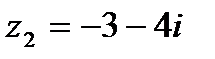 |
1.25 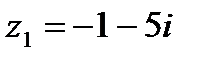 и и 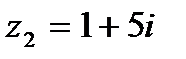 | 1.26 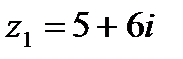 и и 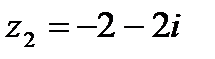 |
1.29 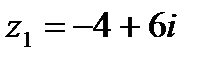 и и 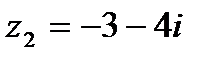 | 1.30 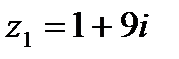 и и 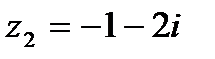 |
1.3 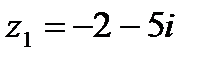 и и 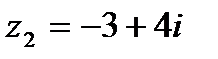 | 1.4 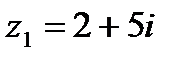 и и 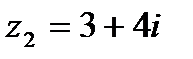 |
1.7 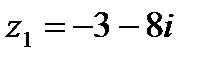 и и 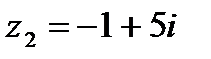 | 1.8 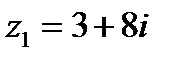 и и 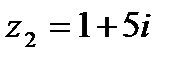 |
1.11 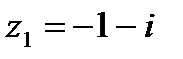 и и 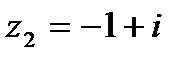 | 1.12 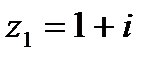 и и 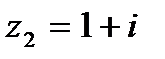 |
1.15 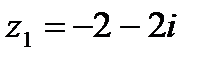 и и 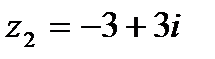 | 1.16 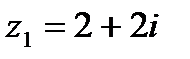 и и 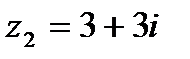 |
1.19 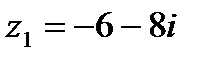 и и 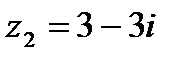 | 1.20 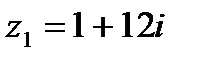 и и 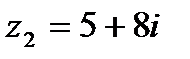 |
А2. Представить в тригонометрической и показательной форме комплексные числа:
1.1 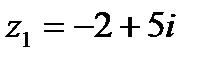 и и 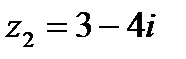 | 1.2 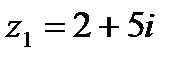 и и 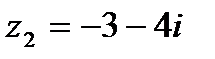 |
1.5 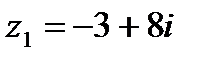 и и 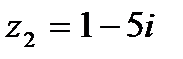 | 1.6 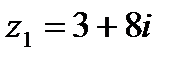 и и 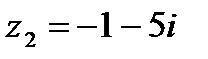 |
1.9 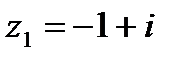 и и 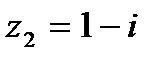 | 1.10 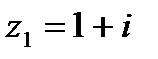 и и 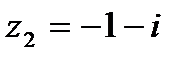 |
1.13 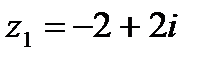 и и 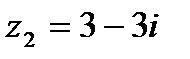 | 1.14 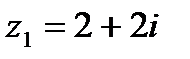 и и 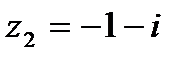 |
1.17 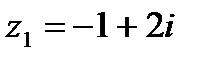 и и 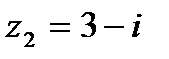 | 1.18 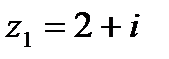 и и 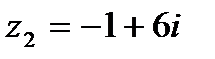 |
1.21 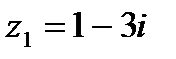 и и 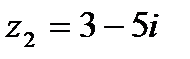 | 1.22 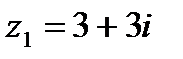 и и 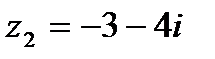 |
1.25 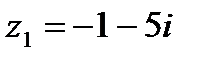 и и 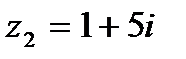 | 1.26 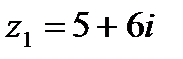 и и 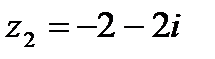 |
1.29 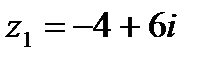 и и 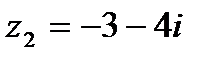 | 1.30 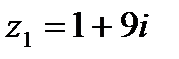 и и 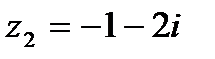 |
1.3 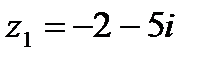 и и 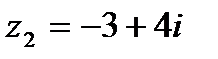 | 1.4 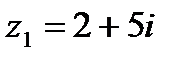 и и 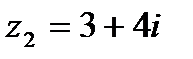 |
1.7 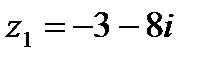 и и 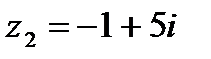 | 1.8 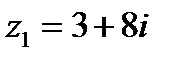 и и 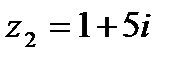 |
1.11 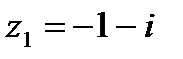 и и 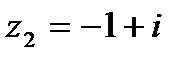 | 1.12 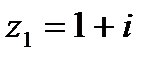 и и 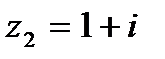 |
1.15 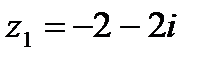 и и 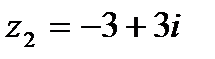 | 1.16 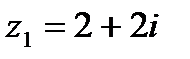 и и 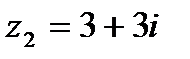 |
1.19 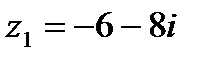 и и 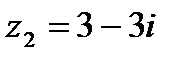 | 1.20 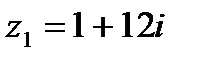 и и 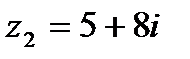 |
А3. Возвести в степень (формула Муавра):
1.1 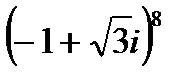 | 1.2 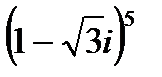 | 1.3 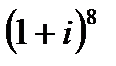 | 1.4 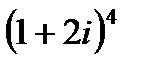 |
1.5 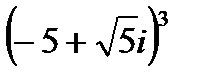 | 1.6 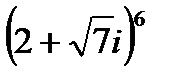 | 1.7 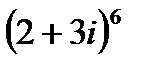 | 1.8 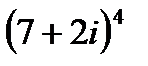 |
1.9 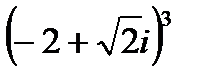 | 1.10 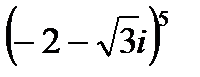 | 1.11 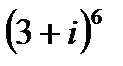 | 1.12 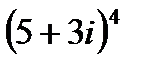 |
1.13 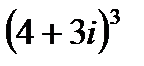 | 1.14 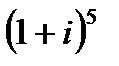 | 1.15 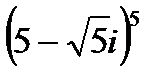 | 1.16 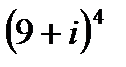 |
1.17 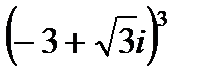 | 1.18 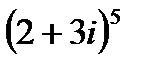 | 1.19 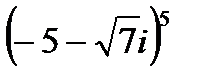 | 1.20 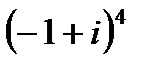 |
1.21 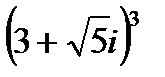 | 1.22 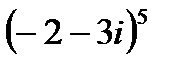 | 1.23 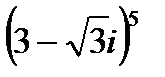 | 1.24 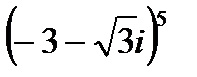 |
1.25 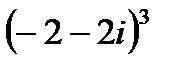 | 1.26 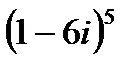 | 1.27 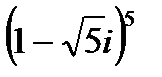 | 1.28 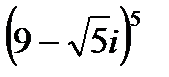 |
1.29 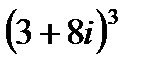 | 1.30 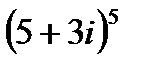 |
А4. Решить уравнение:
1.1 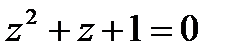 | 1.2 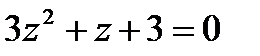 | 1.3 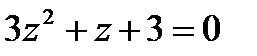 | 1.4 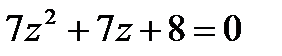 |
1.5 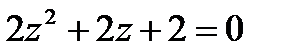 | 1.6 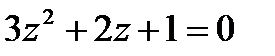 | 1.7 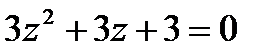 | 1.8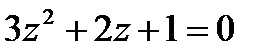 |
1.9 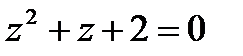 | 1.10 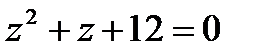 | 1.11 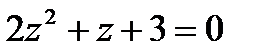 | 1.12 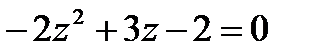 |
1.13 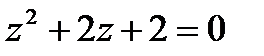 | 1.14 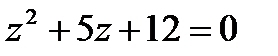 | 1.15 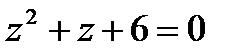 | 1.16 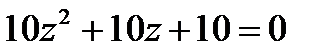 |
1.17 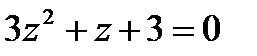 | 1.18 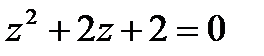 | 1.19 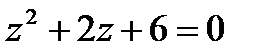 | 1.20 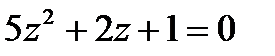 |
1.21 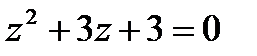 | 1.22 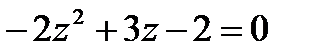 | 1.23 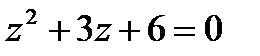 | 1.24 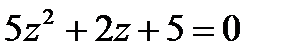 |
1.25 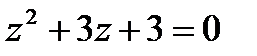 | 1.26 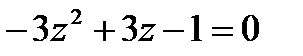 | 1.27 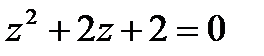 | 1.28 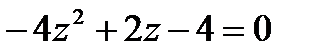 |
1.29 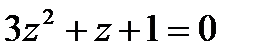 | 1.30 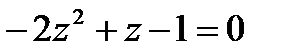 |
Контрольные вопросы по теме
1.Какие числа называются комплексными?
2.Что называется действительной частью комплексного числа?
3.Что называется мнимой частью комплексного числа?
4.Какая форма записи комплексного числа называется алгебраической?
5.Какая форма записи комплексного числа называется тригонометрической?
6.Какая форма записи комплексного числа называется показательной?
7.Что такое Arg z?
8.Чему равен Arg z для внутренних точек I и IV четвертей?
9.Чему равен Arg z для внутренних точек II четверти?
10.Чему равен Arg z для внутренних точек III четверти?
Практическое занятие № 10
Тема:Действия над комплексными числами в тригонометрической и показательной формах.
Цель: отработка умений и навыков выполнения действий над комплексными
числами, заданными в тригонометрической и показательной формах.
Задачи:
• развитие творческого профессионального мышления;
• познавательная мотивация;
• овладение языком науки, навыки оперирования понятиями;
• овладение умениями и навыками постановки и решения задач;
• углубление теоретической и практической подготовки;
• развитие инициативы и самостоятельности студентов.
Обеспечение практического занятия:
Теоретический материал методической рекомендации к практической работе.
Учебник. Богомолов Н.В. «Математика». – М.: Дрофа, 2009.
Индивидуальные карточки с вариантом практической работы.
Ход практического занятия.
1.Формулирование темы занятия, пояснение связи темы с другими темами учебной дисциплины;
2.Проверка готовности студентов к занятию;
3.Проведение непосредственно занятия согласно тематике и в соответствии с рабочей программой дисциплины:
›Изучить теоретический материал по теме «Действия над комплексными числами в тригонометрической и показательной формах».
›Рассмотреть примеры решения типовых заданий.
›Выполнить самостоятельную работу №4.
›Ответить на контрольные вопросы.
Теоретические сведения и методические рекомендации
По решению задач.
Комплексное число — это выражение вида a + bi, где a, b — действительные числа, а i — так называемая мнимая единица, символ, квадрат которого равен –1, то есть i2 = –1. Число a называется действительной частью, а число b — мнимой частью комплексного числа z = a + bi. Если b = 0, то вместо a + 0i пишут просто a. Видно, что действительные числа — это частный случай комплексных чисел.
Арифметические действия над комплексными числами те же, что и над действительными: их можно складывать, вычитать, умножать и делить друг на друга. Сложение и вычитание происходят по правилу (a + bi) ± (c + di) = (a ± c) + (b ± d)i, а умножение — по правилу (a + bi) · (c + di) = (ac – bd) + (ad + bc)i (здесь как раз используется, что i2 = –1). Число 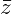 = a – bi называется комплексно-сопряженным к z = a + bi. Равенство z ·
= a – bi называется комплексно-сопряженным к z = a + bi. Равенство z · 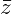 = a2 + b2 позволяет понять, как делить одно комплексное число на другое (ненулевое) комплексное число:
= a2 + b2 позволяет понять, как делить одно комплексное число на другое (ненулевое) комплексное число:
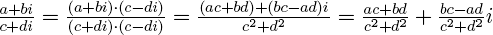 .
.
(Например, 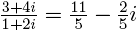 .)
.)
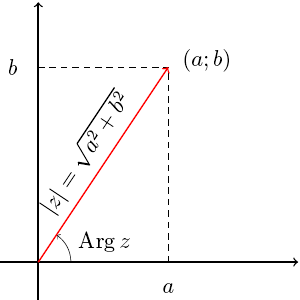 У комплексных чисел есть удобное и наглядное геометрическое представление: число z = a + bi можно изображать вектором с координатами (a; b) на декартовой плоскости (или, что почти то же самое, точкой — концом вектора с этими координатами). При этом сумма двух комплексных чисел изображается как сумма соответствующих векторов (которую можно найти по правилу параллелограмма). По теореме Пифагора длина вектора с координатами (a; b) равна
У комплексных чисел есть удобное и наглядное геометрическое представление: число z = a + bi можно изображать вектором с координатами (a; b) на декартовой плоскости (или, что почти то же самое, точкой — концом вектора с этими координатами). При этом сумма двух комплексных чисел изображается как сумма соответствующих векторов (которую можно найти по правилу параллелограмма). По теореме Пифагора длина вектора с координатами (a; b) равна 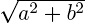 . Эта величина называется модулем комплексного числа z = a + bi и обозначается |z|. Угол, который этот вектор образует с положительным направлением оси абсцисс (отсчитанный против часовой стрелки), называется аргументом комплексного числа z и обозначается Arg z. Аргумент определен не однозначно, а лишь с точностью до прибавления величины, кратной 2π радиан (или 360°, если считать в градусах) — ведь ясно, что поворот на такой угол вокруг начала координат не изменит вектор. Но если вектор длины r образует угол φ с положительным направлением оси абсцисс, то его координаты равны (r · cos φ; r · sin φ). Отсюда получается тригонометрическая форма записи комплексного числа: z = |z| · (cos(Arg z) + i sin(Arg z)). Часто бывает удобно записывать комплексные числа именно в такой форме, потому что это сильно упрощает выкладки. Умножение комплексных чисел в тригонометрической форме выглядит очень просто: z1 · z2 = |z1| · |z2| · (cos(Arg z1 + Arg z2) + i sin(Arg z1 + Arg z2)) (при умножении двух комплексных чисел их модули перемножаются, а аргументы складываются). Отсюда следуют формулы Муавра: zn = |z|n · (cos(n · (Arg z)) + i sin(n · (Arg z))). С помощью этих формул легко научиться извлекать корни любой степени
. Эта величина называется модулем комплексного числа z = a + bi и обозначается |z|. Угол, который этот вектор образует с положительным направлением оси абсцисс (отсчитанный против часовой стрелки), называется аргументом комплексного числа z и обозначается Arg z. Аргумент определен не однозначно, а лишь с точностью до прибавления величины, кратной 2π радиан (или 360°, если считать в градусах) — ведь ясно, что поворот на такой угол вокруг начала координат не изменит вектор. Но если вектор длины r образует угол φ с положительным направлением оси абсцисс, то его координаты равны (r · cos φ; r · sin φ). Отсюда получается тригонометрическая форма записи комплексного числа: z = |z| · (cos(Arg z) + i sin(Arg z)). Часто бывает удобно записывать комплексные числа именно в такой форме, потому что это сильно упрощает выкладки. Умножение комплексных чисел в тригонометрической форме выглядит очень просто: z1 · z2 = |z1| · |z2| · (cos(Arg z1 + Arg z2) + i sin(Arg z1 + Arg z2)) (при умножении двух комплексных чисел их модули перемножаются, а аргументы складываются). Отсюда следуют формулы Муавра: zn = |z|n · (cos(n · (Arg z)) + i sin(n · (Arg z))). С помощью этих формул легко научиться извлекать корни любой степени 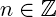 из комплексных чисел. Корень n-й степени из числа z — это такое комплексное число w, что wn = z. Видно, что
из комплексных чисел. Корень n-й степени из числа z — это такое комплексное число w, что wn = z. Видно, что 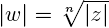 , а
, а 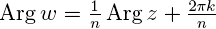 , где k может принимать любое значение из множества {0, 1, ..., n – 1}. Это означает, что всегда есть ровно n корней n-й степени из комплексного числа (на плоскости они располагаются в вершинах правильного n-угольника).
, где k может принимать любое значение из множества {0, 1, ..., n – 1}. Это означает, что всегда есть ровно n корней n-й степени из комплексного числа (на плоскости они располагаются в вершинах правильного n-угольника).
Любое комплексное число (кроме нуля) 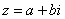 можно записать в тригонометрической форме:
можно записать в тригонометрической форме:
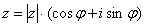 , где
, где 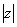 – это модуль комплексного числа, а
– это модуль комплексного числа, а 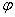 – аргумент комплексного числа.
– аргумент комплексного числа.
Изобразим на комплексной плоскости число 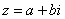 . Для определённости и простоты объяснений расположим его в первой координатной четверти, т.е. считаем, что
. Для определённости и простоты объяснений расположим его в первой координатной четверти, т.е. считаем, что 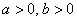 :
:
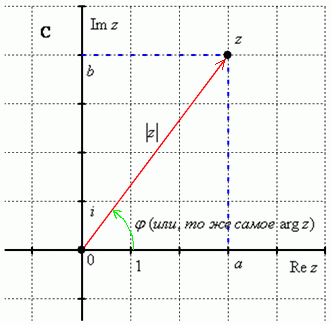
Модулем комплексного числа 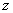 называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длина радиус-вектора, который на чертеже обозначен красным цветом.
называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длина радиус-вектора, который на чертеже обозначен красным цветом.
Модуль комплексного числа 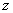 стандартно обозначают:
стандартно обозначают: 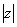 или
или 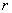
По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: 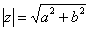 . Данная формула справедлива для любых значений «а» и «бэ».
. Данная формула справедлива для любых значений «а» и «бэ».
Примечание: модуль комплексного числа представляет собой обобщение понятиямодуля действительного числа, как расстояния от точки до начала координат.
Аргументом комплексного числа 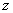 называется угол
называется угол 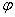 между положительной полуосью действительной оси
между положительной полуосью действительной оси 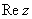 и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа:
и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: 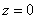 .
.
Аргумент комплексного числа 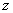 стандартно обозначают:
стандартно обозначают: 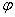 или
или 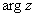
Из геометрических соображений получается следующая формула для нахождения аргумента:
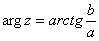 . Внимание! Данная формула работает только в правой полуплоскости! Если комплексное число располагается не в 1-ой и не 4-ой координатной четверти, то формула будет немного другой. Эти случаи мы тоже разберем.
. Внимание! Данная формула работает только в правой полуплоскости! Если комплексное число располагается не в 1-ой и не 4-ой координатной четверти, то формула будет немного другой. Эти случаи мы тоже разберем.
Но сначала рассмотрим простейшие примеры, когда комплексные числа располагаются на координатных осях.
Пример 1.
Представить в тригонометрической форме комплексные числа: 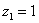 ,
, 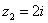 ,
, 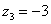 ,
, 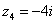 .
.
Выполним чертёж:
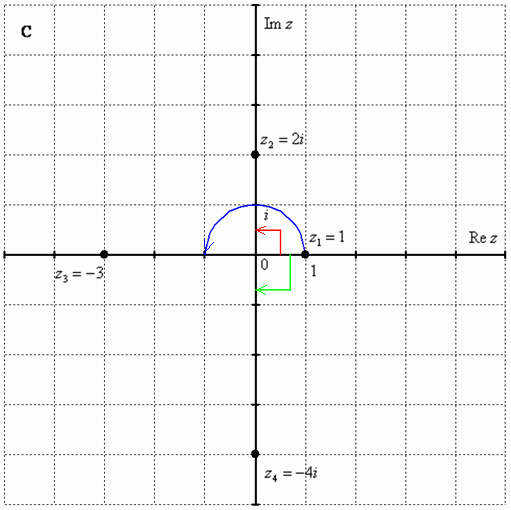
На самом деле задание устное. Для наглядности перепишу тригонометрическую форму комплексного числа: 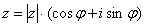
Запомним, модуль – длина (которая всегда неотрицательна), аргумент – угол.
1) Представим в тригонометрической форме число 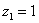 . Найдем его модуль и аргумент. Очевидно, что
. Найдем его модуль и аргумент. Очевидно, что 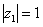 . Формальный расчет по формуле:
. Формальный расчет по формуле: 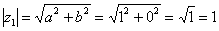 .
.
Очевидно, что 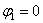 (число лежит непосредственно на действительной положительной полуоси). Таким образом, число в тригонометрической форме:
(число лежит непосредственно на действительной положительной полуоси). Таким образом, число в тригонометрической форме: 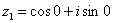 .
.
Ясно, обратное проверочное действие: 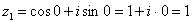
2) Представим в тригонометрической форме число 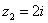 . Найдем его модуль и аргумент. Очевидно, что
. Найдем его модуль и аргумент. Очевидно, что 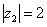 . Формальный расчет по формуле:
. Формальный расчет по формуле: 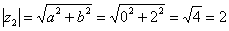 .
.
Очевидно, что 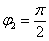 (или 90 градусов). На чертеже угол обозначен красным цветом. Таким образом, число в тригонометрической форме:
(или 90 градусов). На чертеже угол обозначен красным цветом. Таким образом, число в тригонометрической форме: 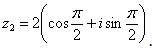
Используя таблицу значений тригонометрических функций, легко обратно получить алгебраическую форму числа (заодно выполнив проверку):
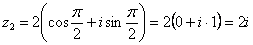
3) Представим в тригонометрической форме число 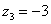 . Найдем его модуль и аргумент. Очевидно, что
. Найдем его модуль и аргумент. Очевидно, что 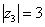 . Формальный расчет по формуле:
. Формальный расчет по формуле: 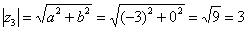 .
.
Очевидно, что 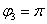 (или 180 градусов). На чертеже угол обозначен синим цветом. Таким образом, число в тригонометрической форме:
(или 180 градусов). На чертеже угол обозначен синим цветом. Таким образом, число в тригонометрической форме: 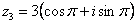 .
.
Проверка: 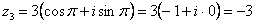
4) И четвёртый интересный случай. Представим в тригонометрической форме число 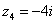 . Найдем его модуль и аргумент. Очевидно, что
. Найдем его модуль и аргумент. Очевидно, что 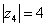 . Формальный расчет по формуле:
. Формальный расчет по формуле: 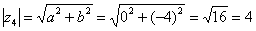 .
.
Аргумент можно записать двумя способами: Первый способ: 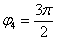 (270 градусов), и, соответственно:
(270 градусов), и, соответственно: 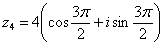 . Проверка:
. Проверка: 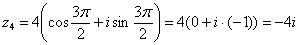
Однако более стандартно следующее правило: Если угол больше 180 градусов, то его записывают со знаком минус и противоположной ориентацией («прокруткой») угла: 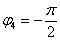 (минус 90 градусов), на чертеже угол отмечен зеленым цветом. Легко заметить, что
(минус 90 градусов), на чертеже угол отмечен зеленым цветом. Легко заметить, что 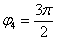 и
и 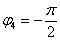 – это один и тот же угол.
– это один и тот же угол.
Таким образом, запись принимает вид: 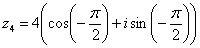
Внимание! Ни в коем случае нельзя использовать четность косинуса, нечетность синуса и проводить дальнейшее «упрощение» записи:
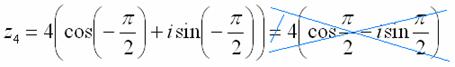
Пример 2.
Представить в тригонометрической форме комплексные числа: , 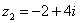 ,
, 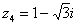 .
.
Представим в тригонометрической форме число 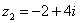 . Найдем его модуль и аргумент.
. Найдем его модуль и аргумент.
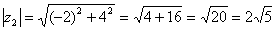
Поскольку 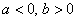 (случай 2), то
(случай 2), то 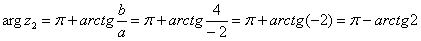 – вот здесь нечетностью арктангенса воспользоваться нужно. К сожалению, в таблице отсутствует значение
– вот здесь нечетностью арктангенса воспользоваться нужно. К сожалению, в таблице отсутствует значение 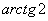 , поэтому в подобных случаях аргумент приходится оставлять в громоздком виде:
, поэтому в подобных случаях аргумент приходится оставлять в громоздком виде:
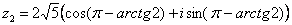 – число
– число 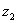 в тригонометрической форме
в тригонометрической форме
Представим в тригонометрической форме число 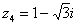 . Найдем его модуль и аргумент.
. Найдем его модуль и аргумент.
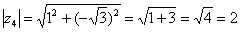
Поскольку 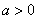 (случай 1), то
(случай 1), то 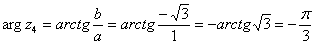 (минус 60 градусов).
(минус 60 градусов).
Таким образом:
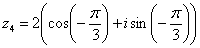 – число
– число 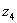 в тригонометрической форме.
в тригонометрической форме.
А вот здесь, как уже отмечалось, минусы не трогаем.
Используем таблицу значений тригонометрических функций, при этом учитываем, что угол 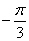 – это в точности табличный угол
– это в точности табличный угол 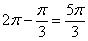 (или 300 градусов):
(или 300 градусов):
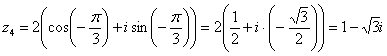 – число
– число 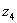 в исходной алгебраической форме.
в исходной алгебраической форме.
Любое комплексное число (кроме нуля) 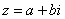 можно записать в показательной форме:
можно записать в показательной форме:
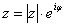 , где
, где 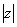 – это модуль комплексного числа, а
– это модуль комплексного числа, а 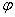 – аргумент комплексного числа.
– аргумент комплексного числа.
Что нужно сделать, чтобы представить комплексное число в показательной форме? Почти то же самое: выполнить чертеж, найти модуль и аргумент. И записать число в виде 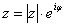 .
.
Например, для числа 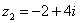 предыдущего примера у нас найден модуль и аргумент:
предыдущего примера у нас найден модуль и аргумент: 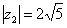 ,
, 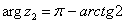 . Тогда данное число в показательной форме запишется следующим образом:
. Тогда данное число в показательной форме запишется следующим образом: 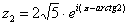 .
.
Число 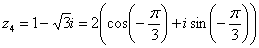 в показательной форме будет выглядеть так:
в показательной форме будет выглядеть так: 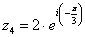
Число 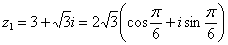 – так:
– так: 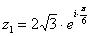
И т.д.
Единственный совет – не трогаем показатель экспоненты, там не нужно переставлять множители, раскрывать скобки и т.п. Комплексное число в показательной форме записывается строго по форме 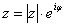 .
.
Пример 3.
Дано комплексное число 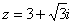 , найти
, найти 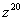 .
.
Что нужно сделать? Сначала нужно представить данной число в тригонометрической форме.
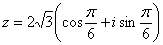
Тогда, по формуле Муавра:
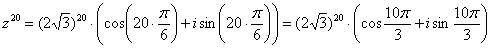
Не нужно считать на калькуляторе 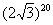 , а вот угол в большинстве случае следует упростить. Как упростить? Образно говоря, нужно избавиться от лишних оборотов. Один оборот составляет
, а вот угол в большинстве случае следует упростить. Как упростить? Образно говоря, нужно избавиться от лишних оборотов. Один оборот составляет 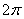 радиан или 360 градусов. Выясним сколько у нас оборотов в аргументе
радиан или 360 градусов. Выясним сколько у нас оборотов в аргументе 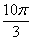 . Для удобства делаем дробь правильной:
. Для удобства делаем дробь правильной: 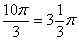 , после чего становится хорошо видно, что можно убавить один оборот:
, после чего становится хорошо видно, что можно убавить один оборот: 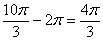 . Понятно, что
. Понятно, что 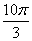 и
и 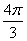 – это один и тот же угол.
– это один и тот же угол.
Таким образом, окончательный ответ запишется так:
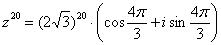 .
.
Можно переписать ответ в виде:
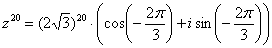 (т.е. убавить еще один оборот и получить значение аргумента в стандартном виде).
(т.е. убавить еще один оборот и получить значение аргумента в стандартном виде).
Хотя 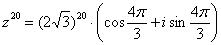 – ни в коем случае не ошибка.
– ни в коем случае не ошибка.
Пример 4.
Дано комплексное число 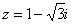 , найти
, найти 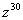 . Полученный аргумент (угол) упростить, результат представить в алгебраической форме.
. Полученный аргумент (угол) упростить, результат представить в алгебраической форме.
Отдельная разновидность задачи возведения в степень – это возведение в степень чисто мнимых чисел.
Пример 5.
Возвести в степень комплексные числа 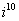 ,
, 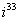 ,
, 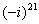
Здесь тоже всё просто, главное, помнить знаменитое равенство.
Если мнимая единица возводится в четную степень, то техника решения такова:
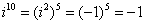
Если мнимая единица возводится в нечетную степень, то «отщипываем» одно «и», получая четную степень:
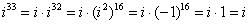
Если есть минус (или любой действительный коэффициент), то его необходимо предварительно отделить:
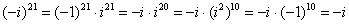
Извлечение корней из комплексных чисел.
Квадратное уравнение с комплексными корнями.
Пример 6.
Решить квадратное уравнение 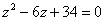
Вычислим дискриминант:
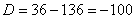
Дискриминант отрицателен, и в действительных числах уравнение решения не имеет. Но корень можно извлечь в комплексных числах!
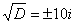
По известным школьным формулам получаем два корня:
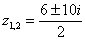
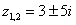 – сопряженные комплексные корни
– сопряженные комплексные корни
Таким образом, уравнение 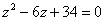 имеет два сопряженных комплексных корня:
имеет два сопряженных комплексных корня: 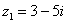 ,
, 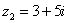
Теперь вы сможете решить любое квадратное уравнение!
И вообще, любое уравнение с многочленом «энной» степени 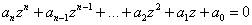 имеет ровно
имеет ровно 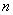 корней, часть из которых может быть комплексными.
корней, часть из которых может быть комплексными.
Простой пример для самостоятельного решения:
Пример 7.
Найти корни уравнения 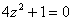 и разложить квадратный двучлен на множители.
и разложить квадратный двучлен на множители.
Разложение на множители осуществляется опять же по стандартной школьной формуле.
Как извлечь корень из произвольного комплексного числа?
Рассмотрим уравнение 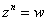 , или, то же самое:
, или, то же самое: 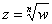 . Здесь «эн» может принимать любое натуральное значение, которое больше единицы. В частности, при
. Здесь «эн» может принимать любое натуральное значение, которое больше единицы. В частности, при 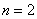 получается квадратный корень
получается квадратный корень 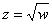
Уравнение вида 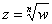 имеет ровно
имеет ровно 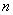 корней
корней 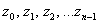 , которые можно найти по формуле:
, которые можно найти по формуле:
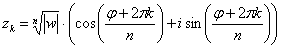 , где
, где 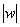 – это модуль комплексного числа
– это модуль комплексного числа 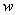 ,
, 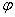 – его аргумент, а параметр
– его аргумент, а параметр 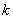 принимает значения:
принимает значения: 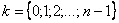
Пример 8.
Найти корни уравнения 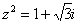
Перепишем уравнение в виде 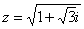
В данном примере 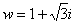 ,
, 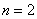 , поэтому уравнение будет иметь два корня:
, поэтому уравнение будет иметь два корня: 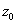 и
и 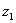 .
.
Общую формулу можно сразу немножко детализировать:
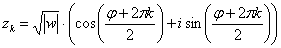 ,
, 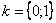
Теперь нужно найти модуль и аргумент комплексного числа 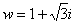 :
:
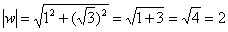
Число 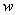 располагается в первой четверти, поэтому:
располагается в первой четверти, поэтому:
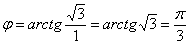
Напоминаю, что при нахождении тригонометрической формы комплексного числа всегда желательно сделать чертеж.
Еще более детализируем формулу:
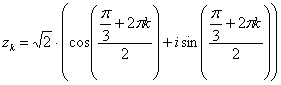 ,
, 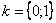
На чистовик так подробно оформлять, конечно, не нужно, это сделано мной для того, чтобы вам было понятно, откуда что взялось.
Подставляя в формулу значение 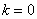 , получаем первый корень:
, получаем первый корень:
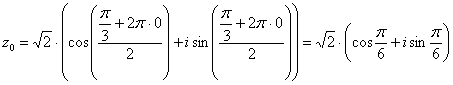
Подставляя в формулу значение 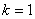 , получаем второй корень:
, получаем второй корень:
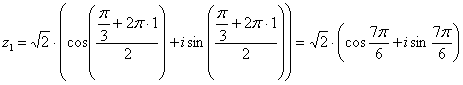
Ответ: 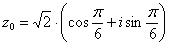 ,
, 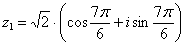
При желании или требовании задания, полученные корни можно перевести обратно в алгебраическую форму.
Пример 9: Решение:
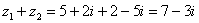
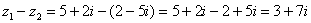
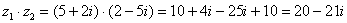
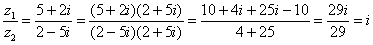
Пример 10: Решение:
Представим в тригонометрической форме число 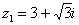 . Найдем его модуль и аргумент.
. Найдем его модуль и аргумент. 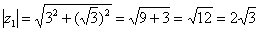 . Поскольку
. Поскольку 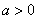 (случай 1), то
(случай 1), то 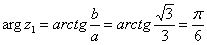 . Таким образом:
. Таким образом: 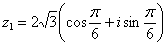 – число
– число 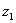 в тригонометрической форме.
в тригонометрической форме.
Представим в тригонометрической форме число 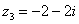 . Найдем его модуль и аргумент.
. Найдем его модуль и аргумент. 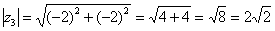 . Поскольку
. Поскольку 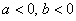 (случай 3), то
(случай 3), то 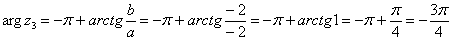 . Таким образом:
. Таким образом: 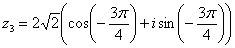 – число
– число 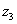 в тригонометрической форме.
в тригонометрической форме.
Пример 11: Решение: Представим число в тригонометрической форме: 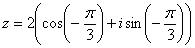 . Используем формулу Муавра
. Используем формулу Муавра 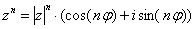 :
:

Пример 12: Решение:
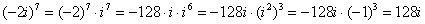
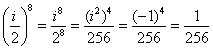
Пример 13: Решение:
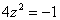
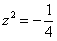
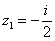 ,
, 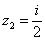
Разложим квадратный двучлен на множители: