Ассмотрим линейную регрессию.
Составим исходную расчетную таблицу. Для удобства можно добавить в нее еще два столбца: 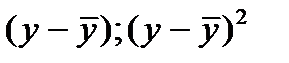 , чтобы сразу получить общую сумму квадратов.
, чтобы сразу получить общую сумму квадратов.
| № п/п | Объем товарооборота 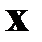 (тыс. руб.) (тыс. руб.) | Издержки 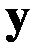 (тыс. руб.) (тыс. руб.) | 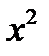 | 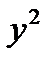 | 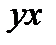 | 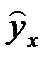 | 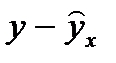 | 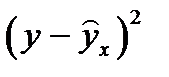 | 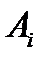 |
| 12,6 | 158,76 | 12,2 | +0,4 | 0,16 | 3,17 | ||||
| 6,7 | 44,89 | 7,2 | -0,5 | 0,25 | 7,46 | ||||
| 11,2 | 125,44 | 10,9 | +0,3 | 0,09 | 2,68 | ||||
| 9,6 | 92,16 | 9,6 | |||||||
| 3,4 | 11,56 | 3,3 | 0,1 | 0,01 | 2,94 | ||||
| 8,4 | 70,56 | 8,4 | |||||||
| 2,8 | 7,84 | 2,7 | 0,1 | 0,01 | 3,57 | ||||
| 13,0 | 13,4 | -0,4 | 0,16 | 3,08 | |||||
| 6,1 | 37,21 | 5,9 | 0,2 | 0,04 | 3,28 | ||||
| 1,9 | 3,61 | 2,1 | -0,2 | 0,04 | 10,53 | ||||
| Итого | 75,7 | 721,03 | 75,7 | 0,76 | 36,71 | ||||
| Сред.зн. | 103,5 | 7,57 | 11632,5 | 72,1 | 899,9 | 7,57 | - | - | 3,671 |
Функция издержек выразится зависимостью: 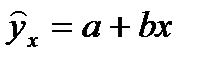 .
.
 Для определения коэффициентов «a» и «b» воспользуемся методом наименьших квадратов (МНК):
Для определения коэффициентов «a» и «b» воспользуемся методом наименьших квадратов (МНК):
(1) 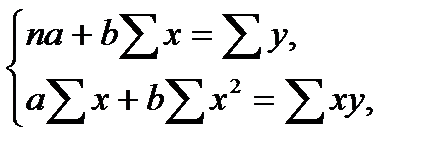

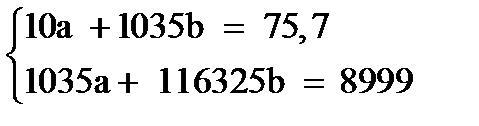
Домножим уравнение (1) системы на (-103,5), получим систему, которую решим методом алгебраического сложения.
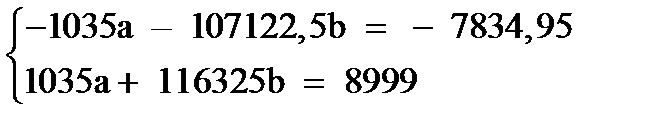
9202,5b = 1164,05  или b = 0,12649.
или b = 0,12649.
Коэффициент корреляции b можно находить по формуле (2), не решая систему (1) непосредственно:
(2) 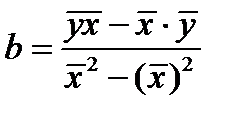 ,
, 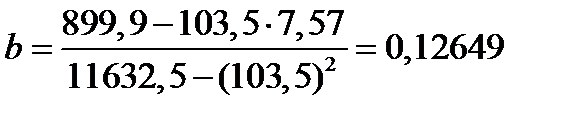
Результат аналогичен.
Теперь найдем коэффициент «a» из уравнения (1) системы (1):
10a = 75,7-1035b; 10a = 75,71035*0,12649; 10a =- 55,2;
a = -5,52.
Или можно «a» вычислить по формуле (3) 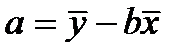 ,
,
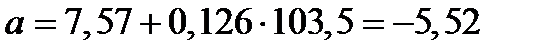 .
.
Уравнение регрессии будет иметь вид: 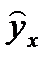 = -5,52 + 0,126 x
= -5,52 + 0,126 x
Затем, подставляя различные значения 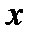 из столбца 2, получим теоретические значения
из столбца 2, получим теоретические значения 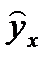 для столбца 7:
для столбца 7:
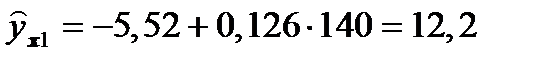 ,
,
аналогично для 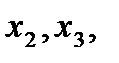 …и
…и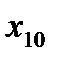 .
.
В столбце 8 находим разность текущего значения 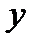 и
и 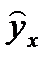 (теоретического), найденного по формуле (4).
(теоретического), найденного по формуле (4).
Для расчета используем следующие формулы:
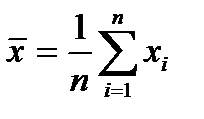 ,
, 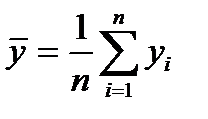 ,
, 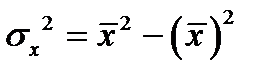 ,
,
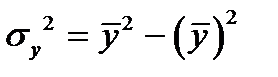 ,
, 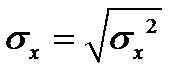 ,
, 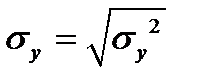 .
.
Коэффициент аппроксимации определим по формуле:
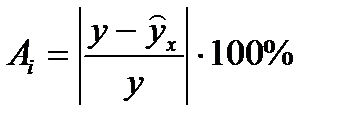 .
.
Средняя ошибка аппроксимации:
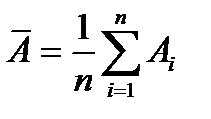 .
.
Допустимый предел значений 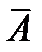 - не более 10 %, это говорит о том, что уравнение регрессии точно аппроксимирует исходную зависимость.
- не более 10 %, это говорит о том, что уравнение регрессии точно аппроксимирует исходную зависимость.
Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции 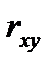 . Найдем его по формуле для
. Найдем его по формуле для 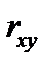
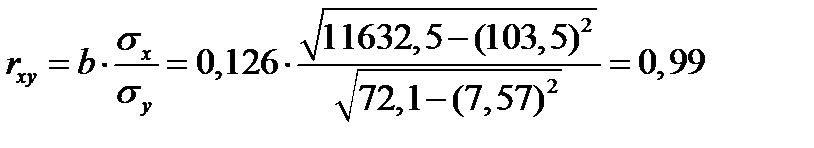 .
.
Коэффициент 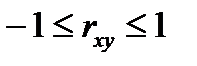 . Характер связи устанавливается по таблице Чеддока:
. Характер связи устанавливается по таблице Чеддока:
| Диапазон измерения | 0,1-0,3 | 0,3-0,5 | 0,5-0,7 | 0,7-0,9 | 0,9-0,99 |
| Характер тесноты связи | слабая | умеренная | заметная | высокая | весьма высокая |
В примере получилась связь прямая, весьма высокая.
Для вычисления коэффициента 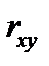 , используются и другие формулы:
, используются и другие формулы:
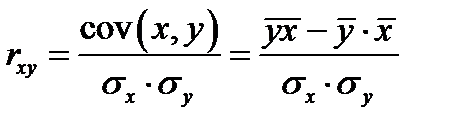 .
.
3. Дисперсионный анализ. Общая сумма квадратов отклонений (т.е. общая дисперсия ) равна:
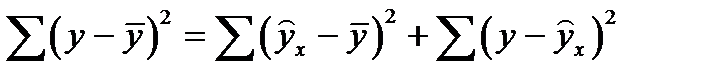 ,
,
где 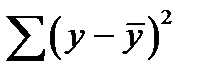 - общая сумма квадратов отклонений,
- общая сумма квадратов отклонений,
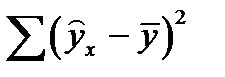 - сумма отклонений, обусловленная регрессией (факторная),
- сумма отклонений, обусловленная регрессией (факторная),
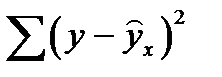 - остаточная сумма квадратов отклонений.
- остаточная сумма квадратов отклонений.
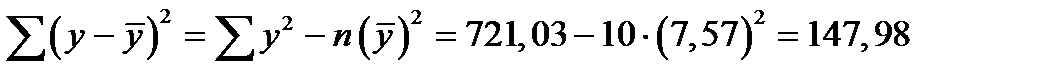 .
.
Остаточная сумма 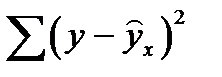 определена в таблице в 9 столбце и равна 0,76. Тогда объясненная (факторная) сумма квадратов будет равна
определена в таблице в 9 столбце и равна 0,76. Тогда объясненная (факторная) сумма квадратов будет равна 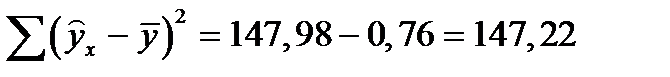
Долю дисперсии, объясняемую регрессией, в общей доле дисперсии 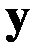 характеризует индекс детерминации
характеризует индекс детерминации 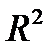 . Он определяется отношением объясненной дисперсии к общей
. Он определяется отношением объясненной дисперсии к общей 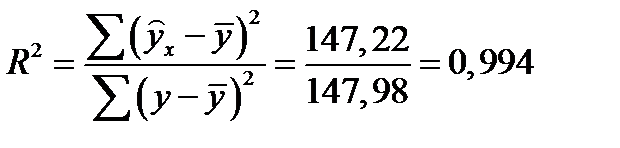 .
.
Качество всего уравнения регрессии в целом, проверяется F-тестом.
Составим таблицу дисперсионного анализа:
| Источники вариации | Число степеней свободы | 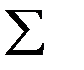 квадр. отклонений. квадр. отклонений. | Дисперсия на 1 степ. свободы. | F отн | |
| Факт | табл. (0,05) | ||||
| общая | 147,98 | 147,22 | 1549,68 | 5,32 | |
| объясненная | 147,22 | ||||
| остаточная | 0,76 | 0,095 |
Fтабл определяем по [1] в зависимости от уровня значимости (α = 0,05) и числа степеней свободы (df=8). Fтабл=5,32.
F-тест состоит в проверке гипотезы Но о статистической незначимости уравнения регрессии и показателя тесноты связи rху.
Если Fфакт >Fтабл (1549>5,32), то гипотеза Но о случайной природе оцениваемых характеристик отклоняется и признается их значимость и надежность.
Б) Степенная регрессия 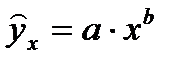
Для того, чтобы построить степенную модель, необходимо линеаризовать переменные путем логарифмирования обеих частей уравнения 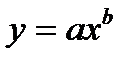 :
:
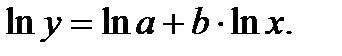
Пусть 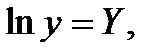
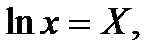
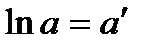 , тогда
, тогда 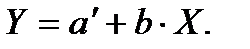
Рассчитываем 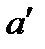 и b по формулам:
и b по формулам:
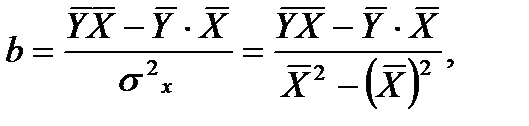
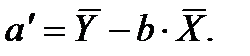
Все необходимые расчеты представлены в таблице 2.
| № п/п | x | y | X | Y | XY | X2 | Y2 | 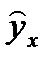 | 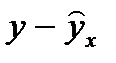 | 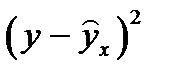 | Ai |
| 12,6 | 4,9416 | 2,5337 | 12,2053 | 24,4198 | 6,4196 | 11,6 | 1,0 | 1,0 | 7,9 | ||
| 6,7 | 4,6052 | 1,9021 | 8,7596 | 21,2076 | 3,6180 | 6,7 | |||||
| 11,2 | 4,8675 | 2,4159 | 11,7594 | 23,6929 | 5,8366 | 10,7 | 0,5 | 0,25 | 3.73 | ||
| 9,6 | 4,7875 | 2,2617 | 10,8282 | 22,9201 | 5,1156 | 9,3 | 0,3 | 0,09 | 0,93 | ||
| 3,4 | 4,2485 | 1,2237 | 5,1702 | 18,0497 | 1,4976 | 3,7 | 0,3 | 0,09 | 2,64 | ||
| 8,4 | 4,7005 | 2,1282 | 10,0037 | 22,0945 | 4,5294 | 7,8 | 0,6 | 0,36 | 4,28 | ||
| 2,8 | 4,1744 | 1,0296 | 4,2980 | 17,4255 | 1,0601 | 3,4 | - 0,6 | 0,36 | 12,8 | ||
| 13,0 | 5,0106 | 2,5649 | 12,8519 | 25,1065 | 6,5790 | 12,9 | 0,1 | 0,01 | 0,08 | ||
| 6,1 | 4,4998 | 1,8083 | 8,1369 | 20,2483 | 3,2699 | 5,7 | 0,4 | 0,16 | 2,62 | ||
| 1,9 | 4,0943 | 0,6418 | 2,6279 | 16,7637 | 0,4120 | 2,9 | - 1,0 | 1,0 | 52,6 | ||
| Итого | 75,7 | 45,9299 | 18,5099 | 86,6419 | 211,9286 | 37,9258 | 74,7 | 1,6 | 3,32 | 87,59 | |
| Средн.зн. | 103,5 | 7,57 | 4,59299 | 1,85099 | 8,66419 | 21,19286 | 3,79258 | 8,759 |
Параметры будут равны: 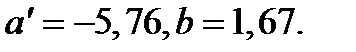
Подставим их в уравнение и получим линейное уравнение:
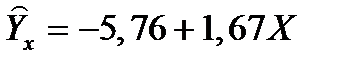
Потенцируя которое, получим:
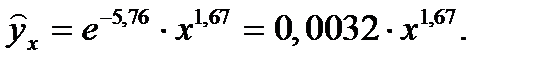
По этому уравнению заполняется вторая половина таблицы.
В) Уравнение гиперболы 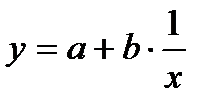
Линеаризуется при замене 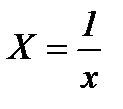 , тогда
, тогда 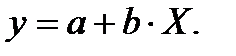
Все необходимые расчеты представим в таблице 6.
| № п/п | x | y | 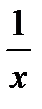 | 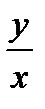 | 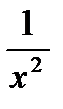 | 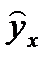 | 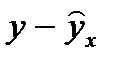 | 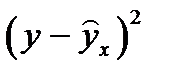 | Ai |
| 12,6 | 0,0071429 | 0,05 | 0,000051 | 10,7 | 1,9 | 3,61 | |||
| 6,7 | 0,01 | 0,067 | 0,0001 | 8,1 | -1,4 | 1,96 | |||
| 11,2 | 0,007692 | 0,086154 | 0,000059 | 10,3 | 0,9 | 0,81 | |||
| 9,6 | 0,008333 | 0,08 | 0,000069 | 9,6 | |||||
| 3,4 | 0,014286 | 0,048571 | 0,000204 | 4,2 | -0,8 | 0,64 | |||
| 8,4 | 0,009091 | 0,076364 | 0,000083 | 8,9 | -0,5 | 0,25 | 5,9 | ||
| 2,8 | 0,015385 | 0,043077 | 0,000237 | 3,2 | -0,4 | 0,16 | |||
| 13,0 | 0,006667 | 0,086667 | 0,000044 | 11,3 | 1,7 | 2,89 | |||
| 6,1 | 0,011111 | 0,067778 | 0,000125 | 7,1 | -1 | ||||
| 1,9 | 0,016667 | 0,031667 | 0,000278 | -0,1 | 0,01 | 5,2 | |||
| Сумма | 75,7 | 0,106375 | 0,434124 | 0,001537 | 75,5 | 11,33 | 120,1 | ||
| Ср. знач. | 103,5 | 7,57 | 0,0106375 | 0,0434124 | 0,000154 |
Найдем параметры 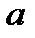 и
и 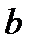 , используя МНК.
, используя МНК.
Для этого решим систему (1), учитывая, что 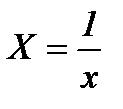 .
.
Таким образом, получили систему уравнений:
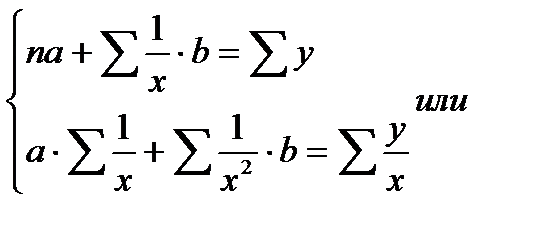 :
: 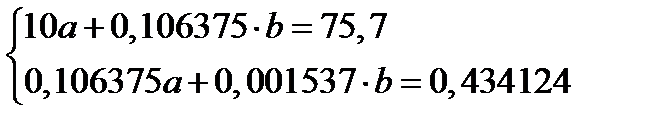 :
:
Можно воспользоваться формулами.
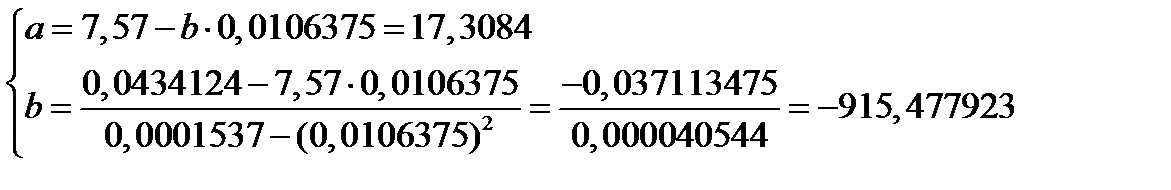
Итак, получим уравнение:
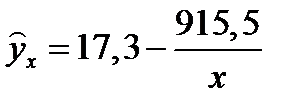 .
.
Оценим тесноту связи результативным фактором и факторным признаком с помощью индекса корреляции 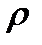 (для нелинейных моделей) и коэффициента детерминации
(для нелинейных моделей) и коэффициента детерминации 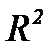 , которые рассчитываются по следующим формулам:
, которые рассчитываются по следующим формулам:
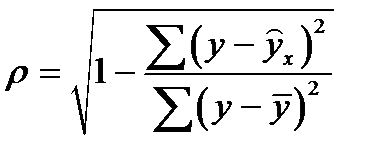 ,
,
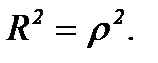
Для степенной регрессии: 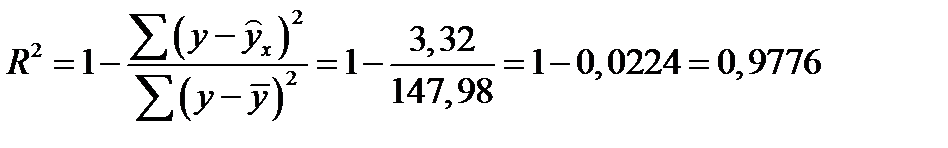
Для гиперболы получим: ……………………………………… 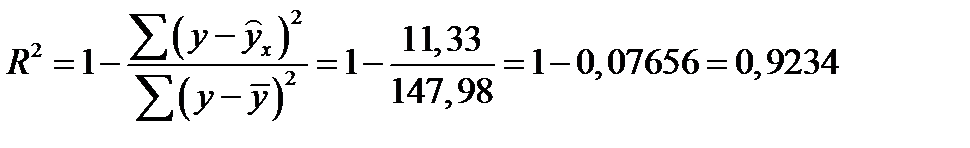
Найдем средний коэффициент эластичности по формулам, представленным в таблице 7.
Таблица 7
| Вид регрессии | Формула для расчета |
| Линейная | 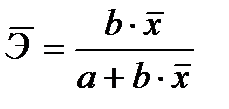 |
| Степенная | 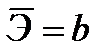 |
| Гиперболическая | 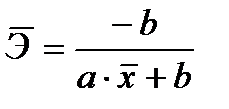 |
Найдем среднюю ошибку аппроксимации по формуле:
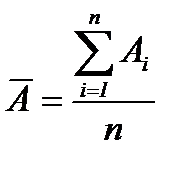 , где
, где 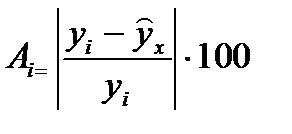 .
.
Оценим статистическую надежность результатов регрессионного моделирования с помощью F-критерия Фишера:
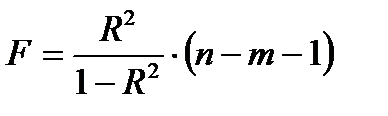 .
.
Для степенной регрессии имеем:
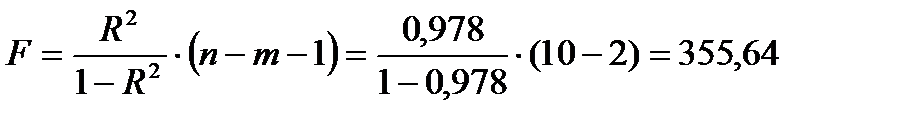 .
.
Для гиперболы
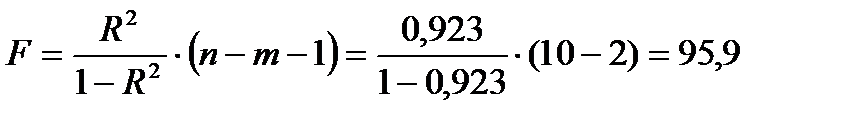 .
.
Для линейном модели уже строили таблицу дисперсионного анализа
Для сравнения полученных уравнений регрессии построим следующую таблицу:
Таблица
| Вид регрессии | 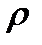 , ,  | R2, r2 | 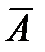 | 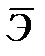 | F | 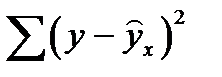 |
| Линейная | 0,997 | 0,994 | 3,67 | 1,3973 | 0,76 | |
| Степенная | 0,988 | 0,978 | 8,76 | 1,2558 | 355,64 | 3,32 |
| Гиперболическая | 0,961 | 0,923 | 1,0796 | 95,90 | 11,33 |
Из итоговой таблицы видно, что коэффициент корреляции наибольший для линейной регрессии, коэффициент детерминации max, а коэффициент аппроксимации минимален, поэтому можно сделать вывод: наиболее сильное влияние на уровень издержек в зависимости от товарооборота получается при использовании в качестве аппроксимирующей функции линейную функцию.
Для всех моделей 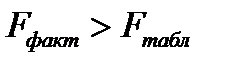 , следовательно, все модели являются адекватными.
, следовательно, все модели являются адекватными.
Из таблицы видно, что лучшим уравнением регрессии является линейная функция, так как коэффициент детерминации для этой функции является наибольшим из представленных в таблице, сумма квадратов отклонений фактических значений результативного признака от расчетных является наименьшей и средний коэффициент аппроксимации является наименьшим.
Если получается, что коэффициент детерминации для нелинейной регрессии 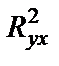 больше
больше 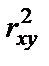 коэффициента детерминации для линейной регрессии, надо рассмотреть модуль
коэффициента детерминации для линейной регрессии, надо рассмотреть модуль 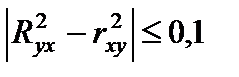 . Если разность небольшая, т.е. условие модуля выполняется, то все равно выбираем линейную регрессию для дальнейших расчетов.
. Если разность небольшая, т.е. условие модуля выполняется, то все равно выбираем линейную регрессию для дальнейших расчетов.
Чем больше кривизна линии регрессии, тем 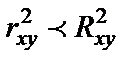 <
< 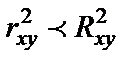 . Если
. Если 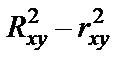 превышает 0,1, то предположение о линейной форме связи считается не оправданным. В этом случае проводится оценка существенности различия
превышает 0,1, то предположение о линейной форме связи считается не оправданным. В этом случае проводится оценка существенности различия 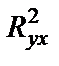 по критерию Стьюдента.
по критерию Стьюдента. 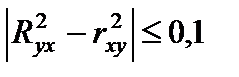
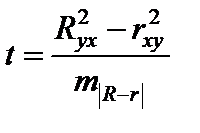
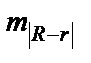 - ошибка разности между
- ошибка разности между 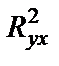 и
и 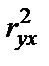
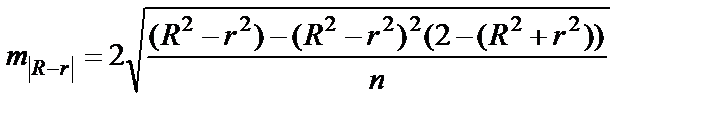
Если t < 2, то различия между 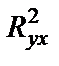 и
и 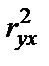 несущественны, и возможно применение линейной регрессии.
несущественны, и возможно применение линейной регрессии.
Если t >2, то различия существенны и замена нелинейной регрессии уравнением линейной функции невозможна.
В нашем примере лучшей является линейная модель. Для линейной регрессии выполним дальнейшие расчеты.
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитывают t-критерий.
Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:
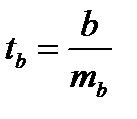 ,
, 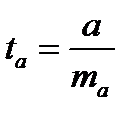 ,
, 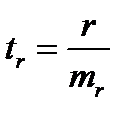 .
.
;
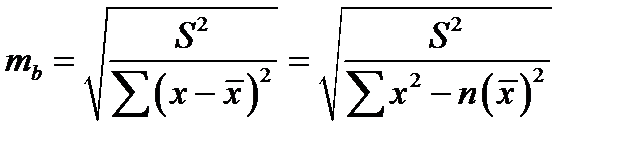 ,
,
где 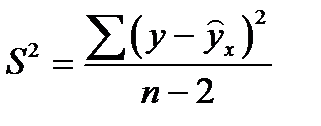 , или из табл. дисперсионного анализа (0,095).
, или из табл. дисперсионного анализа (0,095).
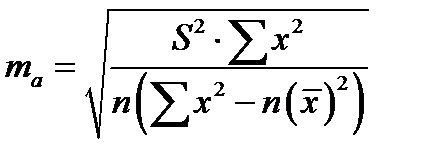 ,
, 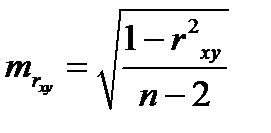 .
.
Для примера определим стандартную ошибку для параметра «b»:
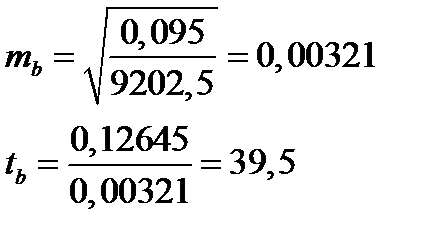
Критерий Стьюдента для параметра «b» равен 39,5.
Связь между F-критерием Фишера и t-статистикой Стьюдента выражается равенством:

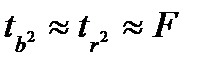 , 39,52=1560.
, 39,52=1560.
Табличное значение tтабл критерия Стьюдента определяем по [1] для и уровня значимости 0,05 и числа степеней свободы df = 8, 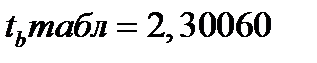 , т.к.
, т.к. 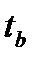 >
> 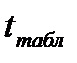 , то гипотезу о несущественности коэффициента регрессии можно отклонить.
, то гипотезу о несущественности коэффициента регрессии можно отклонить.
Для расчета доверительного интервала определяем предельную ошибку  для каждого показателя:
для каждого показателя:
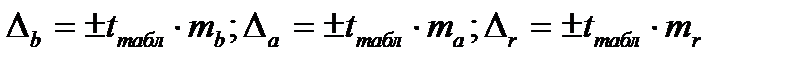
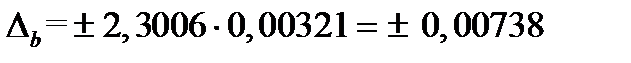
Доверительный интервал, 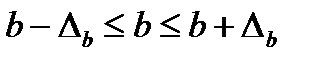 ,
, 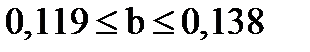 .
.
Для расчета доверительного интервала для параметра а, найдем:
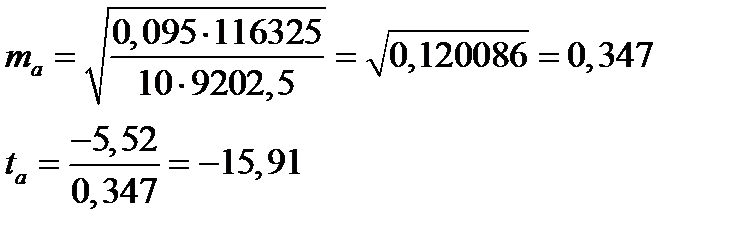
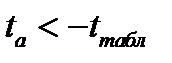 , т.к. критерий Стьюдента двусторонний, а параметр а - отрицательный, то он значим. Найдем для него доверительный интервал:
, т.к. критерий Стьюдента двусторонний, а параметр а - отрицательный, то он значим. Найдем для него доверительный интервал:
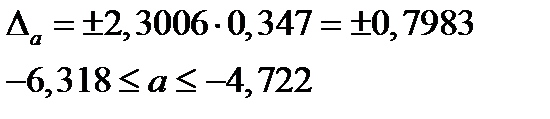
Найдем доверительный интервал для параметра r:
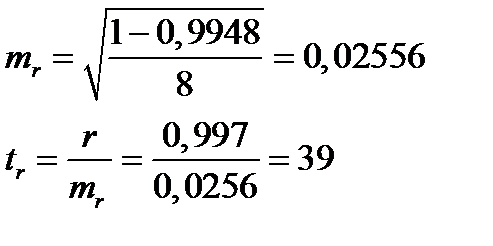
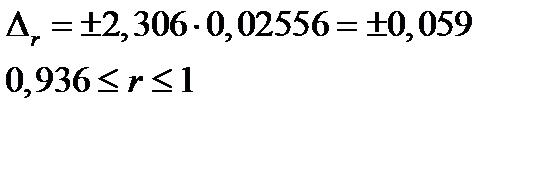
Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательная, а верхняя положительная, то оцениваемый параметр принимается нулевым, т.к. не может одновременно принимать и положительное и отрицательное значения.
Прогнозное значение 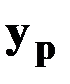 определяется путем подстановки в уравнение регрессии:
определяется путем подстановки в уравнение регрессии:
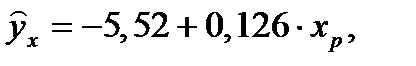
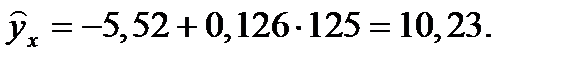
Вычислим ошибку прогноза для уравнения 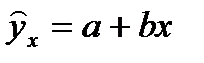 :
:
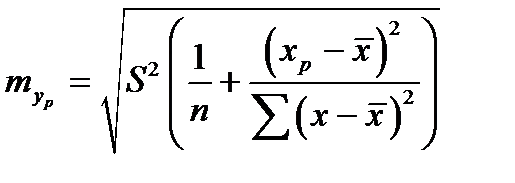 .
.
И для уравнения 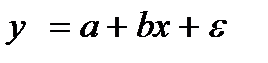 :
:
(*) 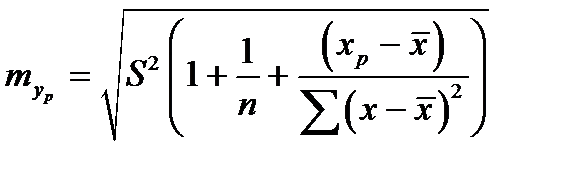 ,
,
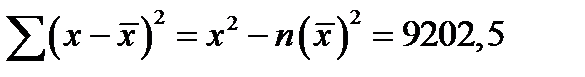 ,
,
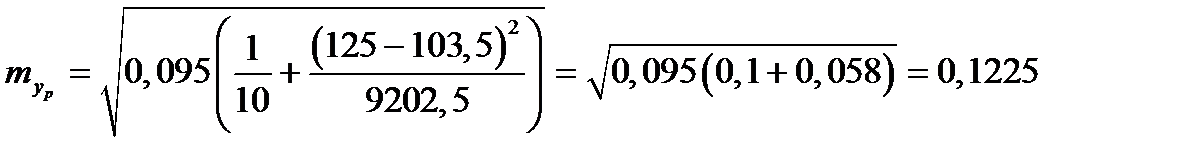 .
.
Для * 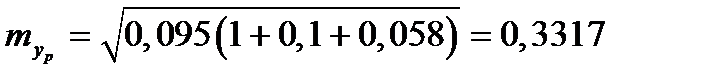 ,
,
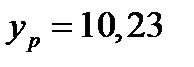 ,
,
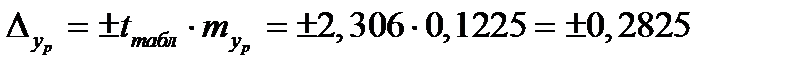 ,
,
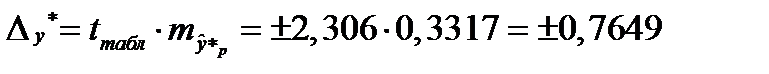 ,
,
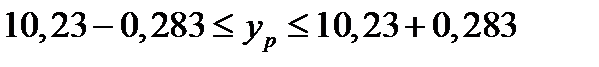 ,
,
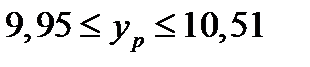 .
.
Для уравнения с 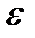 :
:
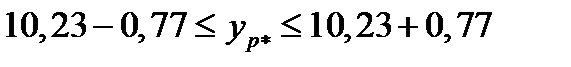 ,
,
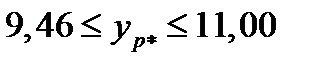 .
.
Библиографический список рекомендуемой литературы
1. Кремер Н.Ш. Эконометрика [Электронный ресурс]: учебник / Кремер Н.Ш., Путко Б.А. —Электрон. текстовые данные. — М.: ЮНИТИ-ДАНА, 2012, — 328 с.— Режим доступа: http// www. iprbookshop.ru /8594. — ЭБС «IPRbooks», по паролю
2. Елисеева, И.И. Эконометрика: учебник для вузов /И.И. Елисеева [и др.]; под ред. И.И. Елисеевой.— М.: Проспект, 2013 .— 288с.
3. Елисеева И.И. Практикум по эконометрике: учебное пособие для экономических вузов./И.И. Елисеева [и др.]; под ред. И.И. Елисеевой .— 2-е изд., перераб. и доп. — М. : Финансы и статистика, 2008 .— 344с.+1 опт. диск (CD-ROM).
4. Эконометрика [Электронный ресурс]: учебно-мультимедийный компьютерный курс .— Multimedia (110MB) .— М. : Диполь, 2007 .— 1 опт. диск. (CD ROM) .— (Вузовская серия).
5. Новиков А.И. Эконометрика: Учеб.пособие. - М.: ИНФРА-М, 2010. - 144 с.
Периодические издания
1. Журнал «Проблемы прогнозирования» c 2011 по 2013 гг.
2. Журнал «Экономика и математические методы» c 2011 по 2013 гг.
3. Прикладная эконометрика [Электронный ресурс]: Научно-практический журнал.— Режим доступа: http// www.elibrari.ru/ projeets/subscripfion/rus titles open.nsp.
Интернет-ресурсы
1. Электронный читальный зал "БИБЛИОТЕХ" : учебники авторов ТулГУ по всем дисциплинам. - Режим доступа: https://tsutula.bibliotech.ru/, по паролю.- Загл. с экрана
2. ЭБС IPRBooks универсальная базовая коллекция изданий. - Режим доступа: http://www.iprbookshop.ru/, по паролю.
3. Научная Электронная Библиотека eLibrary - библиотека электронной периодики.- Режим доступа: http://elibrary.ru/ , по паролю.- Загл. с экрана.
4. НЭБ КиберЛенинка научная электронная библиотека открытого доступа, режим доступа http://cyberleninka.ru/ ,свободный.- Загл. с экрана.
5. Единое окно доступа к образовательным ресурсам: портал [Электронный ресурс]. - Режим доступа : http: //window.edu.ru. - Загл. с экрана.
6. www.gks.ru / Федеральная служба государственной статистики/
7. www.minfin.ru / Министерство финансов РФ
8. www.minpromtorg.gov.ru / Министерство промышленности и торговли РФ/
