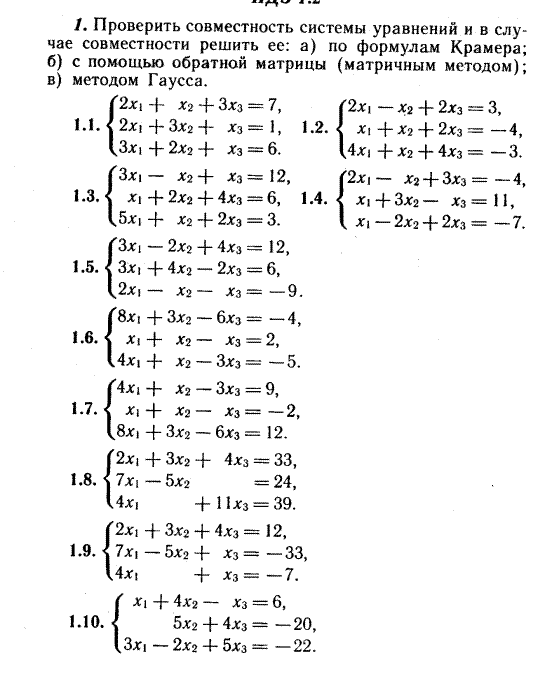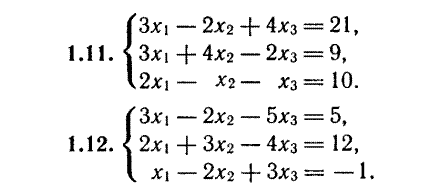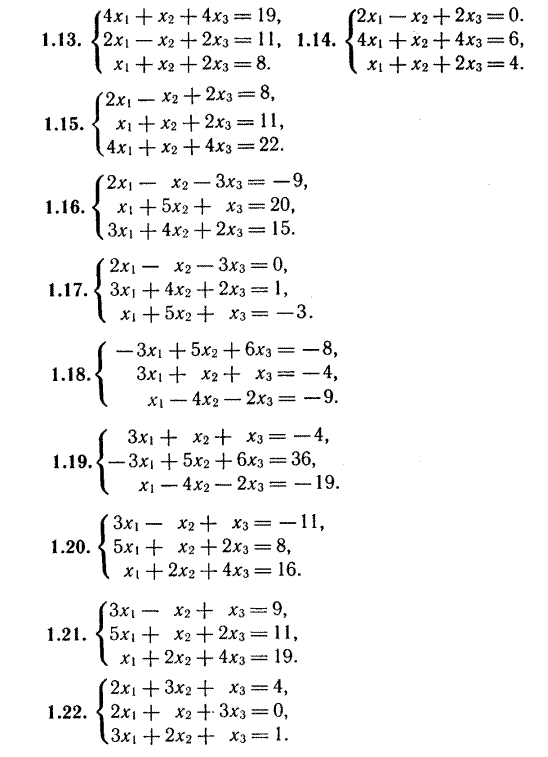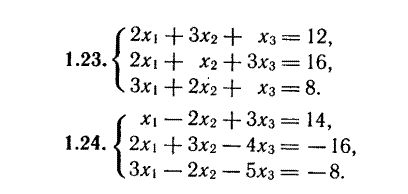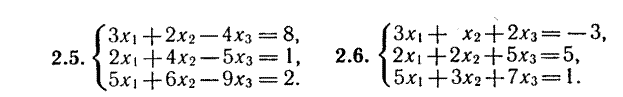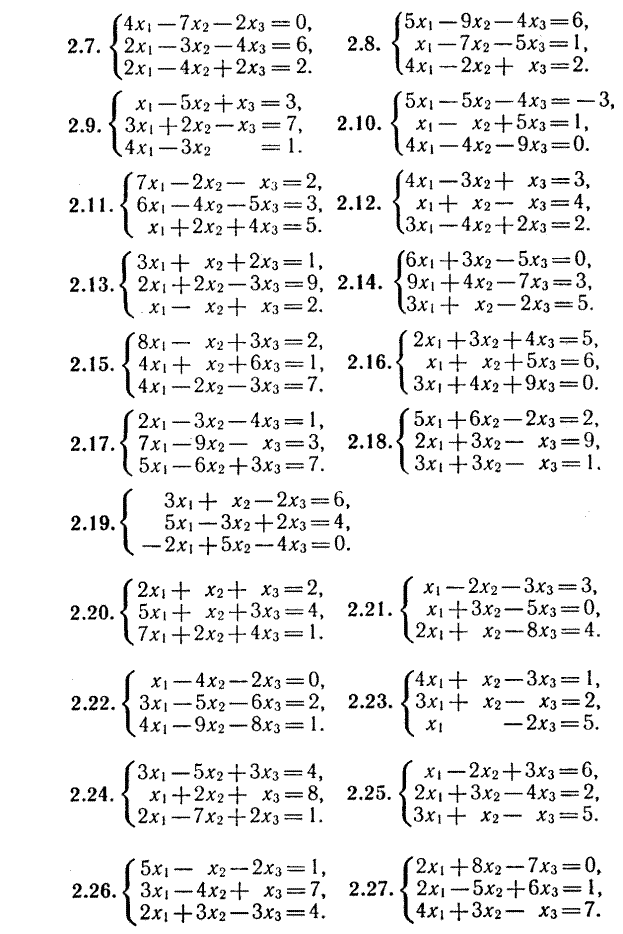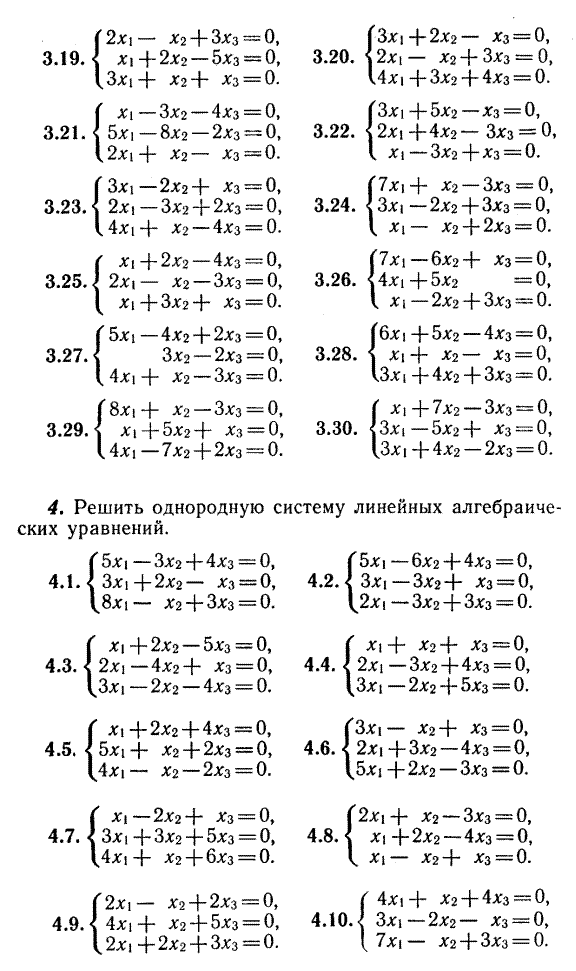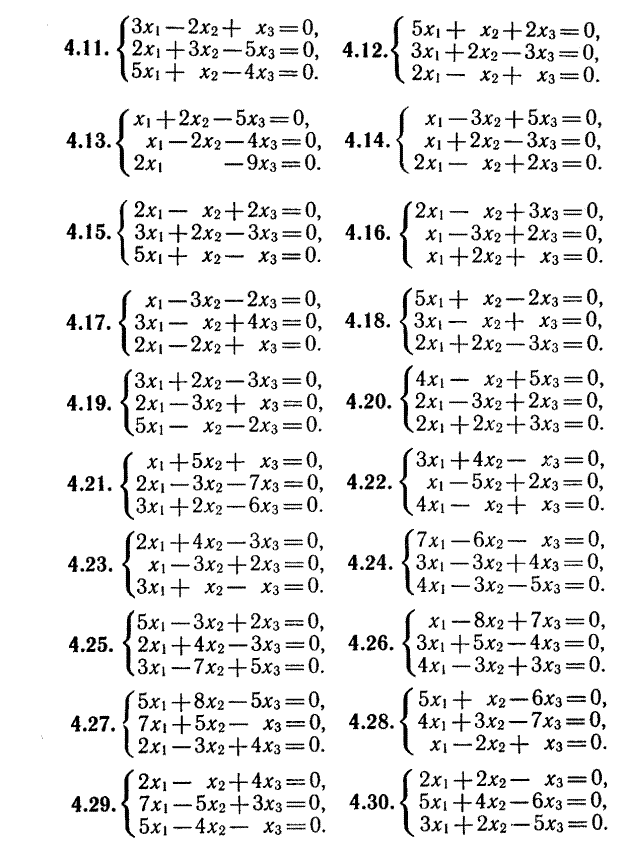Системы линейных уравнений.
Збірник завдань
для аудиторної та самостійної роботи
з дисципліни « Вища математика»
за темою « Елемети лінійної алгебри»
для спеціальності 5.0501201 «Обслуговування комп’ютерних систем і мереж”,
5.05090306 «Монтаж, технічне обслуговування і ремонт обладнання радіозв’язку, радіомовлення та телебачення.”
Завдання для самостійної та індивідуальної роботи
Розробила Мілютіна О.С., викладач вищої категорії, ст.. викладач
Задания с решениями
- Вычислить определитель третьего порядка

Решение Разложив определитель по элементам 1-й строки, получим
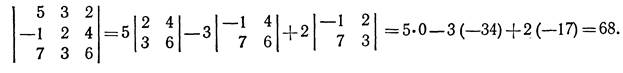
- Вычислить тот же определитель на основании теоремы о линейной комбинации элементов строк (столбцов).
Решение К элементам 1-й строки прибавим соответствующие элементы 2-й строки,
умноженные на 5, а к элементам 3-й строки—соответствующие элементы 2-й строки, умноженные на 7:
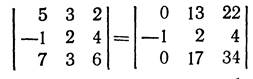
Разложив определитель по элементам 1-го столбца, получаем
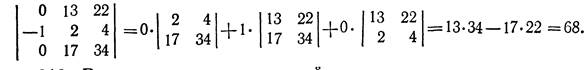
.
Задачи
1.Вычислить определитель
а)  б)
б) 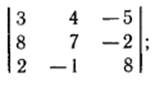 в)
в) 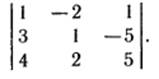
г) 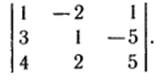 д)
д) 
2. Вычислить определитель
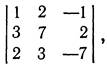
разложив его по элементам 3-й строки.
3. Вычислить определитель


МАТРИЦЫ
Задачи с решениями
1. Найти сумму матриц
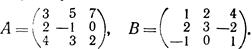
Решение
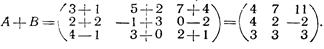
2 Найти матрицу 2А + 5В, если
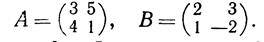
Решение
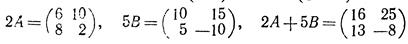
- Найти произведения матриц АВ и В А, если
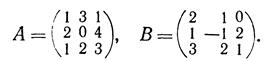
Решение
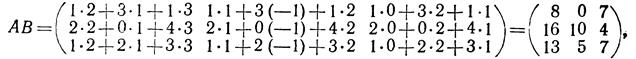
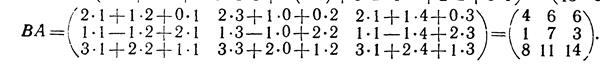 4. Найти А3, если
4. Найти А3, если
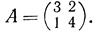
Решение
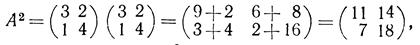
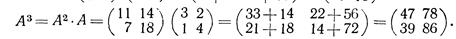
5. Найти значение матричного многочлена 2А2 + ЗА + 5Е.
при 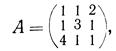 если Е—единичная матрица третьего порядка.
если Е—единичная матрица третьего порядка.
Решение
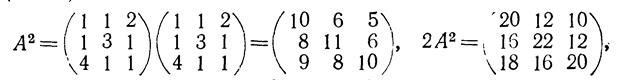
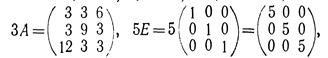
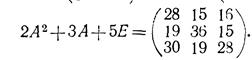
6. Дана матрица 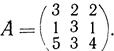 Найти обратную матрицу.
Найти обратную матрицу.
Решение
Вычисляем определитель матрицы А:
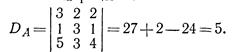
Находим алгебраические дополнения элементов этого определителя:
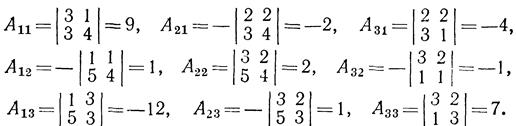
Следовательно,
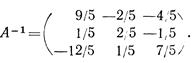
Задачи

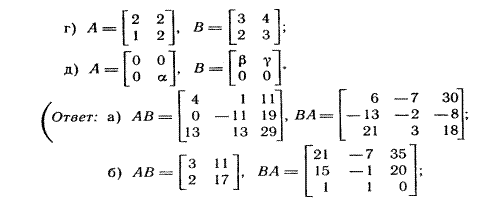

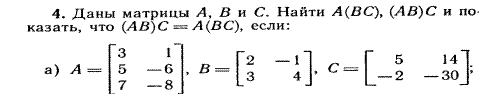
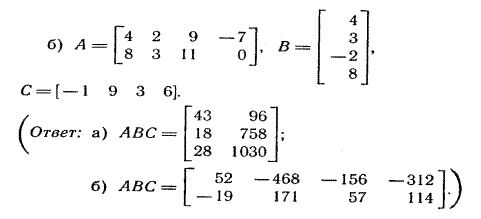
- Дана матрица
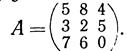 Какую матрицу В нужно прибавить к матрице А,
Какую матрицу В нужно прибавить к матрице А,
чтобы получить единичную матрицу?
- Дана матрица
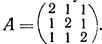 Найти сумму матриц А2 + А +Е.
Найти сумму матриц А2 + А +Е. - Дана матрица
 Найти обратную матрицу.
Найти обратную матрицу.

Индивидуальные задания

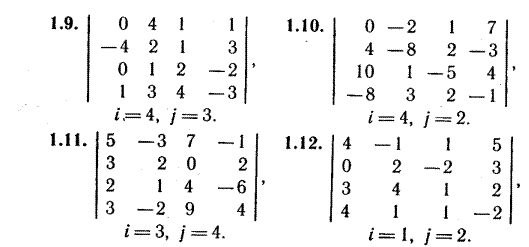

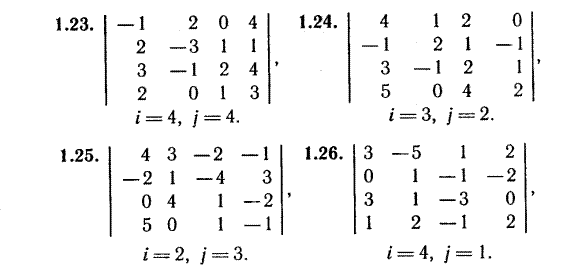

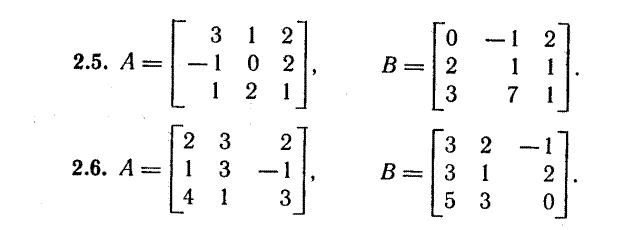
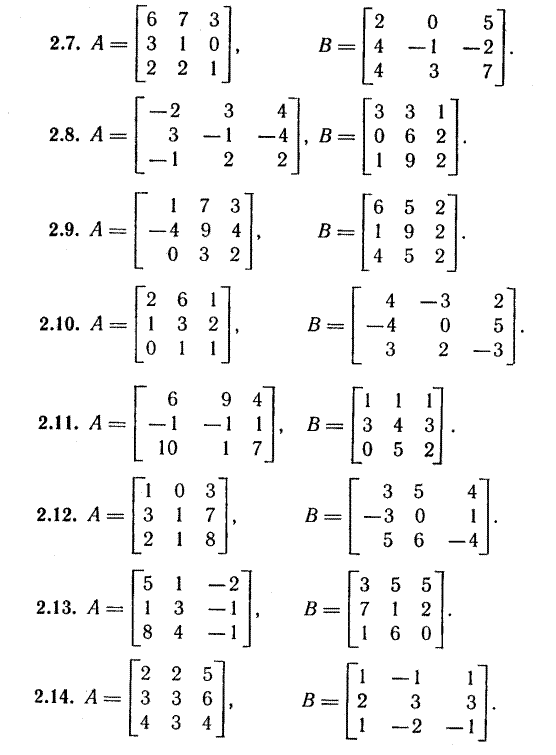
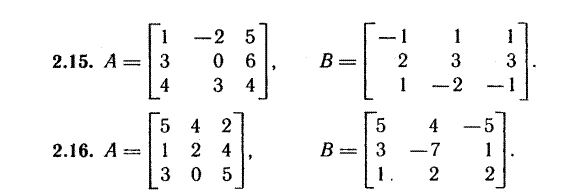
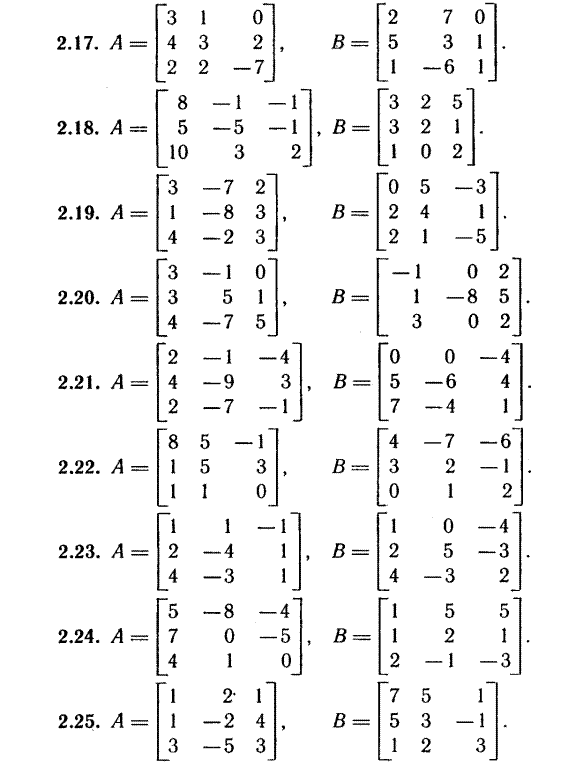
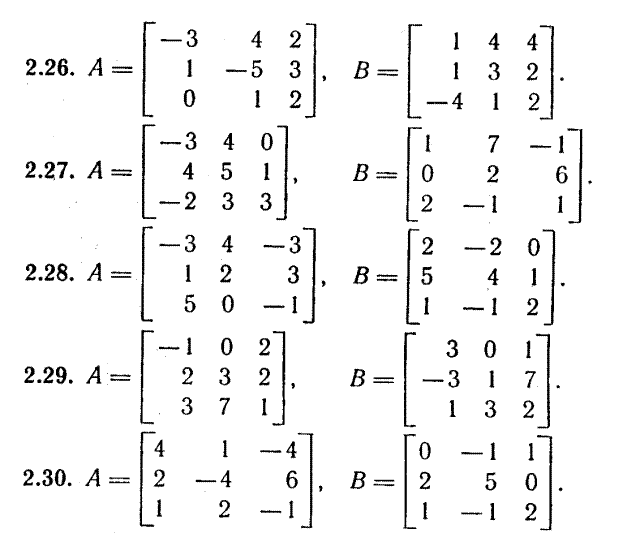
Системы линейных уравнений.
Система уравнений
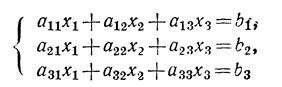
может быть записана в виде АХ = В, где
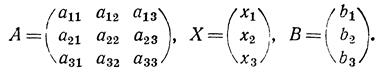
Решение этой системы имеет вид Х = А-1 В (если DА ≠ 0).
Характеристическим уравнением матрицы
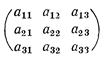
называется уравнение
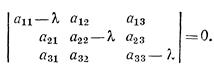
Корни этого уравнения λ1, λ2, λ3 называются характеристическими числами
матрицы; они всегда действительны, если исходная матрица является симметрической.
Система уравнений
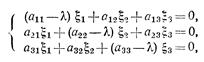
в которой λ имеет одно из значений λ1, λ2, λ3 и определитель которой в силу этого
равен нулю, определяет тройку чисел (ξ1, ξ2, ξ3) соответствующую данному
характеристическому числу.
Эта совокупность трех чисел (ξ1, ξ2, ξ3) с точностью до постоянного множителя
определяет ненулевой вектор г =ξ1i+ ξ2j+ ξ3k, называемый собственным вектором
матрицы.
Решением этой системы называется совокупность n чисел (х1, х2,..., хn) которые,
будучи подставлены вместо неизвестных в уравнения, обращают эти уравнения в
тождества. Система уравнений называется совместной, если она имеет
хотя бы одно решение (х1, х2,..., хn). Если же система не имеет ни одного решения, то
она называется несовместной.
Совместная система называется определенной, если она имеет только одно решение,
и неопределенной, если она имеет больше одного решения.
Матрицы
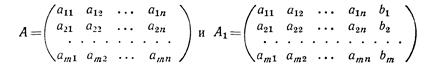
называются соответственно матрицей и расширенной матрицей системы .
Для совместности системы необходимо и достаточно, чтобы ранг матрицы
этой системы был равен рангу ее расширенной матрицы (теорема Кронекера —
Капелли). Итак, система совместна тогда и только тогда, когда г (А) = г (А1) = г.
В этом случае число г называется рангом системы .
Если b1 = b2= ... =bn = 0, то система линейных уравнений называется
однородной. Однородная система уравнений всегда совместна.
Если ранг совместной системы равен числу неизвестных (т. е. г = п), то система
является определенней.
Если же ранг совместной системы меньше числа неизвестных, то система —
неопределенная. Остановимся на последнем случае. Итак, предположим, что система
совместна, причем г < п. Рассмотрим какой-нибудь базисный минор матрицы А.
Выделим в этом миноре произвольную строку. Элементы этой строки являются
коэффициентами при г неизвестных в одном из уравнений системы . Эти г
неизвестных назовем базисными неизвестными рассматриваемой системы уравнений.
Остальные п — г неизвестных системы назовем свободными неизвестными.
Выделим из системы систему г уравнений, среди коэффициентов которых
содержатся элементы базисного минора. Базисные неизвестные в выделенной
системе оставим в левых частях уравнений, а члены, содержащие свободные
неизвестные, перенесем вправо. Из полученной системы уравнений выразим
базисные неизвестные через свободные неизвестные (например, по формулам
Крамера).
Таким образом, придавая свободным неизвестным произвольные значения,
можно найти соответствующие значения базисных неизвестных. Следовательно
(об этом уже сказано выше), система имеет бесчисленное множество решений.
Задания с решениями
- Решить систему уравнений
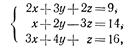
представив ее в виде матричного уравнения.
Решение Перепишем систему в виде АХ = В, где
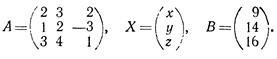
Решение матричного уравнения имеет вид X = A-1 B. Найдем A-1 . Имеем
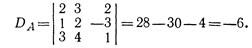
Вычислим алгебраические дополнения элементов этого определителя:
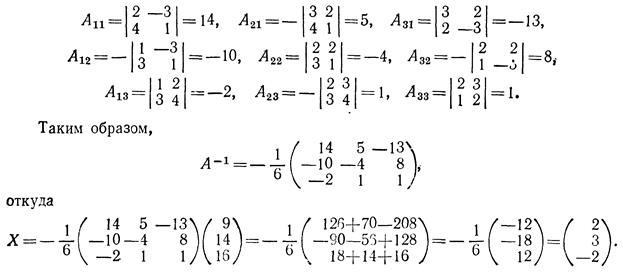
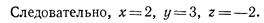
- Дана матрица
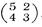
Найти ее характеристические числа и собственные векторы.
Решение Составляем характеристическое уравнение
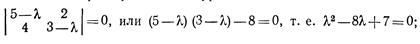

Подставив значение λ2= 7, приходим к соотношению ξ1- ξ2 = 0, т.е. ξ1= ξ2= β≠ 0.
Собственным вектором, соответствующим этому характеристическому числу, служит r2 = βi + βj
- Найти характеристические числа и собственные векторы матрицы
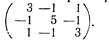
Решение Составляем характеристическое уравнение

Итак, собственные векторы заданной матрицы имеют вид r1 = α(i— k); г2 = β(i + j +к); г3 = γ(i — 2j —k), гдеα,β, γ — произвольные отличные от нуля числа,
- Исследовать систему уравнений
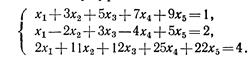
Решение Определим ранги матрицы и расширенной матрицы системы. Выпишем
расширенную матрицу
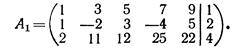

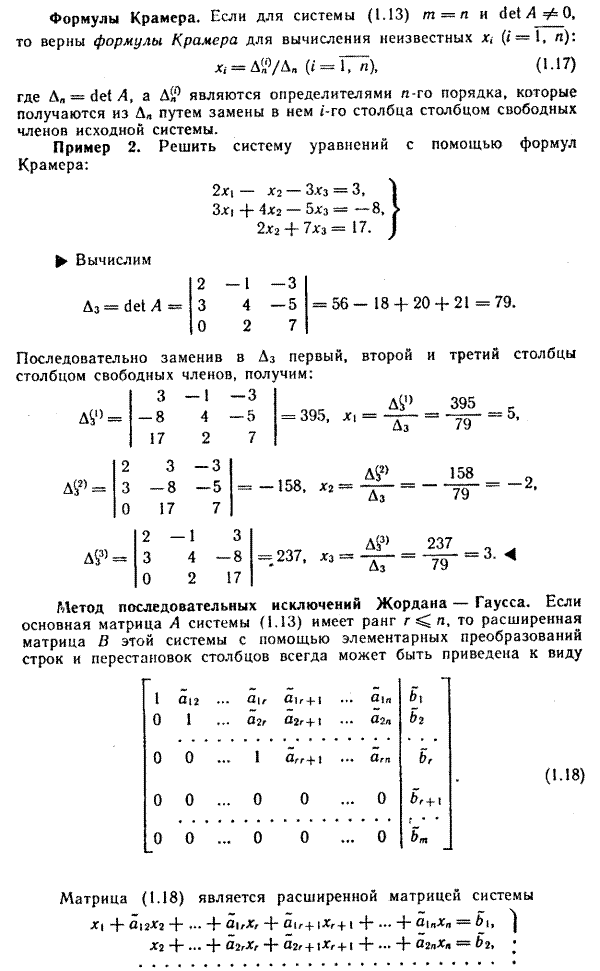

Задачи


5. Решить систему уравнений
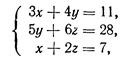
представив ее в виде матричного уравнения.
6. Найти характеристические числа и нормированные собственные векторы матрицы
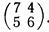
7. Найти характеристические числа и собственные векторы матрицы
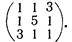
Решить системы уравнений
8 13
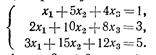
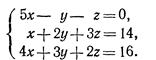
9 14
10 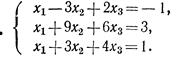 15
15 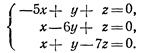
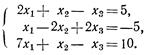
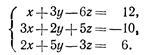
11 16
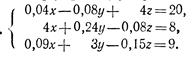
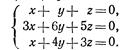
12 17
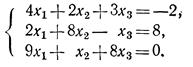
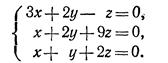

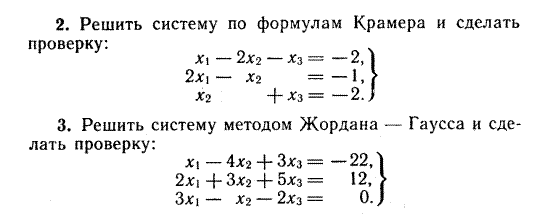
Индивидуальные задания