Уравнение теплопередачи излучением

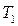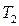Теплообмен между двумя поверхностями, нагретыми до температур и при преобладании теплопередачи излучением в соответствие с законом Стефана – Больцмана описывается уравнением

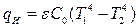(3.87)

где 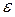– приведенная степень черноты;

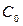– коэффициент лучеиспускания абсолютно черного тела.

Чаще всего передача тепла теплопроводностью, конвекцией и излучением наблюдается одновременно. В этом случае пользуются общим коэффициентом теплоотдачи, представляя тепловой поток в виде

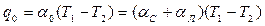(3.88)

где 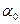– общий коэффициент теплоотдачи;

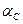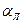и – коэффициенты теплоотдачи соприкосновением и лучеиспусканием.

В ряде случаев, особенно при большой доли теплопередачи излучением, лучшие результаты может дать уравнение по структуре аналогичное (3.87)

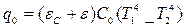
Допущения (постулаты) в методе наименьших квадратов ----------------

Метод наименьших квадратов, положенный в основу определения коэффициентов уравнения регрессии, может дать раздельные несмещенные (достоверные) оценки коэффициентов b0,b1,2…лишь при соблюдении определенных предпосылок (допущений), которые часто трудновыполнимы.

Главнейшими из них являются следующие:

а) входные величины x1,x2….xk(теоретически неслучайные) должны измеряться с точностью значительно превышающей точность измерения выходной величины ;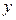

б) входные величины x1,x2….xkне должны быть коррелированны, т. е. статистически связаны между собой. Это условие весьма трудно соблюсти на практике. Например, из соображений управления процессом часто требуется одновременно согласованное изменение нескольких управляющих воздействий;

в) выходной параметр yесть случайная величина, подчиняющаяся нормальному закону распределения;

г) рассеяние (дисперсия) выходного параметра yне зависит от его абсолютной величины (условие равноточности опытов).

25----------- Кодирование переменных и условия ортогональности при планировании эксперимента типа ПФЭ-2^{К---------------------}

Для определения уравнения регрессии линейного вида (5.17), входные переменные, которые будем называть в дальнейшем варьируемыми факторами, поддерживаются в этом случае на двух заранее выбранных фиксированных уровнях. Верхний уровень 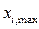кодируется через +1, нижний 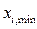через -1. Соотношение между натуральными и кодированными переменными имеет вид

,

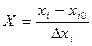где 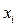– натуральная переменная;

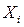– кодированная переменная, принимающая значения +1 или -1;

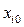– средний (нулевой) уровень, около которого осуществляется варьирование;

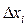– интервал (шаг) варьирования по отношению к .

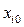Число опытов определяется из соотношения

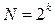, где 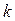– число варьируемых факторов.

Благодаря переходу к кодированным переменным, которые принимают лишь два значения (-1) (+1), и специальному планированию экспериментов автоматически выполняется весьма важное условие статистической независимости варьируемых факторов (условие ортогональности)

;

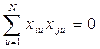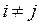
т. е. выполняется одна из важнейших предпосылок регрессионного анализа.

26-------Формулы для определения коэффициентов уравнения регрессии при эксперименте типа ПФЭ-2^{К-------------------------}

при полном факторном эксперименте имеется возможность определить коэффициенты не только для уравнения регрессии линейного вида (5.17)

,

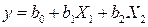но и для уравнения, отражающего взаимодействия факторов, например

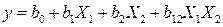, (5.22)

в случае эксперимента 2² или

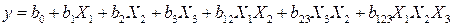(5.23)

для эксперимента 2³ и аналогично для большего числа факторов.

Критерий равноточности и опытов ---------------

Проверяют воспроизводимость опытов по критерию Кохрена

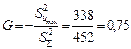(5.30)

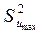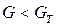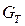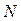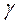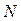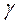где – максимальная из построчных дисперсий.Опыты равноточны, если , где – табличное значение критерия Кохрена, выбираемое в зависимости от , и уровня значимости (надежности). Для данного случая при =4, =2, 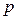=0,95 табличное значение 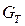= 0,906, т. е. 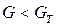. В случае неравноточности опытов необходимо увеличить число повторных экспериментов или повысить их точность.

Критерий адекватности Фишера ------------

Проверяют адекватность (пригодность) модели, т. е. насколько хорошо полученное уравнение описывает результаты эксперимента в исследуемой области.

Для этого чаще всего применяют критерий Фишера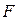

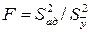(5.35)

где 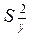– усредненная дисперсия эксперимента, определяемая по формуле (178);

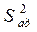– дисперсия адекватности или остаточная дисперсия;

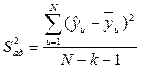
29 формула для расчёта АКФ

где х_t - значение времени прихода текущей единицы;

х_t-k - значение времени прихода единицы, сдвинутой на r интервалов назад;

где n - объем выборки, а m - количество вариантов.

Формула для расчета вкф-------------