Примеры неустойчивости алгоритмов

Пример 1.4. Вычисление экспоненты с помощью ряда Маклорена:

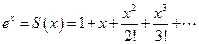. (1.1)

Как известно, этот ряд сходится на всей числовой оси, однако, при использовании реальных систем представления чисел могут возникнуть ошибки. Рассмотрим вычисления в десятичной системе с длиной мантиссы t=4. Система с усечением: остальные разряды просто отбрасываются.

Найдем 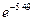. Суммирование закончим, как только абсолютная величина очередного слагаемого станет меньше, чем 0.0001 от суммы ряда. Дальнейшее суммирование бессмысленно. В данном случае в сумме оказывается 25 слагаемых. Выпишем несколько слагаемых:

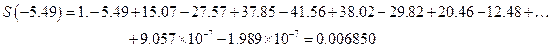
Истинное значение 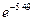равно 0.004128. Имеем катастрофическую потерю верных знаков! Ошибка связана с тем, что наибольшие слагаемые по абсолютной величине на несколько порядков больше конечной суммы. Погрешность округления для этих слагаемых сравнима с окончательным результатом. К тому же ряд является знакопеременным. При вычитании чисел возрастает относительная ошибка. Например, алгебраическая сумма двух наибольших слагаемых ряда равна 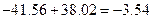. Полагаем, что абсолютная погрешность равна примерно половине отброшенного разряда. Следовательно, относительная погрешность для вычитаемых чисел имеет порядок 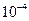, а для разности эта погрешность на порядок выше (учитывая, что при вычитании абсолютные погрешности могут как вычитаться, так и складываться).

Если слегка изменить значение x, получим вообще парадоксальный результат: значение экспоненты 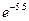равно 0.004087, в то время как сумма ряда в нашей системе оказывается отрицательной .

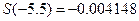Видим, что алгоритм непосредственного суммирования ряда (1.1) в нашей системе оказывается неустойчивым. Однако алгоритм может быть легко улучшен. Чтобы избежать потери точности при вычитании, вычислим 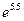и найдем обратную величину 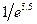. В этом случае вычисления с помощью ряда Маклорена дают неплохой результат:

.

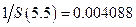Пример Уилкинсона

Пример Уилкинсона – это пример неустойчивой задачи, в которой незначительное изменение входных параметров приводит к принципиальному изменению решения.

Пример 1.5.

Введем многочлен двадцатой степени:

.

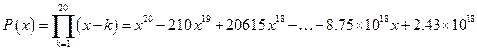Корнями многочлена 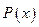, естественно, являются натуральные числа от 1 до 20.

Введем небольшое изменение в многочлен 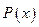: изменим слегка коэффициент при 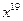. Пусть новый многочлен равен 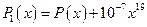. Корни многочлена 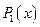, вычисленные с помощью пакета Mathematica, приведены в таблице.

Корни многочлена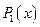

1.	6.00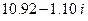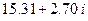
2.	7.00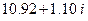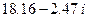
3.	7.99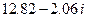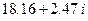
4.	9.11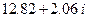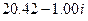
5.	9.57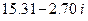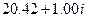

Видим, что незначительное изменение одного из коэффициентов многочлена привело к появлению комплексных корней. Исследуем причину этого явления. Обозначим коэффициент многочлена при 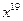буквой 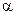и найдем зависимость корней многочлена от этого коэффициента. Для этого будем рассматривать наш многочлен как функцию двух аргументов 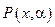. Продифференцируем по 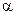уравнение 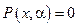, полагая 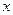функцией :

.

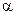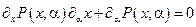Найдем отсюда производную :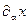

.

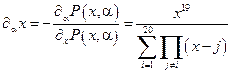При x = k эта производная равна

.

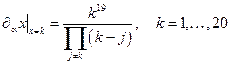Результаты расчетов по этой формуле представлены в таблице.

Значения производной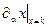

k	Значение производной	k	Значение производной	k	Значение производной	k	Значение производной

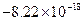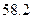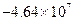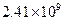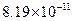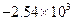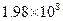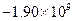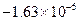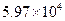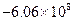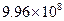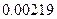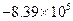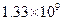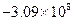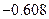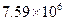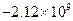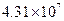Видим, что имеет место резкая зависимость корней многочлена от значения коэффициента при x¹⁹.

Пример 1.6.

Рассмотрим более простой пример. Будем искать корни многочлена четвертой степени, используя средства пакета Mathematica.. Сохраним нотацию пакета Mathematica. Входные выражения (In[ ] :=) содержат команды, выходные – (Out[ ] =) включают результаты вычислений.

Определим многочлен четвертой степени:

In[ ] := P[x_] = Expand[ Product[(x-k), {k, 4}] ]Out[ ] =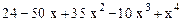

Слегка изменим коэффициент при x³ и найдем корни полученного многочлена с помощью функции Solve:

In[ ] := Solve[ P[x] + 0.03 x^3 == 0 ]

Out[ ] =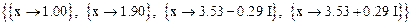

Отметим, что корни многочлена P[x] – натуральные числа от 1 до 4; относительно небольшое изменение коэффициента при x³ (на 0,3%) приводит к появлению комплексных корней. Следовательно, решение уравнения четвертой степени также является неустойчивой задачей.

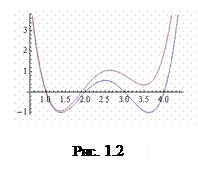
График на рисунке 1.2 поясняет возникающий эффект. Изменение коэффициента приводит к тому, что новый многочлен имеет только два действительных корня.

Вопросы для повторения

1. Почему могут возникнуть погрешности при переводе числа из одной системы счисления в другую?

2. Какими параметрами характеризуется представление чисел в системах с плавающей запятой?

3. Что называется абсолютной и относительной погрешностью приближенного значения числа?

4. Какое требование предъявляется к оценкам погрешности приближенного значения числа?

5. Что называется машинным эпсилоном? Что характеризует машинный эпсилон?

6. Какой величиной оценивается абсолютная погрешность дифференцируемой функции 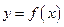, вызываемая достаточно малой погрешностью аргумента ?

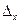7. Какой величиной оценивается абсолютная погрешность дифференцируемой функции 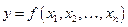, вызываемая достаточно малыми погрешностями 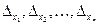аргументов?

8. Как оценивается абсолютная погрешность алгебраической суммы нескольких приближенных чисел?

9. Почему относительная погрешность разности двух чисел одного знака больше относительной погрешности этих чисел?

10. Какие алгоритмы называются неустойчивыми? Почему такие алгоритмы непригодны для вычислений?