Выявление и характеристика основной тенденции развития
Выявление общей тенденции изменения динамического ряда обеспечивается при помощи особых приемов. Наиболее простым способом является укрупнение интервалов и определение итога уровня для этих интервалов или исчисление средних для каждого укрупненного интервала. При этом используют либо переменную среднюю, либо скользящую среднюю. Исчисление итогов за укрупненный период возможно только по интервальным рядам абсолютных величин. Во всех других случаях следует исчислять среднюю величину уровня в укрупненном интервале.
При использовании переменной средней укрупнение интервала обычно начинают с наименьшего возможного, т.е. с интервала, объединяющего два периода. Если в этом случае тенденция развития четко не проявляется, переходят к следующему возможному интервалу, объединяющему три периода. Недостатком этого способа является то, что из поля зрения исследователя выпадает процесс изменения внутри укрупненного интервала, что вызвано сокращением числа уровней изучаемого ряда. Однако преимуществом является сохранение экономической природы явления.
Расчет переменной средней осуществляется по формулам средней арифметической. Например, если укрупненный интервал образован объединением трех периодов, средние для укрупненных интервалов определяются следующим образом:
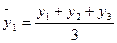 ;
; 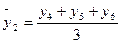 и т.д., (7.2)
и т.д., (7.2)
где 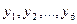 - уровни исходного ряда динамики.
- уровни исходного ряда динамики.
Скользящая средняя – подвижная динамическая средняя, которая исчисляется по ряду при последовательном передвижении на один интервал, т.е. сначала вычисляют средний уровень из определенного числа первых по порядку уровней ряда, затем – средний уровень из такого же числа членов, начиная со второго. Если в ряду динамики имеются периодические колебания, то период скользящей средней должен совпадать с периодом колебания или быть кратным ему. Если в ряду периодических колебаний нет, то период скользящей подбирают, начиная с наименьшего (т.е. с двух уровней), если в этом случае тенденция не проявляется, то период укрупняют. Период скользящей может быть четным и нечетным; практически удобнее использовать нечетный период, т.к. в этом случае скользящая средняя будет отнесена к середине периода скольжения.
Например, скользящие средние с продолжительностью периода, равной 3, следующие:
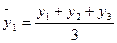 ;
; 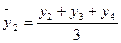 ;
; 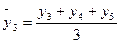 и т.д. (7.3)
и т.д. (7.3)
Полученные средние записываются к соответствующему срединному интервалу (второму, третьему, четвертому и т.д.).
Если период скользящей четный, то выполняют центрирование данных, т.е. определение средней из найденных средних, что необходимо для определения срединного периода. Например, если исчисляется скользящая с продолжительностью периода, равной 2, то расчет производится следующим образом:
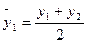 ;
; 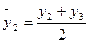 ;
; 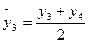 и т.д. (7.4)
и т.д. (7.4)
Тогда центрированные средние равны:
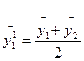 ;
; 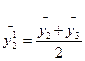 и т.д. (7.5)
и т.д. (7.5)
Первая центрированная средняя будет отнесена ко второму периоду, вторая – к третьему и т.д.
Сглаженный ряд «укорачивается» по сравнению с фактическим на 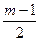 члена с одного и другого конца, где m – количество уровней, входящих в интервал.
члена с одного и другого конца, где m – количество уровней, входящих в интервал.
Рассмотренные приемы не позволяют получить описание плавной линии развития (тренда) данного динамического ряда. Для этой цели используется аналитическое выравнивание, сущность которого заключается в нахождении уравнения, выражающего закономерность изменения явления как функцию времени 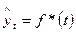 .
.
Вид уравнения определяется характером динамики развития конкретного явления. Логический анализ при выборе вида уравнения может быть основан на рассчитанных показателях динамики, а именно:
- если относительно стабильны абсолютные приросты (первые разности уровней приблизительно равны), сглаживание может быть выполнено по прямой;
- если абсолютные приросты равномерно увеличиваются (вторые разности уровней приблизительно равны), можно принять параболу второго порядка;
- при ускоренно возрастающих (замедляющихся) абсолютных приростах – параболу третьего порядка;
- при относительно стабильных темпах роста – показательную функцию.
На практике выбор кривой может быть основан на анализе графического изображения уровне динамического ряда (линейной диаграммы); при этом целесообразнее воспользоваться графическим изображением сглаженных уровней, в которых случайные колебания погашены. Если условия формирования уровней ряда изменяются, то расчет параметров уравнения не следует вести по данным за весь рассматриваемый период. В этом случае целесообразно разбить ряд динамики на ряд периодов, основываясь на оценке устойчивости показателей динамики.
В таблице 7.3 приводятся различные виды трендовых моделей, наиболее часто используемых для аналитического выравнивания.
Таблица 7.3 - Виды трендовых моделей
| № п/п | Наименование функции | Вид функции | Система нормальных уравнений для нахождения параметров уравнения |
| 1. | Линейная | 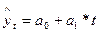 | 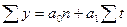  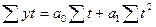 |
| 2. | Парабола второго порядка | 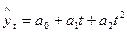 | 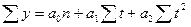 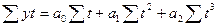 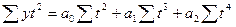 |
| 3. | Показательная | 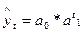 | 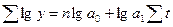 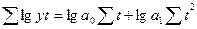 |
| 4. | Гиперболическая | 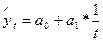 | 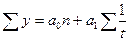 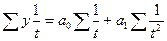 |
Вычислительный процесс нахождения параметров уравнения при сохранении полной идентичности конечных результатов может быть значительно упрощен, если ввести обозначения дат (периодов) времени с помощью натуральных чисел (t), с тем, чтобы t = 0.
Так, если количество уровней в ряду динамики нечетные, то временные даты (t) обозначаются следующим образом:
| Временные даты (периоды) | Январь | Февраль | Март | Апрель | Май |
| Уровни ряда динамики | 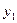 | 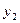 | 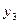 | 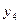 | 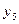 |
| Обозначения временных дат (t) | -2 | -1 | +1 | +2 |
Если же количество уровней в ряду динамики четное, то обозначения временных дат дат (t) принимают следующий вид:
| Временные даты (периоды) | Январь | Февраль | Март | Апрель | Май | Июнь |
| Уровни ряда динамики | 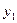 | 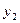 | 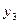 | 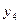 | 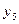 | 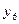 |
| Обозначения временных дат (t) | -5 | -3 | -1 | +1 | +3 | +5 |
Тогда система нормальных уравнений при выравнивании по прямой примет вид:
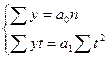 . (7.6)
. (7.6)
Откуда 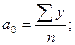
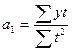 . (7.7)
. (7.7)
Расчет сумм слагаемых целесообразно вести в таблице. Например, при выравнивании по показательной функции вид таблицы следующий:
| Дата | Уровни ряда динамики | Обозначения временных дат | 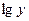 | 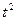 | 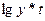 | 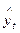 |
| . . . | ||||||
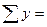 | 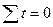 | 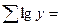 | 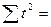 | 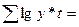 | 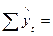 |
По полученной модели для каждого периода (каждой даты) определяются теоретические уровни тренда ( 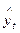 ) и стандартная ошибка аппроксимации (среднее квадратическое отклонение тренда) по формуле:
) и стандартная ошибка аппроксимации (среднее квадратическое отклонение тренда) по формуле:
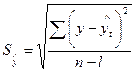 , (7.8)
, (7.8)
где 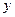 и
и 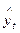 - соответственно фактические и расчетные значения динамического ряда;
- соответственно фактические и расчетные значения динамического ряда;
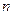 - число уровней ряда;
- число уровней ряда;
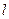 - число параметров в уравнении тренда.
- число параметров в уравнении тренда.
При составлении прогнозов уровней социально-экономических явлений обычно оперируют не точечной, а интервальной оценкой, рассчитывая так называемые доверительные интервалы прогноза. Границы интервалов определяются по формуле:
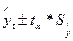 , (7.9)
, (7.9)
где 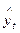 - точечный прогноз, рассчитанный по модели;
- точечный прогноз, рассчитанный по модели;
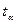 - коэффициент доверия по распределению Стьюдента при уровне значимости
- коэффициент доверия по распределению Стьюдента при уровне значимости 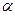 .
.
